地铁车站轨排井扶壁柱控制弯矩理论计算与讨论
2020-08-27刘小华
刘小华, 黎 莹
(1.广州地铁设计研究院股份有限公司, 广东 广州 510010;2.西安交通大学 城市学院, 陕西 西安 710018)
在地铁建设过程中,为了便于轨道高效便捷地铺设,通常将两根钢轨在地面并排组装成轨排后,吊装至地铁车站内部用于线路铺设,从而需要在车站的主体结构板上预留轨排吊装的洞口,该洞口被称为轨排井。钢轨每节的长度一般为25 m,为满足轨排安全、高效吊装的要求,轨排井常开设于地铁线路正上方,洞口净尺寸长约27 m~30 m,宽度约为3.5 m~5.0 m,洞口个数根据排轨吊装需要确定[1]。
车站主体结构开设轨排井后,轨排井范围的车站侧墙失去结构板的支撑成为车站的薄弱部位。为了抵御侧墙外侧强大的水土压力,提高结构平面外刚度,保证结构安全及正常使用功能,在板洞边设置边框梁与侧墙设置扶壁柱组合的结构形式在地铁设计中广泛采用[2-7]。轨排井中部扶壁柱柱底弯矩是扶壁柱设计的控制弯矩[7],直接影响到扶壁柱截面尺寸及配筋面积。在实际工程中虽已有应用,但往往存在两种极端倾向:单纯地为了轨排吊装的便利性而将轨排井洞口设置贴近侧墙,边框梁高度受限刚度较弱,导致扶壁柱截面及配筋巨大造成浪费;或者为了保证侧墙能获得有效支撑而将轨排井远离侧墙设置,忽略吊装的便利性。究其原因,由于扶壁柱柱底控制弯矩与轨排井位置关系的理论研究成果非常有限,设计人员缺乏相关理论研究作为指导,对扶壁柱控制弯矩与轨排井位置关系间的规律有一定的定性认识,但缺乏定量认识,在设计选型上存在一定的盲目性,难以兼顾轨排井使用便利性与结构设计的安全经济性(见图1)。

图1 地铁车站轨排井实景图
本文拟在适当假定的前提下,抽象出轨排井扶壁柱控制弯矩计算简图,分析推导出扶壁柱在水土压力等荷载作用下柱底控制弯矩近似解析解,通过二维有限元模拟验证推导公式的正确性,采用三维整体模型分析进一步证明假定的合理性及解析解的工程适用性。在深入分析结构受力机理后,利用解析解得到扶壁柱控制弯矩对轨排井位置(实质为扶壁柱与边框梁刚度比)变化的敏感区域,有助于设计人员在敏感区内确定合理柱梁刚度比,取得轨排井使用便利性与结构安全经济性间的平衡。
1 模型假定与计算推导
1.1 模型假定
扶壁柱加边框梁式轨排井中部扶壁柱柱底弯矩是结构设计的控制弯矩,是计算结构尺寸及配筋的必要条件。快速准确地获取柱底控制弯矩对结构设计至关重要。根据地铁车站实际功能需求,两层层高通常相差不大,为了便于分析推导,作如下简化假定:
(1) 忽略墙厚的影响。
(2) 假定上下两层边框梁截面相同。
(3) 假定车站上下两层层高相同。
(4) 假定扶壁柱与车站底板,边框梁与端侧墙刚接。
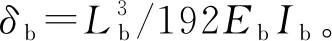

图2 扶壁柱计算模型简化图
1.2 柱底控制弯矩推导
埋置于地下的地铁车站侧墙主要受到土压力、水压力以及地面车辆荷载引起的侧向土压力等荷载[8-12],合力通常为梯形分布荷载(见图3、图4)。轨排井中部扶壁柱柱底弯矩的求解问题可以简化为在任意梯形分布荷载作用下柱底端固支,中部及顶端在弹性支座支撑下的力学问题。
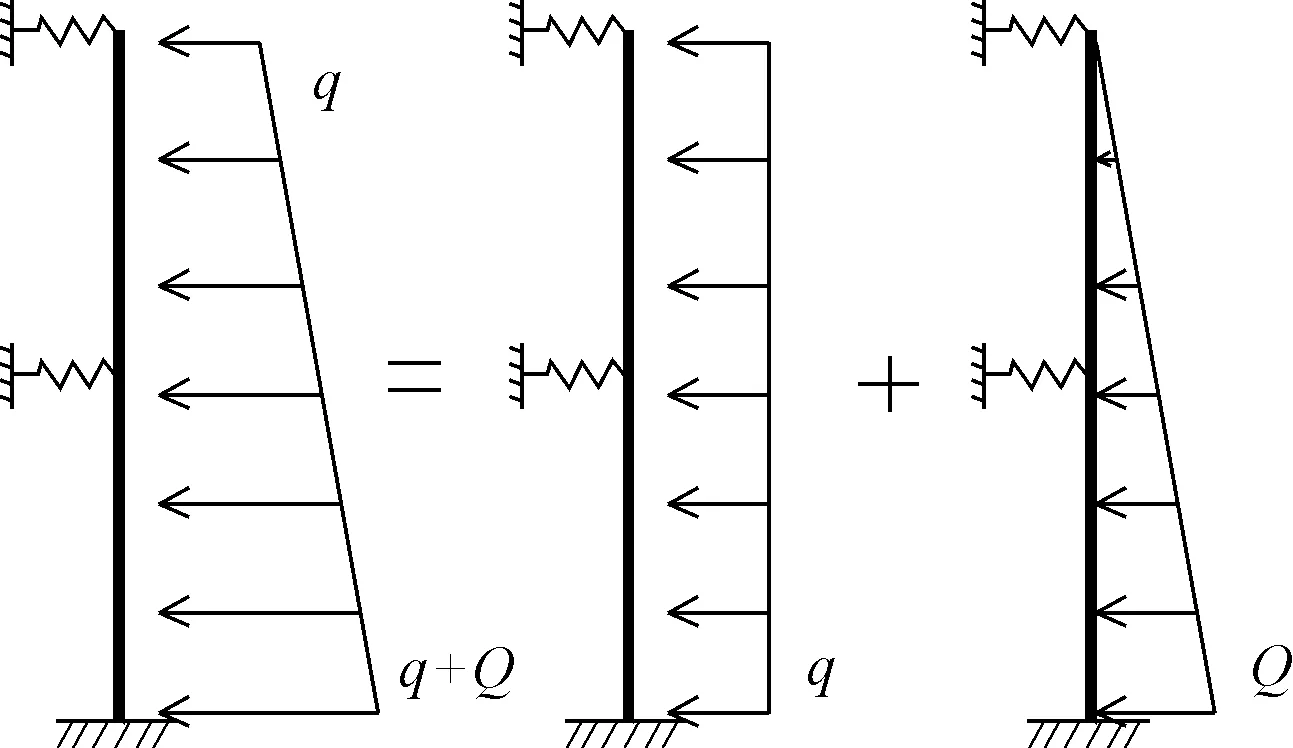
图3 扶壁柱计算模型分解图

图4 均布荷载作用下力法基本体系图
构件在弹性阶段,内力满足线性叠加原理[13]。在梯形分布荷载作用下,可分解为在均布荷载与三角形荷载单独作用下的内力和。
在均布荷载作用下,把图4中顶端及中部的弹簧支座去掉,分别以多余未知力X1,X2取而代之,这样将超静定结构转化为含多余未知力X1,X2的静定结构,得到构件在均布荷载作用下力法基本体系图(见图5)。基本体系与原超静定结构等价的条件是:在X2及q的作用下,顶端弹性支座的位移与原超静定结构在q作用下相同,且在X1及q的作用下,中部弹性支座的位移与原超静定结构在q作用下相同。由此得到其力法基本方程[14]为:
(1)
(2)
其中:X1,X2分别为顶端和中部弹性支座作用于柱的反力;Δ1p为基本体系下外力q单独作用时顶端沿X1方向的位移;Δ2p为基本体系下外力q单独作用时中部沿X2方向的位移;δ11为基本体系下单位力单独作用于顶端时沿X1方向的位移;δ22为基本体系下单位力单独作用于中部时沿X2方向的位移;δ12为基本体系下单位力单独作用于中部时沿X1方向的位移;δ21与δ12类似。
由图乘法得:
(3)
(4)
式中:E为扶壁柱的弹性模量;I为扶壁柱的截面惯性矩;L为扶壁柱的计算长度。


代入上式(1)和式(2)解得,
(5)
(6)
柱底控制截面弯矩为:
(7)
(8)

将X1,X2代入式(7)整理得到在均布荷载作用下柱底控制截面弯矩解析解为:
(9)
在三角形荷载Q作用下,力法基本体系与均布荷载作用下的基本体系相同,仅外荷载不同,同理可得,
(10)
(11)
δ11、δ22、δ12及δ21与均布荷载作用下含义及值均相同,可见式(3)。
将式(10)及式(11)代入式(1)和式(2)解得,在三角形荷载Q作用下顶端和中部弹性支座作用于柱的反力分别为:
(12)
(13)
代入式(7)整理得到在三角形荷载作用下柱底控制截面弯矩解析解为:
(14)
令β=Q/q,则在均布荷载和三角形荷载共同作用下,弯矩线性叠加得柱底控制截面弯矩解析解为:
M=
(15)
2 模型验证
2.1 模型基本参数
以洛阳地铁二号线已建成的某车站为例,车站设置轨排井一处,洞口尺寸为5 m×28 m,扶壁柱截面尺寸为600 mm×1 800 mm,柱平面布置中心间距3 m,采用C50混凝土,上下层边框梁均为800 mm×1 850 mm,侧墙厚度为600 mm,采用C35混凝土,顶板覆土1.5 m,主动土压力系数按0.38考虑,地下水位于底板以下,考虑地面车辆荷载20 kPa,土重度均按20 kN/m3考虑,其他参数如图5、图6所示。

图5 轨排井平面图(单位:mm)

图6 轨排井剖面图(单位:mm)
2.2 二维模型验证
采用有限元软件MIDAS/Gen建立二维模型,边框梁和扶壁柱均用梁单元模拟[15],柱底施加固定约束。图7(a)给出了带边框梁的扶壁柱模型(梁两端固结,柱底固结,施加梯形荷载);图7(b)—图7(d)为设弹性支座的扶壁柱模型,将中部和顶部梁简化为弹性支座,支座刚度按本文公式推导取值,柱底固结,其中图7(b)施加梯形荷载、图7(c)仅施加均布荷载、图7(d)仅施加三角形荷载。图8(a)—图8(d)给出了对应模型下的弯矩的计算结果。

图7 二维计算模型图(单位:kN/m)

图8 二维计算扶壁柱弯矩图(单位:kN·m)
表1列出了根据本文推导的解析解得出的各种工况下的柱底控制弯矩及重要参数。扶壁柱间距为3 m,取3 m范围侧向压力换算成线荷载作用于扶壁柱上。
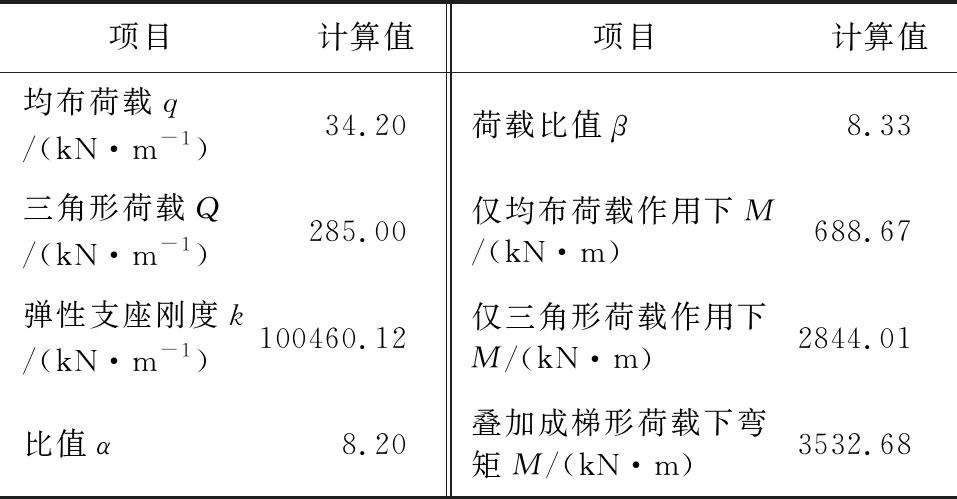
表1 解析解计算表
由图8(a)及图8(b)可知,将梁简化为弹性支座后二者在相同荷载作用下,柱底弯矩几乎相等,说明将梁等效为弹性支座是合理可行的,同时也验证本文推导的支座刚度的正确性。结合表1的结果及图8可知,扶壁柱柱底控制弯矩解析解与有限元软件计算结果一致,由此可验证本文推导的扶壁柱柱底控制弯矩解析解的正确性。
2.3 三维模型检验
采用有限元软件MIDAS/Gen建立三维整体模型,边框梁和扶壁柱均用梁单元模拟,墙采用壳单元模拟。模型基本参数按2.1节。不考虑围护结构对车站主体结构的影响。三维计算整体变形图及扶壁柱弯矩图分别如图9、图10所示。
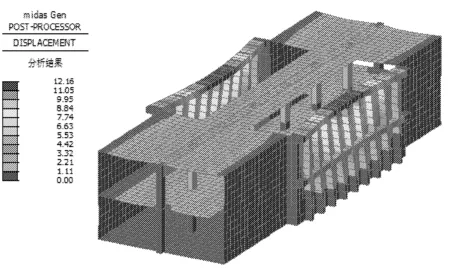
图9 三维计算整体变形图(单位:mm)
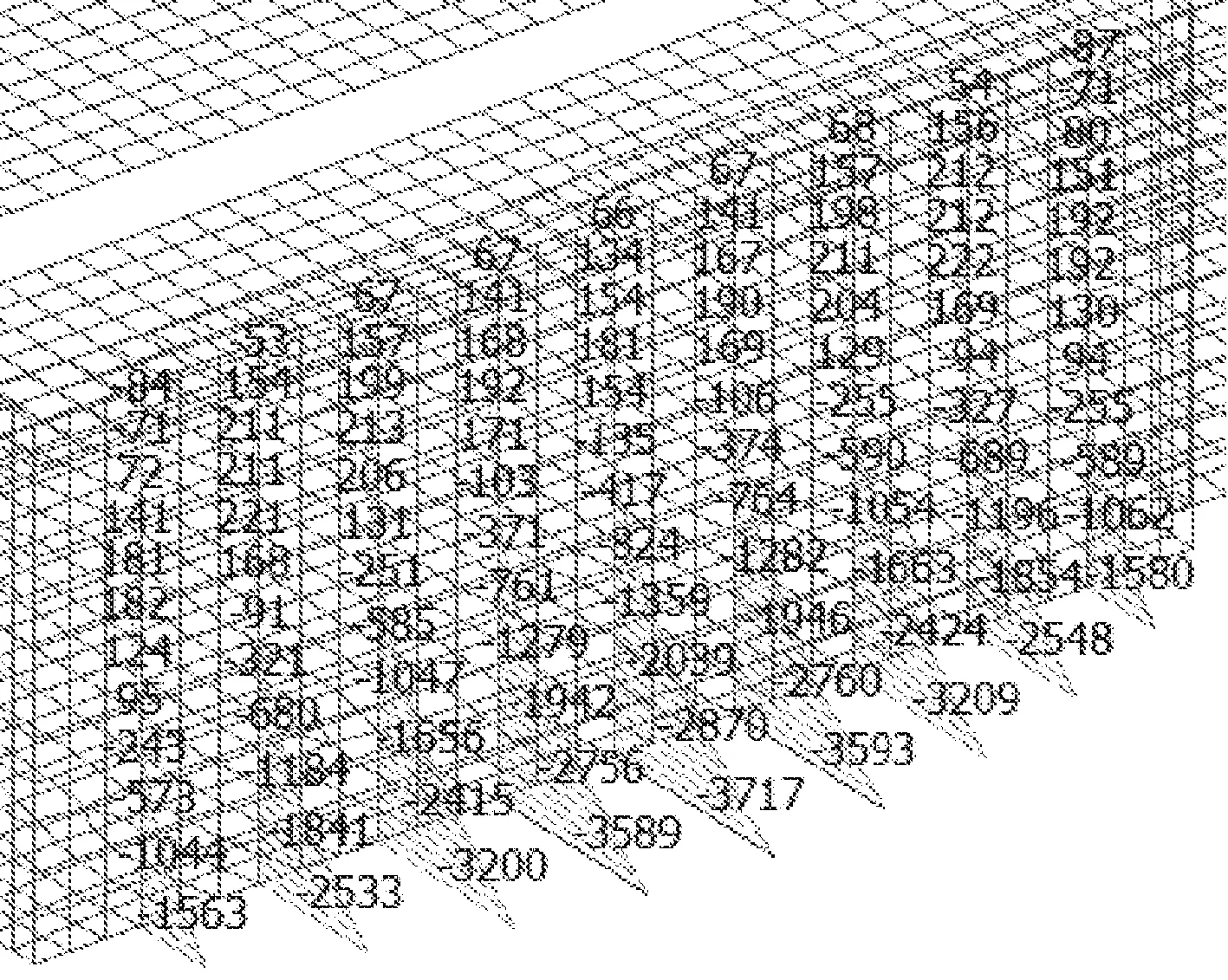
图10 三维计算扶壁柱弯矩图(单位:kN·m)
由整体变形图9可知,第一道边框梁变形明显大于中部边框梁,轨排井洞口中部扶壁柱变形最大,变形依次向两边递减,轨排井侧墙整体呈现出类似三边固结顶边自由板的变形特征。从图10可知,中部扶壁柱柱底弯矩最大(3 717 kN·m),为扶壁柱控制弯矩。根据本文推导的解析解计算,扶壁柱柱底控制弯矩为3 533 kN·m,二者误差为-4.95%,结果吻合性较好,误差在工程允许范围内,由此验证了扶壁柱控制弯矩解析解计算简化假定的合理性,也进一步说明解析解对这类实际工程问题具有较好的适用性,尤其在初步设计阶段可以快速确定合理的梁柱截面尺寸,能避免复杂三维模型繁琐的建模与分析,大幅提高工作效率。出现解析解略小于三维整体算结果的主要原因是,边框梁两端侧墙及端柱对其转动约束有限,难以实现计算假定的绝对刚接,从而导致解析模型中弹性支座对扶壁柱的支撑刚度比实际边框梁的支撑刚度略大,进而引起扶壁柱柱底弯矩比实际柱底弯矩略小。
3 讨 论


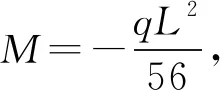
(3) 以2.1节参数为例,取β=0代入不同α值,得到扶壁柱柱底弯矩与柱梁刚度比的关系图,如图11所示。

图11 柱底弯矩与柱梁刚度比关系图
由图11可知,扶壁柱柱底弯矩对柱梁刚度比α的敏感区域为1~64,扶壁柱柱底弯矩随着柱梁刚度比的减小而显著减小,当柱梁刚度比α超出此区域,柱底弯矩变化并不明显。从而可知,在满足功能需求的情况下轨排井洞口稍靠近中纵梁,增大边框梁刚度有利于明显改善扶壁柱柱底弯矩集中的情况。而过于靠近中纵梁,牺牲轨排吊装的便利性并不能带来结构受力性能的显著改善。根据具体车站的情况,设计人员可以通过解析解在敏感区域内确定合理柱梁刚度比,取得使用便利性与结构受力性能间的平衡。以2.1节洛阳某车站为例,当轨排井洞边距离车站侧墙外壁为3 m时,柱梁刚度比α=1.92,柱底弯矩为131.3 kN·m,相比原设计距离为1.85 m(α=8.2,M=229.5 kN·m),柱底弯矩降幅达42.8%。可见清晰认识扶壁柱控制弯矩与轨排井位置关系间的规律,是合理设计的必要前提,对改善结构受力性能,节省工程造价具有重要现实意义。
(4) 需要指出的是,地铁车站功能需求决定车站层高为5.5 m~7.0 m,标准轨节长度决定轨排井洞口长度为27 m~30 m,洞口范围侧墙长高比通常大于2,因此带轨排井的双层车站侧墙中部具有类似于单向板的特性,文中的模型简化才得以成立,吻合度较好。在设计参考中应注意这一隐含条件满足与否,其直接影响解析解的准确性。
4 结 语
地铁车站开设轨排井处是车站结构的薄弱部位,是实际工程设计工作中的重难点。由于轨排井扶壁柱柱底控制弯矩与轨排井位置关系的理论研究成果非常有限,现有的设计大多难以兼顾轨排井使用便利性与结构设计的安全经济性。本文在适当假定的前提下,抽象出了轨排井扶壁柱柱底控制弯矩计算简图,分析推导了扶壁柱在水土压力等荷载作用下柱底控制弯矩近似解析解,通过二维有限元模拟验证了推导解析解公式的正确性,并进一步地采用三维整体模型分析证明了假定的合理性及解析解的工程适用性。同时,利用解析解公式找到了扶壁柱柱底弯矩对轨排井位置变化(即扶壁柱与边框梁刚度比变化)的敏感区域,可为设计人员在满足实际功能需求的前提下,确定合理的柱梁刚度比,进而改善结构受力节省工程造价提供参考。值得注意的是,地铁车站功能需求及标准轨节长度决定轨排井洞口长度与车站侧墙高度比值大于2,扶壁柱柱底控制弯矩解析解的理论推导及假定是建立在这一前提条件下,不能被忽视。
