洄河石拱古桥运营期结构安全仿真分析

杨振威， 任克彬， 谭亚可

(1.河南省文物建筑保护研究院， 河南 郑州 450002；2.河南星联置地集团有限公司， 河南 郑州 450008)

石拱古桥建成年代久远，受战火洗礼、环境侵蚀等因素的影响，石拱古桥部分遭到破坏，但由于部分石拱桥身处交通要道，因此仍然承担着交通运输的重任。相对于现代桥梁来说，石拱古桥建造时缺少相应规范校核，且受当前交通流量增大、频繁承载甚至超载等交通环境恶化的影响，加上石拱桥结构与材料性能的退化，仍在通行利用的石拱古桥安全性往往存在较大的安全隐患。古代桥梁不仅对研究我国古建筑技术的发展具有极其重要的意义，而且对于认知古代社会的历史、文化、艺术以及政治、外交、经济等具有无法替代的价值。如何确保古桥尽可能完整的保存下去，保持其良好的运营状态，延长其使用寿命至关重要[1-2]。

对于古桥遗存的保护来说，由于其不可再生性，为保障古桥安全，需要对它进行科学的监测、评估与修缮。由于结构体系的物理参数、边界条件与结构的病害状况有关，为了更精准的了解结构的状况，需要进行仿真分析[3-6]，以达到预测和控制结构内力和变形的发展及变化，从而保证结构在安全范围内工作。

对古桥内力和变形的计算是其综合性能评定的重要一环，国内学者采用有限元分析的方法对此开展了广泛的研究工作。李正英等[7]将拱桥简化为平面杆系模型，进行动态仿真分析，并考虑了行波效应对减震效果的影响。何伟等[8]按设计施工顺序进行了面向施工全过程仿真分析，研究了施工过程中的结构应力及其增量等变化规律。李小珍等[9]提出了一种采用几何非线性有限元法，对大跨度悬索桥施工状态进行计算机仿真分析。郑凯锋等[10]认为全桥空间结构模型、模型边界真实性和模型加载真实性等特征在全桥结构仿真分析中的综合应用，将提高分析结果的准确性和实用性。周岑等[11]全桥结构仿真分析技术在大跨度石拱桥的分析计算中，能得到较传统计算理论更加详尽和精确的结果，有着良好的应用前景。石明兰等[12]指出石拱桥加固前后的有限元分析计算结果与实测动力特性结果相符，其有限元模型适用于动静力特性计算。胡崇武等[13]找到了分步施工石拱桥施工仿真控制及分析方法，发现了拱脚高应力区。

魏召兰等[14]对实腹式石拱桥合理计算模式研究，从拱轴线变化和拱圈边缘应力的角度进行评价得到有益的结论。聂建国等[15]对700年石拱桥的分析结果表明，石拱桥具有明显的空间协同工作能力，根据理论分析和试验所确定的材料力学参数可用于预测类似结构的工作性能。

为此，文章根据漯河市郾城区裴城镇裴城村小洄河上的洄河石拱桥的结构特点[16]，结合相关规范[17]要求，基于有限元分析软件ANSYS建立洄河石拱桥整体模型，计算了多种工况下拱桥挠度和应力的变化规律，所得结论可为古石拱桥的研究提供参考。

1 验算标准

拱桥结构分析是基于结构有限元基准模型开展的。修正有限元基准模型参数使其计算结果与实际结构尽可能相符是保证其最终结果准确性的先决条件。目前主要根据拱桥实测结果采用优化方法对结构质量和刚度矩阵进行修正或者对设计参数进行修正。本文以拱桥振动频率、跨中挠度为响应量，反演建立拱桥高精度有限元模型。

根据等效刚度法，拱桥的弹性模量作如下折算：

EA=EaAa+EfAf

(1)

式中：Aa、Ea为横截面拱圈中块石面积、弹性模量；Af、Ef为横截面拱圈中胶结材料面积、弹性模量。

拱圈质量为:

M=Ma+Mf

(2)

式中:Ma为拱圈中块石质量；Mf为胶结材料质量。

短期效应组合作用下，在一个桥跨范围内的正负挠度的绝对值之和的最大值不应大于计算跨径的L/1000[16-17]。洄河石拱桥正常使用极限状态竖向挠度满足

(3)

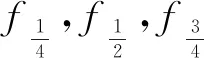
当石料的抗压强度设计值和砌体的抗压强度设计值不同时，验算和设计过程中应以砌体抗压强度设计值为准[14]。为偏于安全，按照旧规范《公路砖石及混凝土桥涵设计规范》[18](JTJ 022—85)洄河石拱桥部分料石、砂浆最低设计标号强度要求如表1所示。

表1 砌体强度

2 工程概况

洄河石拱桥位于河南省漯河市郾城区裴城镇裴城村，根据其所用石料及建筑技法可以判定该桥为北宋年间建造。该桥由红色砂页岩砌筑而成，桥东西长8.30 m、南北宽6.47 m，桥拱净跨2.92 m、矢高1.98 m。桥拱由18道拱石并列砌筑而成，券面石边除两道凸弦纹外其余均为素面拱券与券基石，中间由生铁和黏合剂填充，拱券两侧桥基以石磙做基础加固。桥上原有青石栏杆，栏板上刻有各种动物图案。

有关洄河石拱桥设计和建造的文字记载极其匮乏。经现场踏勘和测量完成该桥的图纸绘制，如图1所示，详细记录了古桥的技术资料和运营现状。随着交通流量和桥梁负荷的日趋增大，以及自然因素和人为因素的综合影响，受力结构(拱圈)已经产生了一定程度的损伤，病害特征明显增大，安全隐患突出。

图1 洄河石拱桥示意图

3 石拱桥数值模型

洄河石拱桥有限元模型通过ANSYS建立，如图2所示。拱桥结构采用Solid 65单元模拟，共37 700个单元，43 472个节点。将拱桥模型单元材料属性依实际情况分为2组，第一组为拱圈单元，第二组为拱上结构单元。采用直角坐标系，上游拱脚中点设置为坐标原点，顺桥向为X轴，竖直向上为Y轴，横桥向为Z轴。模型底部约束X、Y、Z轴向线位移，桥梁两端横断面采用法向链杆约束。为便于计算结果说明，在拱圈的有限元模型中，沿控制截面(纵向)节点设置两条路径，其中顺桥向左拱脚为拱圈控制截面零点位置，净长2.92 m。拱圈控制截面节点路径如图3所示。

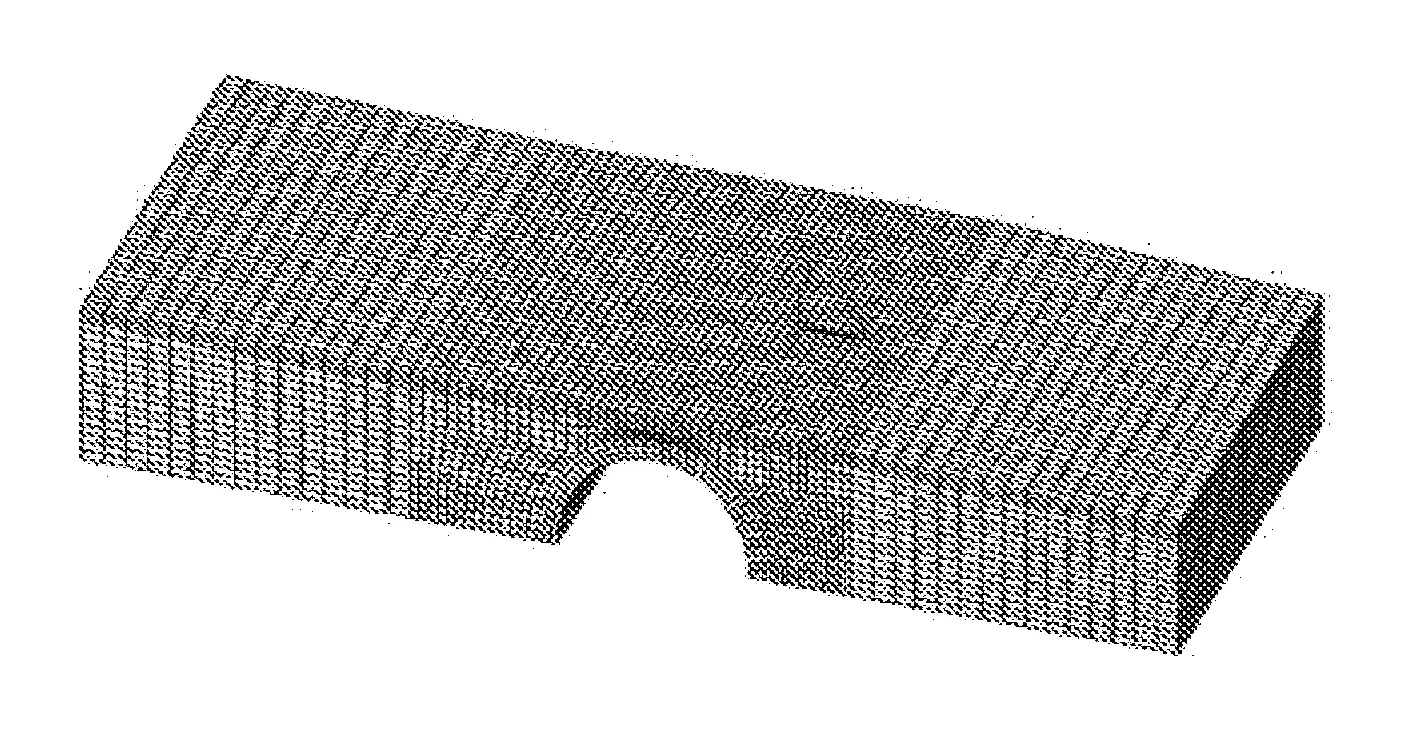
图2 有限元模型图

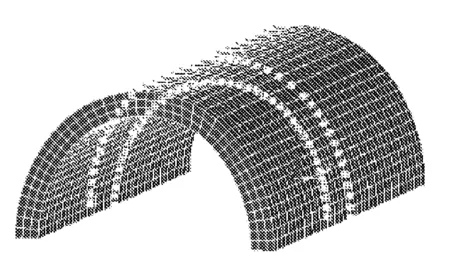
图3 节点路径

为了增加数值分析的准确性和适用性，根据现场测试石拱桥固有频率等动力特性结果采用响应面方法修改拱桥初始模型得到拱桥基准模型。动力测试传感器选用国家地震局工程力学研究所的891型测振仪，将其固定在拱圈拱脚、l/4、l/3及跨中位置处，数据采集处理DH5907桥梁模态振动测试系统。经修正后有限元模型中石材标号MU30。根据式(1)与式(2)计算得到模型材料弹性模量与密度。拱上结构密度2 000 kg/m3，弹性模量0.285 GPa，泊松比为0.3；主拱圈密度2 400 kg/m3，弹性模量5.65 GPa，泊松比为0.25。基准模型计算拱桥振动频率如表2所示，可以看出其计算值与实测值最大误差不超过2.25%，因此基准模型反应了拱桥结构特性。

表2 拱桥固有频率有限元值与实测值比较

石桥在运营期内，共计算以下6种工况：

(1) 工况1：单车道加载，汽车后轮在拱桥1/4跨。

(2) 工况2：单车道加载，汽车后轮在拱桥1/2跨。

(3) 工况3：单车道加载，汽车后轮在拱桥3/4跨。

(4) 工况4：双车道加载，汽车后轮在拱桥3/4跨。

(5) 工况5：双车道加载，汽车后轮在拱桥1/2跨。

(6) 工况6：双车道加载，汽车后轮在拱桥1/4跨。

4 运营期安全性分析

各工况下沿路径各节点挠度如图4所示，各工况下沿路径各节点X方向应力、Y方向应力、Z方向应力如图5—图10所示，各工况下路径上各节点第一主应力、第三主应力计算结果如图11—图14所示。

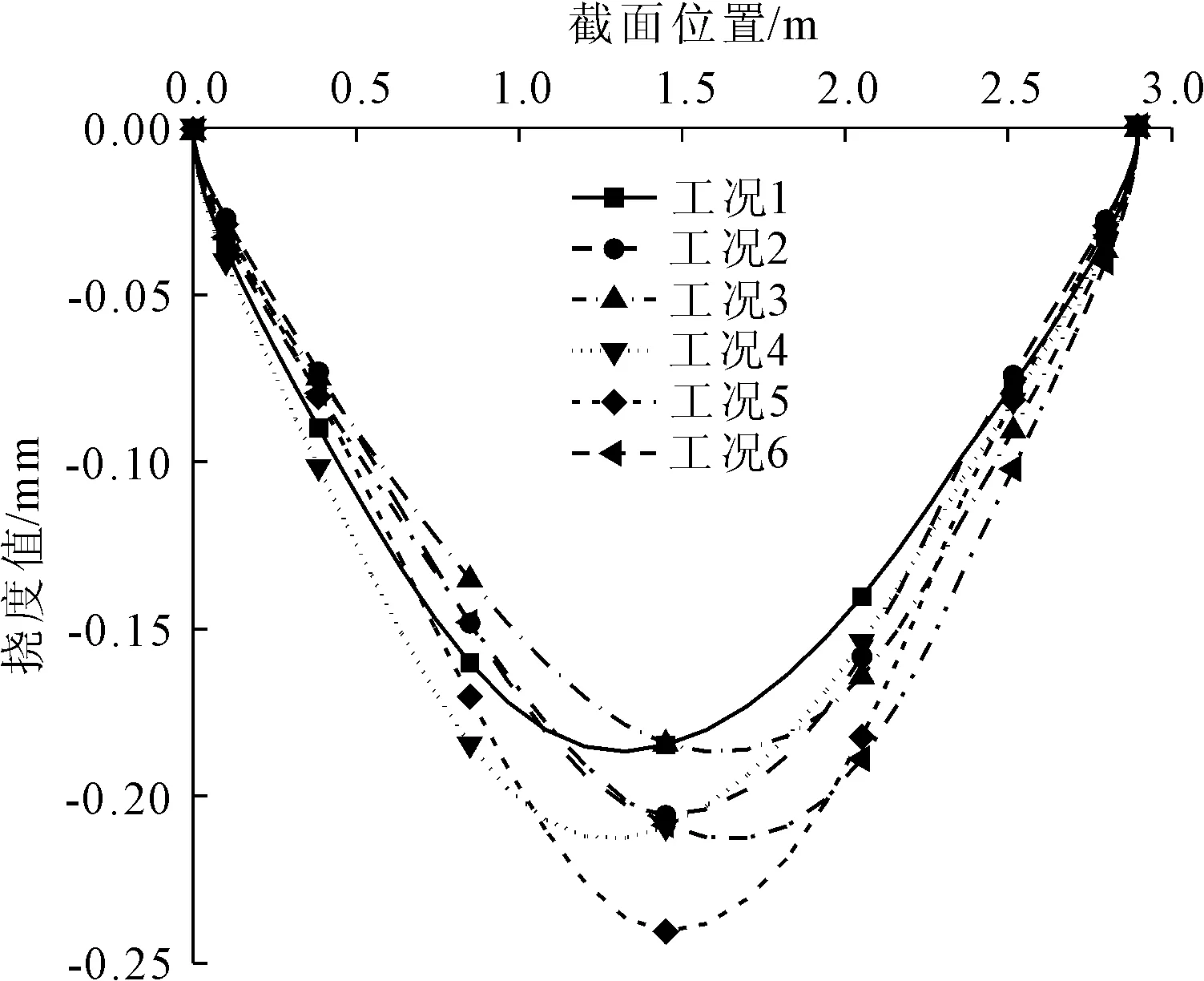
图4 顺桥向控制截面挠度

从图中不难发现工况5为运营期受各种荷载影响最不利工况，因此以工况5为例，重点分析洄河石拱桥拱圈在运营期的常见荷载作用下拱圈挠度与应力分布情况：

(1) 挠度特征。由图4可以看出，拱圈挠度的最大值分布在跨中，从两侧拱脚向跨中逐渐增大并呈对称分布。按照规范规定的作用短期效应组合，在一个桥跨范围内正负挠度的绝对值之和的最大值为0.550 mm，小于规范允许值2.92 mm。六种工况下最大挠度均位于跨中附近，随着拱圈受荷载的增大而增加。各工况下控制截面最大挠度为工况2作用下的0.206 mm，计算可得一个桥跨范围内的正负挠度绝对值之和的最大值为0.477 mm，控制截面最大挠度为工况5作用下的0.241 mm，此时一个桥跨范围内正负挠度绝对值之和最大值为0.550 mm，均小于规范允许值，且有限元分析中挠度分布规律符合无铰简支拱桥的受力特点。

(2) 应力特征。由图5和图6可以看出，工况5时，拱圈的X向应力值压应力最大值为0.243 MPa，拉应力最大值为0.339 MPa。拱圈X向的应力最值分布在跨中，压应力值从两侧拱脚向跨中先增大再减小并呈对称分布，拉应力值从两侧拱脚向跨中先减小再增大，同样呈对称分布。

图5 各控制截面X方向压应力极值图

图6 控制截面X方向拉应力极值

由图7和图8可以看出，工况5时，拱圈Y向控制截面拉、压应力值变化图均呈对称分布，且两图应力变化规律相似。拱圈的Y向最大压应力为0.402 MPa，位于拱脚处。拱圈的Y向最大拉应力为0.009 6 MPa，大约位于净跨1/3处。

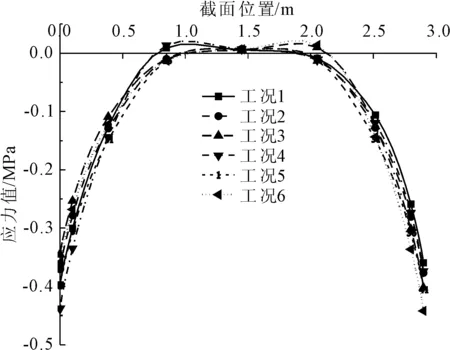
图7 顺桥向控制截面Y方向受压应力

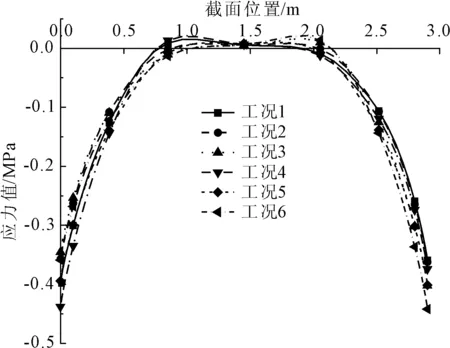
图8 顺桥向控制截面Y方向受拉应力

由图9和图10可以看出，工况5时，拱圈Z向压应力控制截面最大值为0.081 2 MPa，位于跨中位置，应力值从两侧拱脚位置至跨中，先由拉应力逐渐减小为零，然后压应力逐渐增值最大，呈对称分布。拱圈Z向拉应力控制截面最大值为0.127 MPa，位于跨中位置，应力值从两侧拱脚位置至跨中，先由压应力逐渐减小为零，然后拉应力逐渐增值最大，同样呈对称分布。

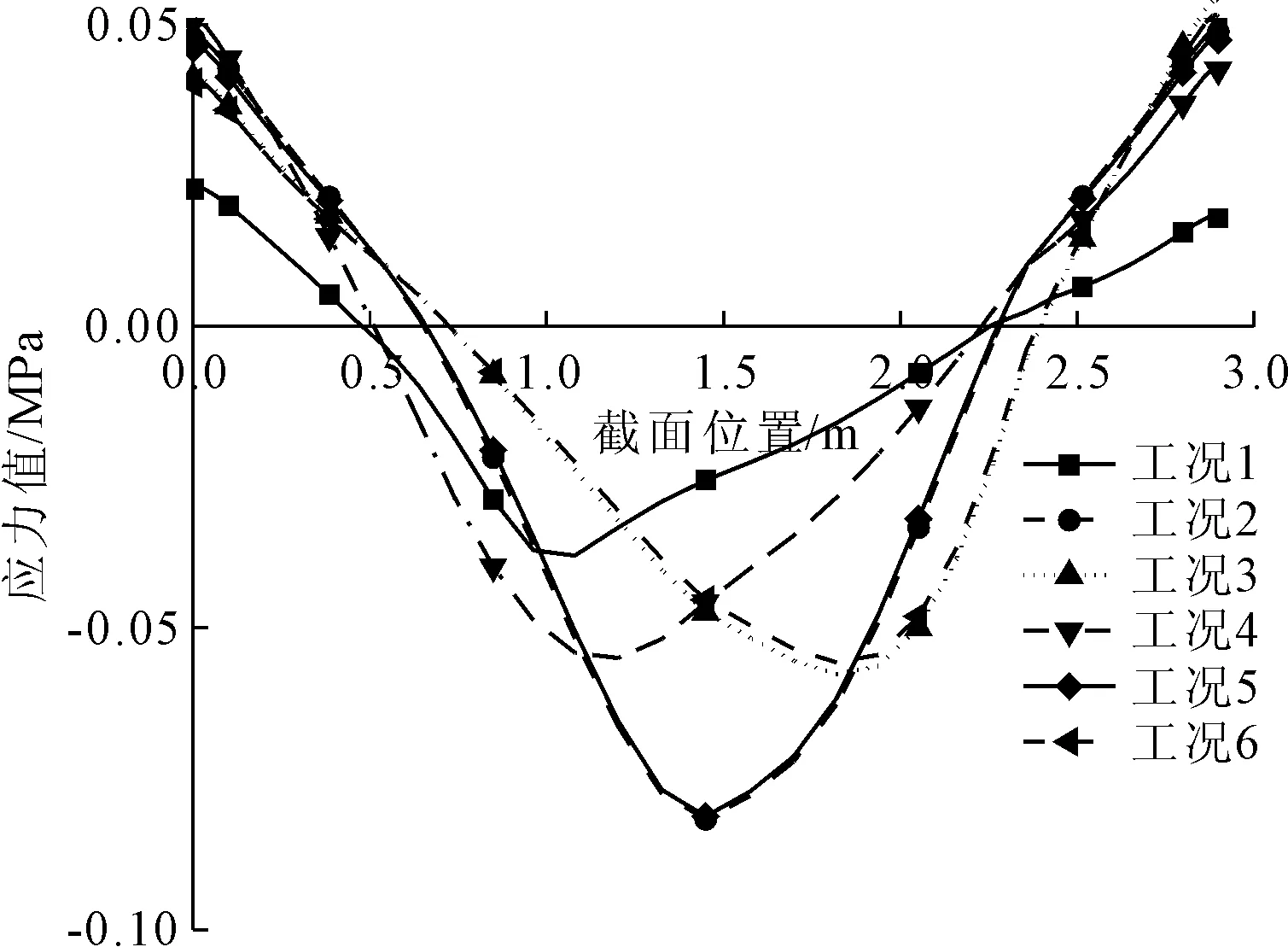
图9 顺桥向控制截面Z方向受压应力

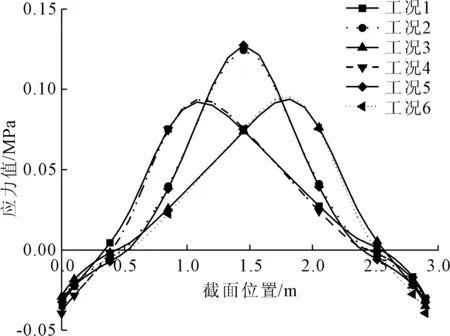
图10 顺桥向控制截面Z方向受拉应力

由图11和图12可以看出，工况5时，拱圈第一主应力受压控制截面最大压应力位于跨中位置，应力值从两侧拱脚位置至跨中，呈对称分布。拱圈第一主应力收拉控制截面最大拉应力位于跨中位置，应力值从两侧拱脚位置至跨中，逐渐增大，呈对称分布。

图11 顺桥向第一主应力控制截面压应力

图12 顺桥向第一主应力控制截面拉应力

由图13和图14可以看出，工况5时，拱圈第三主应力控制截面拉、压应力值变化规律相似，均呈对称分布，且跨中 0.5 m范围内应力值图像平缓，近似于静力平衡状态，表明结构在此应力状态下安全、稳定。拱圈第三主应力最大压应力为0.407 MPa，位于拱脚处，最大拉应力为0.009 8 MPa，大约位于跨中附近。第三主应力控制截面，除跨中0.5 m范围内应力接近平衡状态外，余下部分全部受压，且两侧拱脚处压应力达到最大。

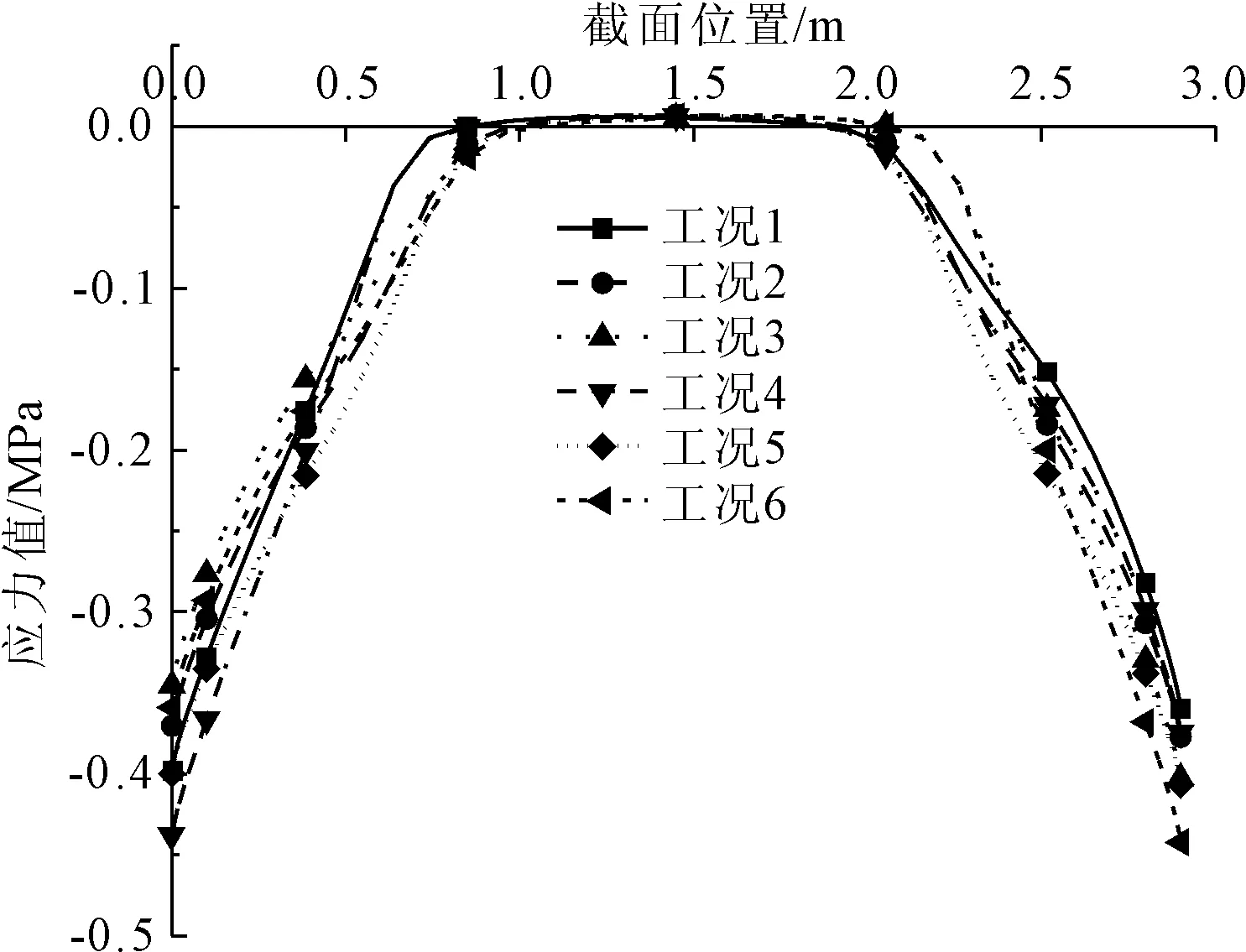
图13 顺桥向第三主应力控制截面压应力

图14 顺桥向第三主应力控制截面受拉应力

综上，工况5时，顺桥向拱圈控制截面压应力最大值为第三主应力0.402 MPa，顺桥向拱圈控制截面拉应力最大值为X向应力和第一主应力0.339 MPa，小于表1规范中块石砌体拉、压强度值0.66 MPa、4.30 MPa，表明在最不利工况5时，拱圈的挠度、应力均满足《公路砖石及混凝土桥涵设计规范》[18](JTJ 022—85)相关规定，结构安全。

从图5、图6及图9—图12可以看出运营期拱圈X、Z向应力和第一主应力控制截面均在工况5作用下，不同工况下随着拱圈受荷载的增大而增加；从图8和图9可以看出，拱圈Y向控制截面应力在工况4作用下，拱圈Y向控制截面应力在工况6作用下，运营期拱圈的Y向最大压应力为0.442 MPa，位于拱脚处。运营期拱圈的Y向最大拉应力为0.020 2 MPa，大约位于净跨1/3处。此方向各工况控制截面拉、压应力值变化图从跨中至两拱脚压应力逐渐增大且呈对称分布，比较Y向拉、压控制截面应力图发现二者应力变化规律相似。

从图13和图14可以看出，运营期拱圈控制截面第三主应力最大值为在工况6作用下0.443 MPa，位于拱脚处。六种工况下跨中 0.5 m范围内应力值图像平缓。此方向各工况控制截面拉、压应力值变化图从跨中至两拱脚压应力逐渐增大且呈对称分布，比较第三主应力拉、压控制截面应力图发现二者应力变化规律相似。

综上，拱圈控制截面挠度、应力整体呈对称分布，各工况作用下分布规律满足无铰拱的受力特点。拱桥拱圈的挠度、应力满足《公路砖石及混凝土桥涵设计规范》[18](JTJ 022—85)规范相关规定，因此可以认为洄河石拱桥运营期结构安全。

(3) 工况5计算结果。限于篇幅，下面给出工况5时拱圈挠度、X方向应力、Y方向应力、Z方向应力、第一主应力、第三主应力的ANSYS计算结果云图，如图15—图20所示。分析其简要特征如下：

由图15可以看出拱圈全跨范围内下挠，且跨中附近下挠较大，从跨中向两拱脚挠度变小，单处最大挠度为0.24 mm。

图15 挠度计算云图

由图16可以看出拱圈X方向的最大压应力为0.244 MPa，位于拱圈上表面跨中附近；最大拉应力为0.343 MPa，位于拱圈下表面跨中附近。由图17可以看出拱圈Y方向的最大压应力为0.406 MPa，位于拱圈上表面跨中附近；最大拉应力为0.016 MPa，位于拱圈下表面跨中附近。由图18可以看出拱圈Z方向的最大压应力为0.082 MPa，位于拱圈上表面跨中附近；最大拉应力为0.129 MPa，位于拱圈下表面跨中附近。

图16 X向应力计算云图

图17 Y向应力计算云图

图18 Z向应力计算云图

由图19可以看出拱圈第一主应力的最大压应力为0.066 MPa，位于拱圈上表面跨中附近，最大拉应力为0.343 MPa，位于拱圈下表面跨中附近。对于其拱圈上表面跨中附近出现的应力集中，考虑到数值分析时，荷载是以集中力的方式加载，而实际结构中由于拱上结构的扩散作用，拱圈不易出现应力集中，因此图中应力集中区可予以忽略。由图20可以看出拱圈第三主应力的最大压应力为0.407 MPa，位于拱圈下表面拱脚附近，最大拉应力为0.013 MPa，位于拱圈下表面跨中附近。

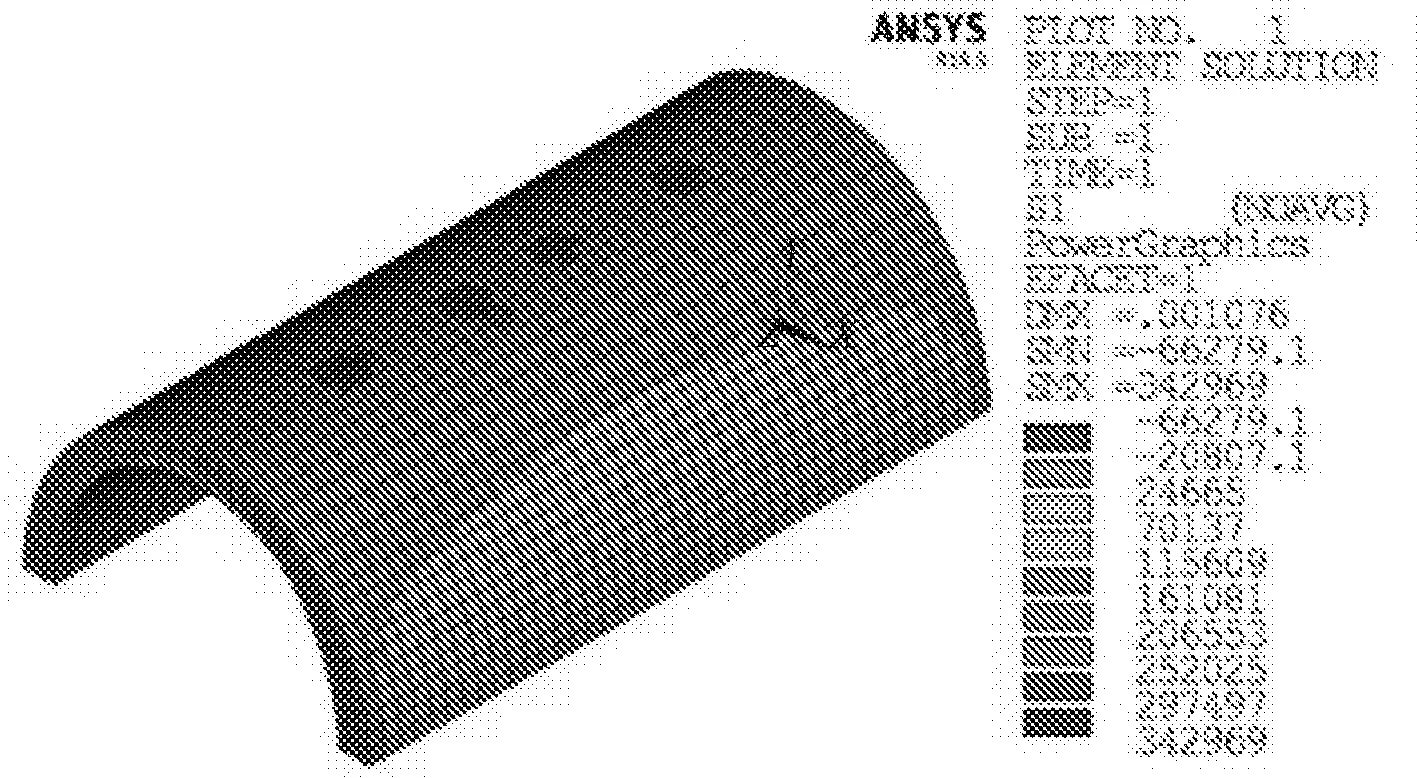
图19 第一主应力计算云图

图20 第三主应力计算云图

综上所述，可以看出拱圈的挠度及应力均小于规范允许值，故结构安全。

5 结 论

(1) 洄河石拱桥在运营期受重力、车载等作用时，拱圈的挠度与应力分布规律符合石拱桥的受力特点，应力、挠度呈现明显的对称性。

(2) 挠度、应力随着拱圈承受荷载的增加而增大，各工况下，有限元计算结果均满足规范要求，因此古桥现行运营状况下结构安全。