等离子去板坯熔渣机器人运动学分析与研究

李 龙，朱宝林，陈 双

（芜湖哈特机器人产业技术研究院有限公司，安徽芜湖 241000）

0 引言

我国是钢铁行业的制造和使用大国，目前主要采用的是数控火焰切割机处理大型的机械加工件，因摸具制造和铸造工艺等原因，在火焰切割后，造成熔融的钢液向下流动，从而会使板坯底部出现毛刺甚至飞边，造成装配精度的降低，甚至影响轧钢的表面质量。现阶段，使用较多的去毛刺机主要是刮刀式、锤刀式[1-3]。研究结果表明，两种方法具有一定的局限性，去除毛刺效率不高，质量一般，且轧钢的生产效率受刀具寿命及质量的影响[4-5]。

本文提出了一种利用等离子切割机器人去除板坯熔渣的方法，设计了专用的去板坯熔渣机器人，并对该机器人进行运动学建模及分析研究，经前期试验，该方法不仅速度快而且切割质量非常好，能达到工业实时生产要求。

1 等离子切割机器人运动学模型的建立

对于机器人各个连轴之间的关系，Denavit 和Hartenberg[6]提出了将运动学关系精简为齐次变换矩阵的数学运算问题，本文的运动学采用目前国内科技文献常用的Craig[7]版本（也称为前置法），设计了专用的五自由度机械手三维模型，如图1所示，由底座、腰、大臂、小臂和腕关节5个转动关节组成，建立各关节处的坐标系（坐标系0～5），其中坐标系0 与坐标系1重合。

图2 所示为机械轴的机构简图，图中标注了各关节相应尺寸及坐标系相对位置。杆件参数及相关变量如表1所示，其中θi是绕zi轴，从xi-1旋转到xi的角度；αi-1是绕xi轴，从zi旋转到zi+1的角度；ai-1是沿xi轴，从zi移动到zi+1的距离；di是沿zi轴，从xi-1移动到xi的距离。

图1 三维模型

图2 机构简图

表1 杆件参数和关节变量表

2 运动学分析

2.1 正运动学

机器人的正运动学问题为：已知机器人的结构参数及各关节变量，在参考坐标系中，获取其末端执行器的位姿。每个关节i两侧的连杆i对连杆i-1的相对位置可由一个4×4的矩阵来表示[8]：

式（1）由参数ai-1、αi-1、di、θi决定，只有θi为变量，即变换矩阵随θi变化而变化。文中连杆坐标系O5-X5Y5Z5相对于基坐标系O0-X0Y0Z0变换矩阵为各变换矩阵相乘。由式（1）和表1可得：

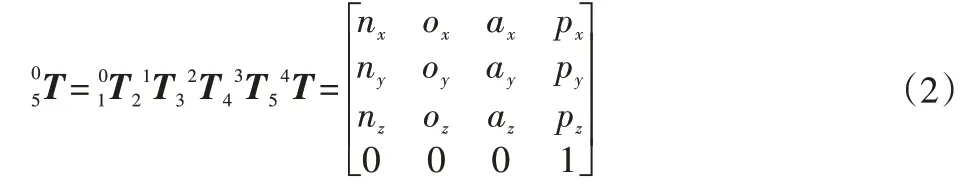
由图2可知，各关节角度为：θi＝[0° 0° 6.38° 83.62° 0°]，并代入式（2），得出机器人末端相对于参考坐标系的位置和姿态，结果为：

2.2 逆运动学分析

目前工业机器人求解逆运动学的一般方法为反变换法[9-10]（也称代数方法），该方法求解多次逆乘，计算较繁杂。本文将提出一种改进求解算法，只需逆乘一次，即可将所有的关节变量求出来，过程如下。

将式（2）变形为：

（1）求解θ1

令式（4）两端的元素（3,4）相等，可得：

（2）求解θ2

令式（4）两端的元素 (1,4) 、 (2,4) 、 (1,3) 、 (2,3)分别对应相等即得4个方程：

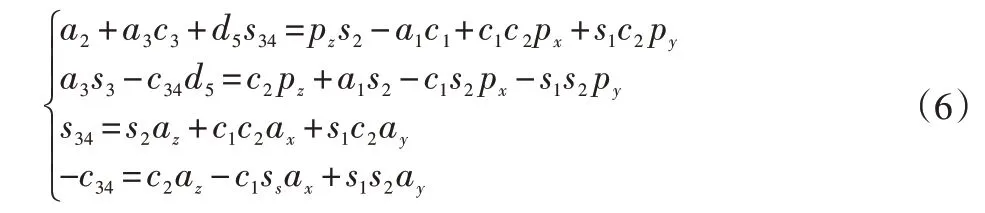
整理得：

解得：

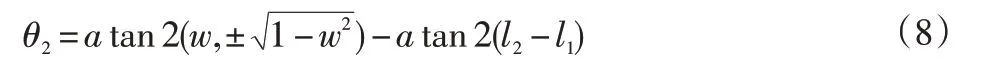
（3）求解θ3

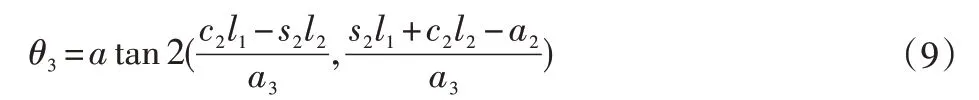
（4）求解θ4

（5）求解θ5

综上，可得一组关节角度的解为：q ＝ [0°, 0°, 6.38°,83.62°,0°]。

2.3 逆解中多解问题的处理

从上文解的表达式中可知θ1和θ2有2 个根，故存在4 组解，而控制机器人运行需要唯一确切的解。本文提出了一种从逆解中的多组解中寻求控制机器人的最优解的方法：采用双变量反正切函数确定关节角后，在不考虑避障的情况下，以机器人移动最短具体为前提后获取各关节θ的最优解，将所得的最优解作为实现机器人目标位姿的控制依据[11-14]

3 验证

在MATLAB 环境下利用Robotics Toolbox 工具箱对运动学模型进行分析验证，流程图如图3所示。

3.1 机器人运动模型的建立

机器人模型建立步骤如下：

（1）调用Link()函数，并输入表1 中的连杆参数。Link()函数的调用格式为：

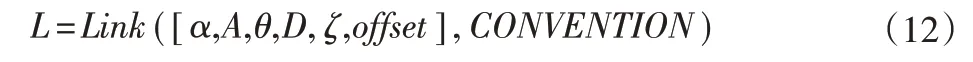
式中：α为连杆扭转角αi；A为连杆长度ai；θ为两连杆夹角；D为2 个连杆间的距离；ζ为关节类型；offset为关节的偏移量；CONVENTION可以取standard 或modified，本文取modified，即采用改进的D-H参数。

（2）调用SerialLink() 函数，SerialLink() 函数的调用格式为：

式中：L1,L2,⋅⋅⋅,Ln分别机器人的各个连杆。

（3）调用drivebot()函数，生成三维模型及控制界面。

图3 运动学验证流程图

综上所述，Matlab中机器人D-H参数表如图4所示，生成三维模型如图5所示。

3.2 运动学仿真验证

3.2.1 正运动学仿真验证

调用fkine()函数，得出正运动学末端位姿矩阵。

式中：robot为机器人模型；q为机器人的一组关节角度值。

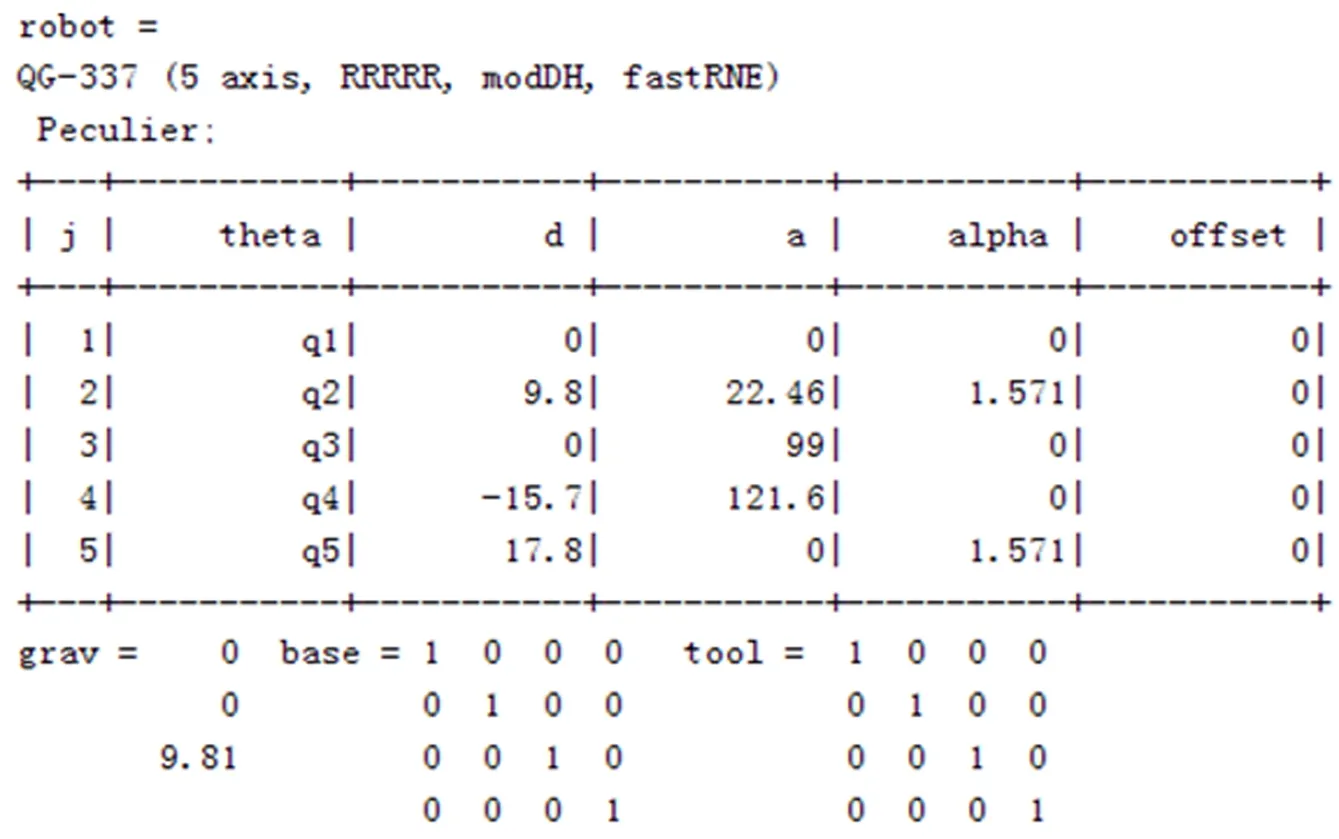
图4 Matlab中机器人D-H参数表

图5 Matlab中机器人三维模型

将机器人初始位置q0＝[0 0 6.38×π/180 83.62×π/2 0]代入，可得图6所示的结果。将其与第二节所计算的正运动学结果相比较，可以得出两者结果一致。

图6 在MATLAB中的正运动学结果

3.2.2 逆运动学仿真验证

调用ikine()函数，求解逆运动学方程

式中：T 为机器人末端的姿态；q为机器人初始关节角度；M 为一个1×6的矩阵；其中的每一个元素代表机器人的一个关节自由度。故本文机器人的M 矩阵为[1 1 1 1 0 1]。求解结果如图7所示。将图中所得结果qi＝[0,0,0.111 4,1.459 4,0]转化为角度值为qi＝[0°,0°,6.39°,83.61°,0°]，经与理论计算的部分相比较，两者结果一致，所得的解完全符合所赋初值。

图7 逆运动学求解的结果

4 结束语

（1）本文提出了用等离子切割机器人去除板坯熔渣的新方法，并自行设计专用的五自由度机器人。该方法可以高效快速地去除板坯熔渣，也增加了机器人在冶金领域的新应用。

（2）得到了五自由度机器人的正运动学解及逆运动学解。在求解逆解的过程中提出了一种改进的算法，仅用一次矩阵的逆乘便求出所需的解，避免了大量矩阵逆乘，使运算过程更加简单。

（3）使用MATALB 中的Robotics 工具箱验证了所求运动学的结果。经两者比较结果说明，在忽略计算误差的基础上，两者保持一致，从而验证了所建立模型的正确性及相关理论计算的正确性。