抛物线-圆弧型封头的设计优化
2020-08-26刘星凌一玮苏文献李业勤
刘星,凌一玮,苏文献,李业勤
(1. 上海理工大学能源与动力工程学院, 上海 200093; 2. 中国船舶重工集团公司第七一一研究所, 上海 201108; 3. 常州化工机械厂,江苏 常州 213002)
封头的形状对其应力状态和临界载荷有着重要的影响。近年来,研究人员已经对椭圆形封头、碟形封头等标准凸形封头与圆筒体连接的边缘应力进行了大量研究。Md.Wahhaj Uddin[1]分析了椭圆形封头与圆柱形筒体连接区域,比较了线性壳理论得到的应力分布与实际情况。Guodong,C.[2-3]分别给出了压力容器中碟形封头和椭圆形封头的复杂方程以及渐近解。Bushnell,D[4]利用计算机程序,计算了椭圆形封头和球形封头与筒体组合壳体的应力状态。K. Magnucki 等[5-6]研究内压作用下圆柱形压力容器中椭圆形封头的应力问题。高炳军等[7]研究了碟形封头的结构特征,计算了影响其强度情况的参数,利用ANSYS 软件模拟计算出不同尺寸结构的碟形封头应力状态。张迪[8]对碟形封头的两个参数进行优化设计,得到了一种新型碟形封头,减小了封头边缘应力。至目前为止,虽然国内外研究人员对于封头的相关研究已经做了不少工作,但是针对的大都是现有的标准封头。碟形封头与筒体相接处以及过渡段小圆弧和中间大圆弧之间曲率的突变产生较大的二次应力及局部薄膜应力,对于承压性能产生巨大影响。针对碟形封头力学性能方面的不足,本文设计并优化出一种应力状态更好的抛物线-圆弧型封头,能够提高封头的承压性能,降低制造难度,节约生产成本,实现高效率的生产。
1 抛物线-圆弧型封头的设计
1.1 抛物线-圆弧型封头的设计思想
碟形封头存在的不足是筒体与封头过渡段、封头过渡段与球面的连接区域,应力与变形不连续,存在明显的边缘应力。考虑到碟形封头与筒体相接处以及过渡段小圆弧和中间大圆弧之间曲率的突变产生较大的二次应力及局部薄膜应力,设计使用一段抛物线来代替碟形封头中间的过渡段圆弧,减少不同形状的壳体相连产生的曲率突变,进一步减少突变造成的边缘应力,如图1 所示。
1.2 满足结构连续性条件的抛物线方程
带有抛物线-圆弧型封头的圆筒形压力容器由球壳、抛物线组成的特殊旋转壳体和直边圆筒体组成。抛物线-圆弧型封头的经线由圆弧和抛物线组合而成。封头由部分球壳(图2 中的MO")和抛物线生成的部分特殊旋转壳体(图2 中的MO)组成。
一般的抛物线方程可以表示为:


图1 抛物线-圆弧型封头的示意图Fig.1 Schematic diagram of the parabolic-arc head

图2 抛物线-圆弧型封头的经线Fig.2 Warp of the parabolic-arc head
由抛物线旋转而成的壳体的第一曲率半径:

第二曲率半径:
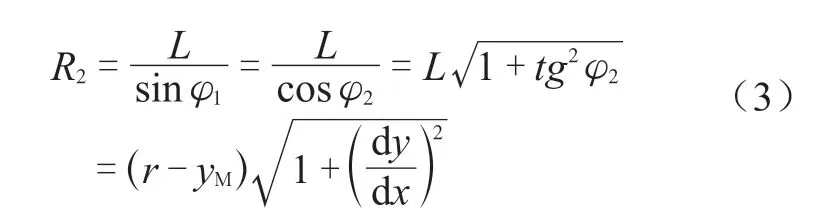
这里,取筒体和封头的厚度相同,材料相同,结构的连续性条件如下:
(1)在直边段筒体与抛物线旋转壳体连接处
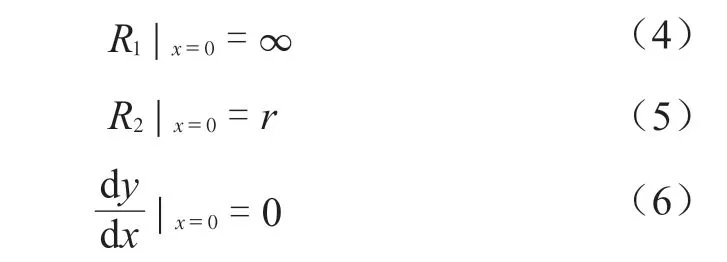
(2)在球壳与抛物线旋转壳体连接处

把式(1)代入式(3)后,由(5)得:

把式(1)代入式(6)后得:

因此满足结构连续性条件的抛物线方程为:

1.3 抛物线-圆弧型封头中面的设计方法
在图3 的坐标系xoy 中,作抛物线方程的曲线:


图3 抛物线-圆弧型封头的中面经线Fig.3 The mid-surface warp of the parabolic-arc head
为了方便计算,假设:


当2 ≤b ≤3 时,所作曲线在原点处二阶导数为零,这样所形成的封头在原点处不会产生第一曲率半径的突变,仍和筒体一样为∞,从而减缓实际边缘应力。因为抛物线两个参数a、b 以及封头不带直边深度与半径的比值m 是相互制约的,当这两个值确定,另一个值m 必然确定。为了方便与标准封头比较,也考虑到m 取0.5 时,从制造的角度看比较合适,于是取m 的值为0.5。
因此,组成抛物线-圆弧型封头特殊旋转壳体的抛物线方程变为:

2 抛物线-圆弧型封头的静力分析
通过分析和试算,式(19)中的a、b 分别取为0.887 8 和2,也就是抛物线方程为y = f ( x ) = 0.887 8 x2。根据广义轴对称理论,选取筒体和封头的四分之一轴对称平面模型进行建模分析,在保证模拟结果准确性的前提下,简化了有限元模型,为后面的网格处理和计算过程节省时间。封头的结构参数见表1,性能参数见表2。

表1 抛物线-圆弧型封头结构参数Table 1 Structure parameters of the parabolic-arc head

表2 抛物线-圆弧型封头性能参数Table 2 Performance parameters of the parabolic-arc head
2.1 几何模型及网格划分
对于承受均匀内压的压力容器筒体与封头,使用轴对称二维模型计算的结果与三维实体模型对比后很相近,但是二维模型进行计算需要的时间少得多,因此对所要研究的抛物线-圆弧型封头结构建立轴对称二维模型。为了更好地了解边缘应力的影响情况,筒体长度应该远远大于边缘效应的范围。使用ANSYS 软件建立的模型见图4。
使用8 节点183 实体单元轴对称平面单元,网格沿着厚度方向分为三层,总共划分300 个单元。考虑到整个模型几何形状的对称性,在Element behavior 选项中选择Axisymmetric,将其设置为轴对称模型。抛物线-圆弧型封头的网格划分图如图5所 示。

图4 抛物线-圆弧型封头几何模型Fig.4 Geometry model of the parabolic-arc head

图5 抛物线-圆弧型封头网格划分Fig.5 Meshing diagram of the parabolic-arc head
2.2 边界条件
筒体的底部不能发生轴向位移,所以对其施加轴向约束,限制Y 方向上的位移。对称面不能发生水平位移,所以对其施加对称水平约束,限制X 方向上的位移。模型内壁面承受均匀内压,均匀内压施加到模型的内表面,完成加载约束后对有限元模型进行求解。抛物线-圆弧型封头的边界设置如图6 所示。

图6 抛物线-圆弧型封头边界条件图Fig.6 Boundary condition diagram of the parabolic-arc head
2.3 数值计算结果
均布内压4 MPa 下抛物线-圆弧型封头的等效应力分布见图7。

图7 抛物线-圆弧型封头等效应力云图Fig.7 Equivalent stress cloud map of the parabolic-arc head
3 抛物线-圆弧型封头的结构优化
3.1 优化设计概述
传统的设计方法是凭借自身的经验进行初步设计,再利用理论知识对初步方案进行计算分析。如果该方案不符合设计需求,重新修改设计参数,进行重复计算设计。整个过程不仅耗时长,而且最后的设计结果大部分并不是最优的设计。优化设计是一种高效的设计方法,当处理复杂任务的时候,可以在各种方法中求解出最合适的结果[9]。
3.2 优化变量
不同抛物线所组成壳体的形状不同,导致了抛物线-圆弧型封头中应力状态的差异。决定抛物线形状的参数a 和b,可以用封头的深度比m 来关联。如果确定一个b 和m 的值,也就能确定一个唯一的a 值。考虑到m 取0.5 时从制造的角度看也比较合适,于是就取m 为0.5。综上所述,优化变量是组成抛物线旋转壳体的抛物线方程系数b。
3.3 约束条件
本次优化分析主要优化变量抛物线方程系数b的约束范围是2 ~ 3。

表3 优化变量取值范围Table 3 The value range of the optimized variable
优化变量的取值是离散的,0.01 的变化幅度对于应力强度最大值的改变为0.38%,综合考虑计算时间和精度,将优化变量的变化幅度定为0.01。
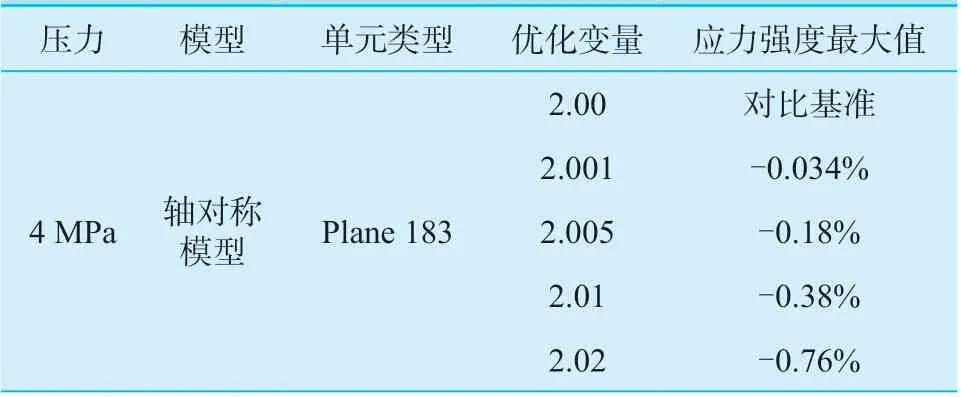
表4 模型计算结果对比Table 4 Comparison of calculation results of the model
3.4 优化过程
(1)确定特征参数和设计参数的初始值。σmax为抛物线-圆弧型封头的最大应力强度值。因为曲率中心的坐标α、β 以及曲率半径R 都受到抛物线表达式中参数b 的影响,也就可以把这三个参数的优化转换为对抛物线方程参数b 的优化。
(2)设定特征参数和设计参数的变量范围。
(3)确定目标函数,寻找应力强度最小的抛物线-圆弧型封头结构。
(4)使用Pro/E 建模软件建立模型,经过初步设计后,建立抛物线-圆弧型封头的二维几何模型。根据抛物线-圆弧型封头的结构参数和尺寸,建立抛物线-圆弧型封头的二维几何模型,生成可以后续被调用的输入数据文件。
(5)ANSYS 负责静态分析,调用Pro/E 的输入文件,进行有限元应力分析,通过数值模拟计算出模型的应力应变分布情况。将参数化的模型文件导入到ANSYS 有限元分析软件,画好网格后设置约束和载荷,进行结构优化分析;使用ANSYS 有限元分析软件,进行网格划分,由于结构满足对称性,可只取对称轴一侧进行分析,输入的材料特性为:E=2.01×105,μ=0.3,选择八节点四边形单元Plane 183,计算得到抛物线-圆弧型封头的最大应力强度值。
(6)通过集成技术,将Pro/E、ANSYS 集成到Isight 软件流程中。Isight 提供优化设计流程、数据处理以及优化方法,自动化批量运行整个流程,重复计算后得到优化后的抛物线-圆弧型封头结构参数。
3.5 优化结果及分析
优化结束后,提取所有计算得到的抛物线-圆弧型封头应力强度最大值,可以得到随着优化变量b 的变化,抛物线-圆弧型封头的应力强度最大值随之改变,变化趋势是先减小后逐渐增大,最终得到优化变量b 是2.24 的优化结果。优化结果及应力强度云图如图8~10 所示。

图8 优化结果Fig.8 Optimized result

图9 优化后应力强度云图Fig.9 Stress intensity cloud map after optimization

图10 优化中出现的最大应力强度云图Fig.10 Maximum stress intensity cloud map appearing in the optimization
综上可知,优化后的应力强度比优化前减小了4.27%,比优化过程中最大工况减小了16.67%。优化变量的变化对于抛物线-圆弧型封头与筒体组成的整体结构产生了很大的影响。
4 线性化分析
按照JB 4732—1995《钢制压力容器—分析设计标准》,对抛物线-圆弧型封头进行应力评定。在封头上选择封头顶部位置、应力强度最大值位置以及远离连接位置的筒体位置进行应力评定,各个路径的示意图如图11 所示。

图11 应力评定路径示意图Fig.11 Schematic diagram of the stress assessment path

表5 抛物线-圆弧型封头评定路径与结果Table 5 Assessment path and results of the parabolic-arc head
通过对室温下Q345R 材料封头的应力分析可以看出,抛物线-圆弧型封头的评定路径中,路径PATH2 是应力强度最大的路径,原因是封头的过渡段受到了球壳与圆柱壳体的边缘应力影响,导致出现了无法避免的应力集中现象,但是仍然满足许用极限要求。
5 结论
本文以整体应力强度最小化为优化目标,对抛物线-圆弧型封头的结构参数进行优化分析,得到最优的抛物线-圆弧型封头模型尺寸数据。对优化后的抛物线-圆弧型封头根据标准进行了应力线性化评定,为抛物线-圆弧型封头的设计提供一种分析依据。
在交界处假定的曲率连续性条件,由于抛物线-圆弧型封头中抛物线旋转壳体、圆柱壳和球壳的变形规律不同,导致连接区域仍然会发生应力分布突变。利用数值优化对抛物线-圆弧型封头的抛物线变量参数进行优化,优化后抛物线-圆弧型封头的应力强度最多可降低16.67%,优化变量的变化对于抛物线-圆弧型封头与筒体组成的整体结构产生了很大的影响。
