冰区船舶换热器中两相流传热特性的仿真与实验研究*

徐 立 刘宗强 刘冠辰 黄长绪

(武汉理工大学能源与动力工程学院 武汉 430063)

0 引 言

随着北极航道的开通，极地冰区船舶的关键建造技术已成为全球造船业的热点[1].北极航道具有缩短航程，节省成本的优点，相对于传统的商业路线，运输时间、燃料消耗减少[2-3].但是，极地海洋环境恶劣，对通航在北极冰区的船舶性能也提出了更高的要求[4].在船舶的航行过程中，冰晶颗粒会夹杂在海水里形成海水-冰晶两相流，当进入到船舶换热器的管程中容易造成冰堵，极大地影响航行安全.

目前，针对船舶换热管道内海水-冰晶两相流的传热研究主要集中在对水平圆形换热管内的流动传热研究.Zhang等[5]得出相变对传热的贡献沿流动方向减小，导致局部传热系数降低；Li等[6]得出冰浆的传热性能很大程度上取决于流速和含冰率，而热流密度对Nu数的影响很小；Bordet等[7]运用欧拉-欧拉双流体模型，分析湍流状态下的冰浆在水平管道中的等温流动，探讨了不同条件下冰晶体积分数及速度沿轴向与径向分布特征.虽然目前已有诸多学者对水平圆形管道内海水-冰晶两相流的流动传热过程进行了研究，但关于海水-冰晶两相流流动传热实验测试仍然很匮乏.而且，诸多学者研究所选取的基本边界条件、固液两相流本身物性参数等也不尽相同，同时更多的只是通过仿真进行分析入口流速、入口含冰率(IPF)对海水-冰晶两相流在管内沿程传热的影响.

于是，针对海水-冰晶两相流在管壳式换热器水平圆形换热管内的热流动过程，通过实验与理论对比分析，不仅从海水-冰晶两相流在管内沿程传热特性进行分析，而且对其在管内局部的传热特性也进行了分析，同时也讨论了局部传热系数在不同入口IPF、流速和热流密度下的变化情况，更加准确地总结出海水-冰晶两相流在管内的传热特性，从而为船舶的设计建造提供理论基础，旨在降低换热器管程发生冰堵的风险，以此更大程度地保障极地船舶在冰区的正常航行.

1 数学模型

在海水-冰晶两相流中，采用基于颗粒动力学理论的欧拉-欧拉双流体模型耦合相间传热传质模型.欧拉-欧拉模型将液相和固相作为相互作用的连续相，分别建立其对应的N-S方程.在数值模拟中，海水-冰晶两相流的流动被视为是湍流和不可压缩流，控制方程有连续性方程、动量守恒方程、能量守恒方程和RNG湍流模型.重点介绍一下相间传热传质模型和颗粒动力学理论.

1.1 相间传热传质模型

通过编译UDF程序，在FLUENT中将传热传质模型嵌入欧拉-欧拉双流体模型，对海水-冰晶两相流的流动与传热特性进行研究.

在流动过程中，管壁的热量主要被管壁附近的海水吸收，进而经过导热、对流等过程传递到主流区.海水吸收了大部分热量，导致海水与冰晶之间形成温差.冰晶吸收相变潜热而融化，使得液相海水与固相冰晶之间发生质量传递.

体积相间传热系数是通过将单个固体颗粒和液体之间的传热系数乘以特定的界面面积得到的，为

(1)

式中：hls为固体颗粒与液体之间的相间传热系数，

(2)

其中：Pr为普朗特数；Res为雷诺数.

1.2 颗粒动力学理论

将固体颗粒作为致密气体分子处理，颗粒-颗粒碰撞引起的固体颗粒运动假定为气体中分子的热运动.用颗粒拟温度θs来描述固体颗粒的波动能量，其数学描述为

(3)

(4)

式中：kθs为温度扩散系数，描述了固相与液相之间速度波动量转换关系,

(5)

其中：ess为颗粒-颗粒碰撞恢复系数，ess=0.9.

ζsl=-3θsγsl

(6)

其中：ζsl为液相与固相的能量转换.

(7)

式中：Ψθs为固体相碰撞而导致的内部能量耗散率;ps为固体相压力,

(8)

2 数值方法

采用商业CFD软件FLUENT模拟计算海水-冰晶两相流在管壳式换热器换热管内的传热特性，数值计算模型采用非稳态求解，所有控制方程都通过有限体积积分法进行离散化，采用二阶离散格式，通过Phase Coupled SIMPLE算法求解离散方程.此外，将时间步长指定为0.001 s以促进收敛，当收敛速度足够快时，时间步长增加到0.005 s，以加速计算.当所有残差均小于1.0×10-4时达到收敛.同时设置观察出口处海水的平均温度和冰晶的体积分数，当其不随时间变化时，认为数值解已经稳定.

2.1 管道参数及网格划分

根据换热器行业标准，选取换热管的外径d=25 mm，取换热管长度为2 m，建立的三维模型采用六面体单元进行网格划分，满足计算精度的要求，见图1.因为网格单元数增加到一定数量时，计算结果不再随网格数量的增加而改变或改变非常小，此时的网格数量即满足数值计算的网格独立性要求，故选择网格数量735 000进行数值计算.

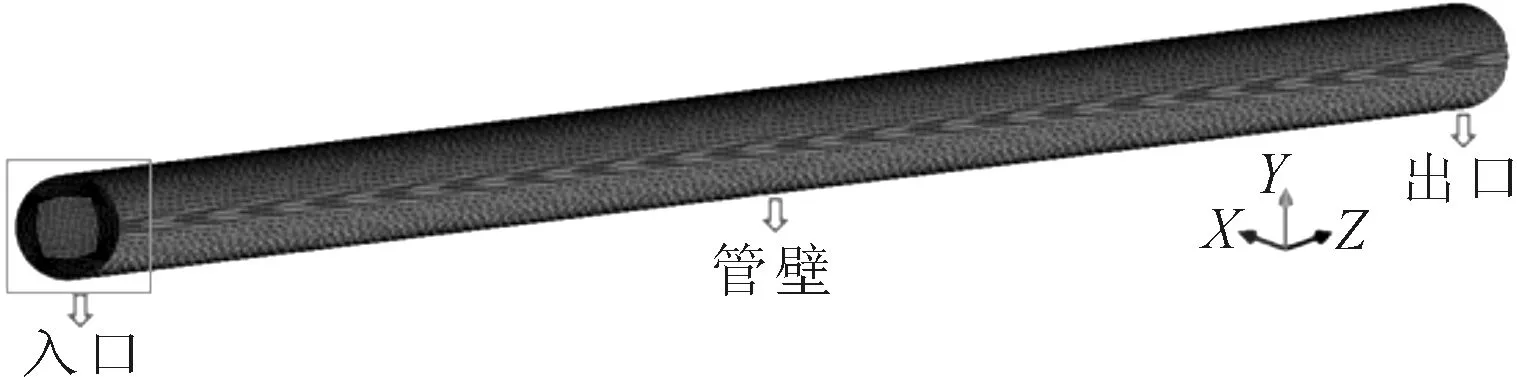
图1 管道三维网格示意图

2.2 海水与冰晶基本热物理性质

极地船航行时，据“永盛轮”近年的北极实地航行科学考察报告及相关资料和国标的船舶海水管系流速设计规范要求，北极夏季海水平均盐度约为3.5%[8]，海水盐度为3.5%时海水与冰晶的热物性参数见表1[9-10].

表1 海水与冰晶的热物理性质

2.3 边界和初始条件

对于入口，海水与冰晶均以均匀速度和恒定热流密度进入管道，同时冰晶颗粒在入口管道的截面均匀分布；对于出口，规定压力出口条件；在管壁处，海水采用无滑移条件，冰晶颗粒采用Johnson-Jackson壁面边界条件.海水与冰晶的温度在入口处设置为同一值约271.8 K，并且在数值模拟冰晶的融化特性时，在壁面处采用恒定的热流密度.为了减少计算时间，流场中海水-冰晶两相流的初始条件设置为与入口条件相同.对冰晶颗粒形状简化为平均直径0.5 mm的球状颗粒.

3 实验装置

海水-冰晶两相流流动传热实验测试系统原理图见图2.主要由冰浆制取与储存系统、冰浆流动传热实验测试段与数据采集系统组成.

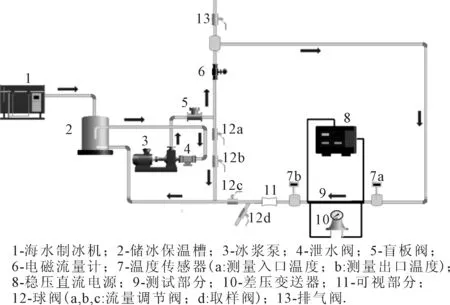
图2 海水-冰晶两相流流动传热实验测试系统原理图

3.1 实验装置中测试仪器的精度

采用智能型电磁流量计测量管路中海水-冰晶两相流的体积流量，安装在水流向上的垂直管道上.型号为LDG-DN15，流量范围0～15 m3/h，精度等级为1.0 FS.对电磁流量计进行校检，校验装置为DCZZ-DN6—DN3000，校验精度为1.0 FS.

采用智能差压变送器测量测试管道中海水-冰晶两相流浆体的压降.型号为TRD-3351，测量范围为0～10 kPa，精度等级为±0.2% FS.

数据采集系统采用彩色流量无纸记录仪，仪器的型号为HN-VGA-E，测量精度为0.2% FS±1 d.

3.2 实验误差分析

在实验中，需要对海水-冰晶两相流的流速、含冰率和压降等测量参数进行误差分析.其中，海水-冰晶两相流的流速与压降属于可以直接测量的参数，海水-冰晶两相流的含冰率属于间接测量参数.在实验测试过程中，直接测量参数的误差主要受偶然误差与系统误差的影响.偶然误差服从置信水平为95%的t分布，系统误差由实验中采用的仪器设备精度决定.

4 结果分析

4.1 海水-冰晶两相流在管内的沿程传热特性

以入口含冰率10%，入口平均速度1.5 m/s，管壁恒定热流密度3.3 kW/m2为例，进行海水-冰晶两相流在管内的沿程传热特性实验研究.同时，进行数值模拟.其数值计算条件与实验相同.图3～6为实验及数值模拟结果.

图3 海水-冰晶两相流及管壁沿流动方向的温度变化

由图3可知，实验测量结果和数值计算结果均表明海水的平均温度Tl比冰晶颗粒温度Ts、海水-冰晶两相流的平均温度Tsl升高的快.实际上，海水-冰晶两相流在管内的流动过程中，由管壁传递的热量主要被壁面附近的液相海水吸收，然后经过导热作用以及对流作用从管壁传至管内部的冰浆体.而海水-冰晶两相流的温升由其吸收的热量、冰晶颗粒的传热传质率,以及冰晶发生相变的时间决定.

在测试管中沿流动方向轴向距离0～800 mm之间，由实验测量获得的测试管壁面局部平均温度沿流动方向迅速升高，而局部平均管壁温度沿流动方向变化梯度则逐渐下降，这是由于加载在管壁面恒定热流密度的加热作用.图3中的从区域I至区域Ⅱ，最终在轴向距离约为800 mm之后稳定在某一定值附近，这是由管道入口区域海水-冰晶两相流的热流动发展造成的.根据实验结果可知，该热流发展的入口长度为800 mm.

在数值计算中由于海水-冰晶两相流的热流动发展略慢，热流发展的入口长度为600 mm.数值计算结果显示，在管道中沿流体流动方向的0～600 mm之间，两相之间的平均传质率也迅速升高，但在区域Ⅱ′中传质率增加的速率低于区域I′，见图4.

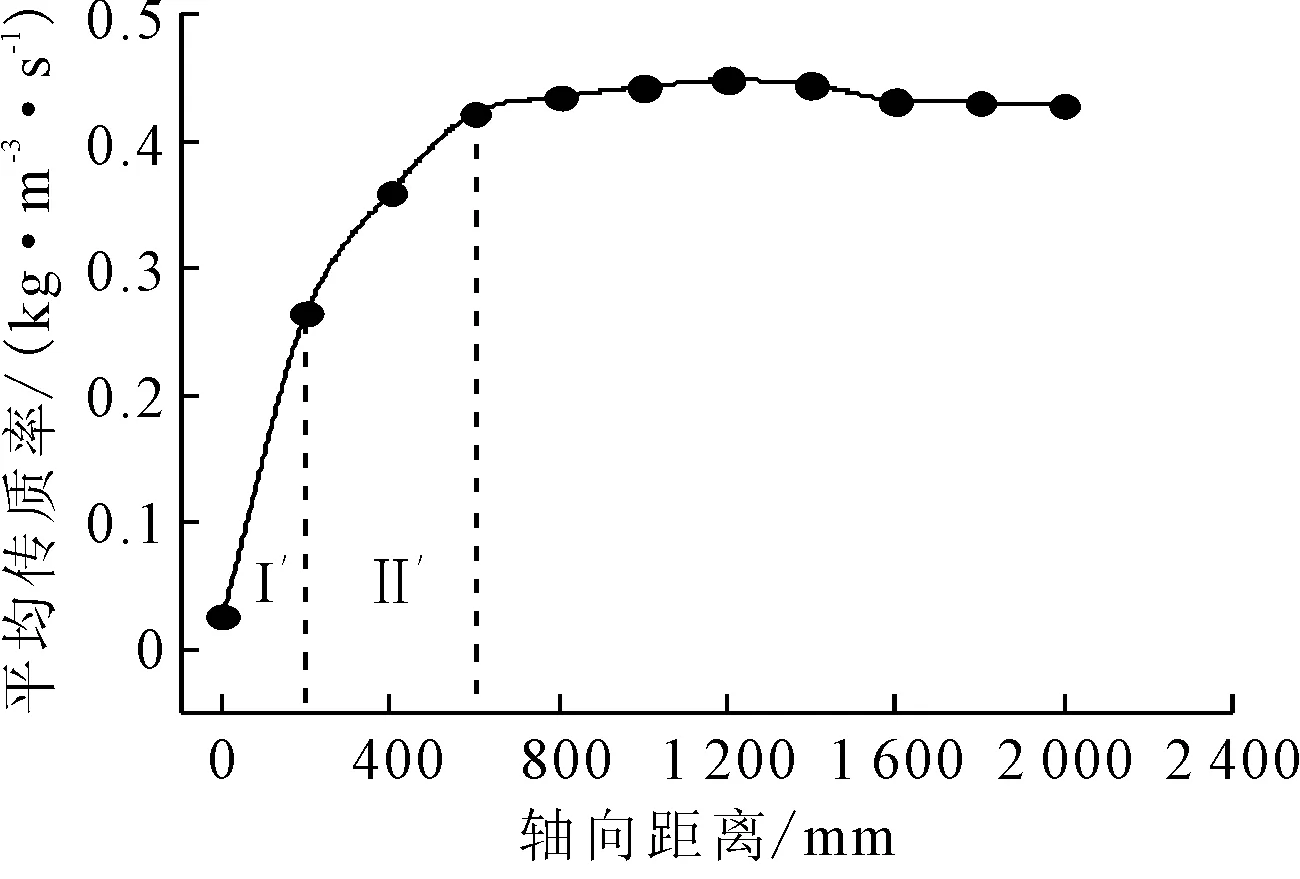
图4 冰晶在管道不同横截面的平均传质率沿程变化

在管道沿流动方向的轴向位置0～600 mm之间，主要是管壁附近的冰晶颗粒发生融化，之后两相之间的传质率基本稳定.此时由于传质率的变化稳定导致冰晶体积分数也恒定下降，见图5.

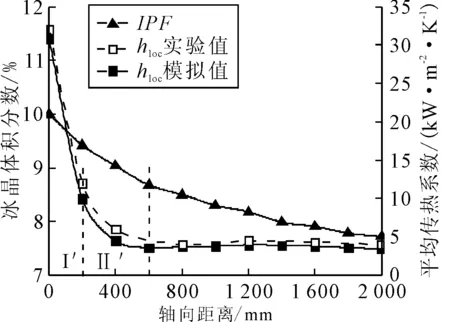
图5 平均局部传热系数及冰晶体积分数沿程变化

由图3可知，在热流动发展的入口长度内海水-冰晶两相流的平均温度比壁温度增加得慢得多.因此，图5的管壁和海水-冰晶两相流之间的温差迅速增加，导致传热系数在热流动发展的入口长度内迅速降低.两相流进入热完全发展区域后，管道中心区域的冰晶颗粒也发生融化.在图5中，实验测量结果和数值计算结果均表明，海水-冰晶两相流的平均局部传热系数在热完全发展区域接近为恒定，这主要是由于在该区域中，冰晶颗粒体积分数减少量仅为热流动发展入口区域的一半左右，并且流体在管内一次流动时间很短，因此冰晶相变引起的强化传热对海水-冰晶两相流的平均局部传热系数的影响很小，导致流体的传热系数在热完全发展区域基本恒定.

图6为沿流动方向，在管道不同横截面处冰晶的体积分数分布及对应流体温度分布的数值计算结果.

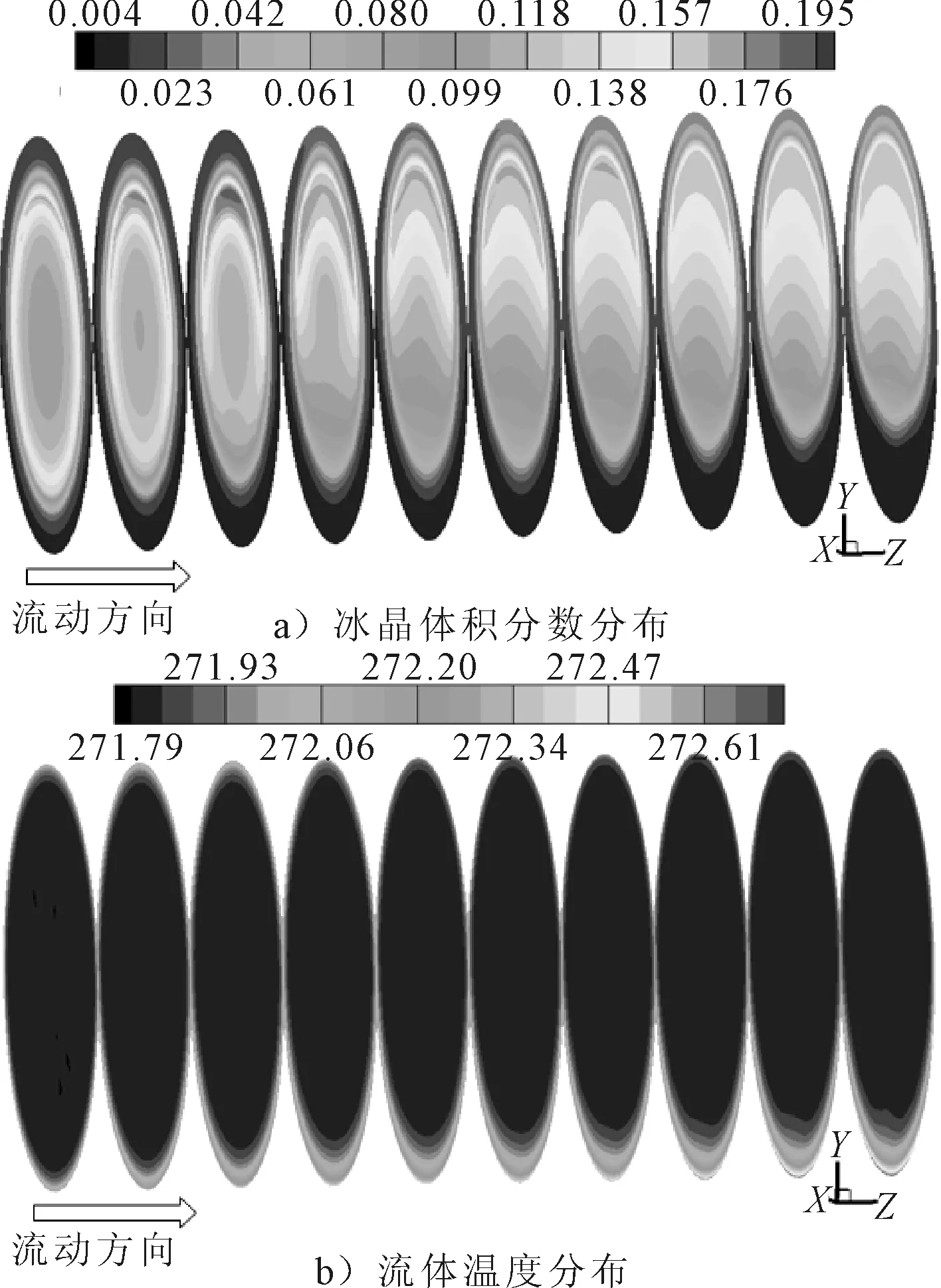
图6 沿流动方向，冰晶的体积分数分布及温度分布

当海水-冰晶两相流由测试管入口进入后，在壁面恒定热流密度的作用下，管道近壁的流体温升变化显著，并且此处的径向温度梯度较大，而海水-冰晶两相流的温度在主流区域较低，呈现均匀分布特性.图6a)中沿流动方向的轴向位置Z=200 mm即第一个横截面温度边界层较薄，壁面和流体之间的传热作用较强，导致海水-冰晶两相流的局部平均传热系数较高.随着海水-冰晶两相流的不断流动发展，冰晶的体积分数分布发生非均质性分布，进而影响到管壁附近流体温度的分布，可以看到由于冰晶向上悬浮分布导致管壁底部近壁区域的温度边界层显著增加，顶部近壁区域的温度边界层减小，海水-冰晶两相流的局部平均传热系数减小.沿流动方向海水-冰晶两相流的局部平均传热系数逐渐减小，最终趋于恒定，与实验获得的结果基本一致，此时海水-冰晶两相流的流动达到完全发展状态.

当海水-冰晶两相流在管内的流动达到完全发展后，由于加载在壁面恒定热流密度的作用，近壁附近的流体温度会继续增加，但其与主流区中海水-冰晶两相流的温度差基本恒定，同时温度边界层厚度的变化也较小.另外在完全发展阶段，在不同截面冰晶的体积分数分布基本稳定，但因冰晶颗粒吸热融化，冰晶在截面的体积分数平均值仍逐渐降低.

4.2 海水-冰晶两相流在管内的局部传热特性

4.2.1入口含冰率与速度对局部传热系数的影响

图7为不同的入口含冰率与速度的工况下，海水-冰晶两相流与管壁局部表面传热系数的实验与数值计算结果.由图7可知，在入口含冰率为0～20%时采用欧拉-欧拉双流体模型耦合传热传质模型获得的结果与实验测量的结果基本吻合.而在入口含冰率为30%时数值计算结果与实验结果有较大的偏差，这是由两方面原因导致：①入口含冰率为30%的数值计算过程中，由于冰晶颗粒与管壁的碰撞剧烈，使得冰晶颗粒往管道主流区域聚集的情况比实验更加显著；②入口含冰率较高时，冰浆泵运行的不稳定性增大.

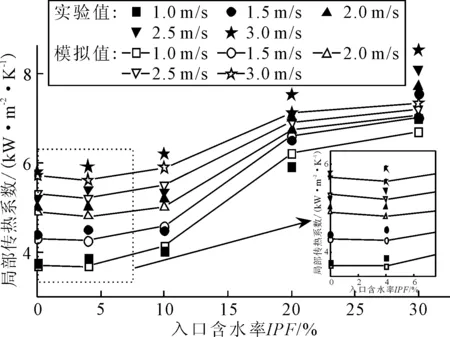
图7 海水-冰晶两相流的局部传热系数

由图7可知，在入口含冰率为0%～10%之间时，局部传热系数随入口含冰率的增加而略微增加；当入口含冰率大于10%之后，局部传热系数随入口含冰率的增加而呈现快速增加，并且速度较低时传热系数增加的更快；入口含冰率从20%增加至30%时，传热系数值增加的不明显.在入口IPF=0%～30%,U=1～3 m/s范围内，局部平均传热系数随入口流速和含冰率增加先增加最终趋于稳定.结果表明，传热系数不会随速度与含冰率的增加而一直增大.这主要是由海水-冰晶两相流在管内的流型决定.相对于较高含冰率时速度对传热的影响，含冰率较低时速度对传热的影响更显著.

4.2.2热流密度对局部传热系数的影响

图8为热流密度为0.5 ～3.0 kW/m2，入口含冰率为10%与20%时局部传热系数随速度变化的实验值与数值计算值.由图8可知，当热流密度值增大时，局部传热系数随之增加.当热流密度值从0.5 kW/m2增加到3.0 kW/m2时，局部传热系数增加约10%～30%.在热流密度一定的情况下，局部传热系数随速度的增加而增加的速率逐渐降低，当平均速度达到3.0 kW/m2时，热流密度从0.5 kW/m2增加到3.0 kW/m2，局部传热系数并没有明显的增加.在入口含冰率为10%时，见图8a)，局部传热系数受热流密度的影响变化较大.而当入口含冰率为20%时，热流密度的变化对局部传热系数的影响变小，见图8b).

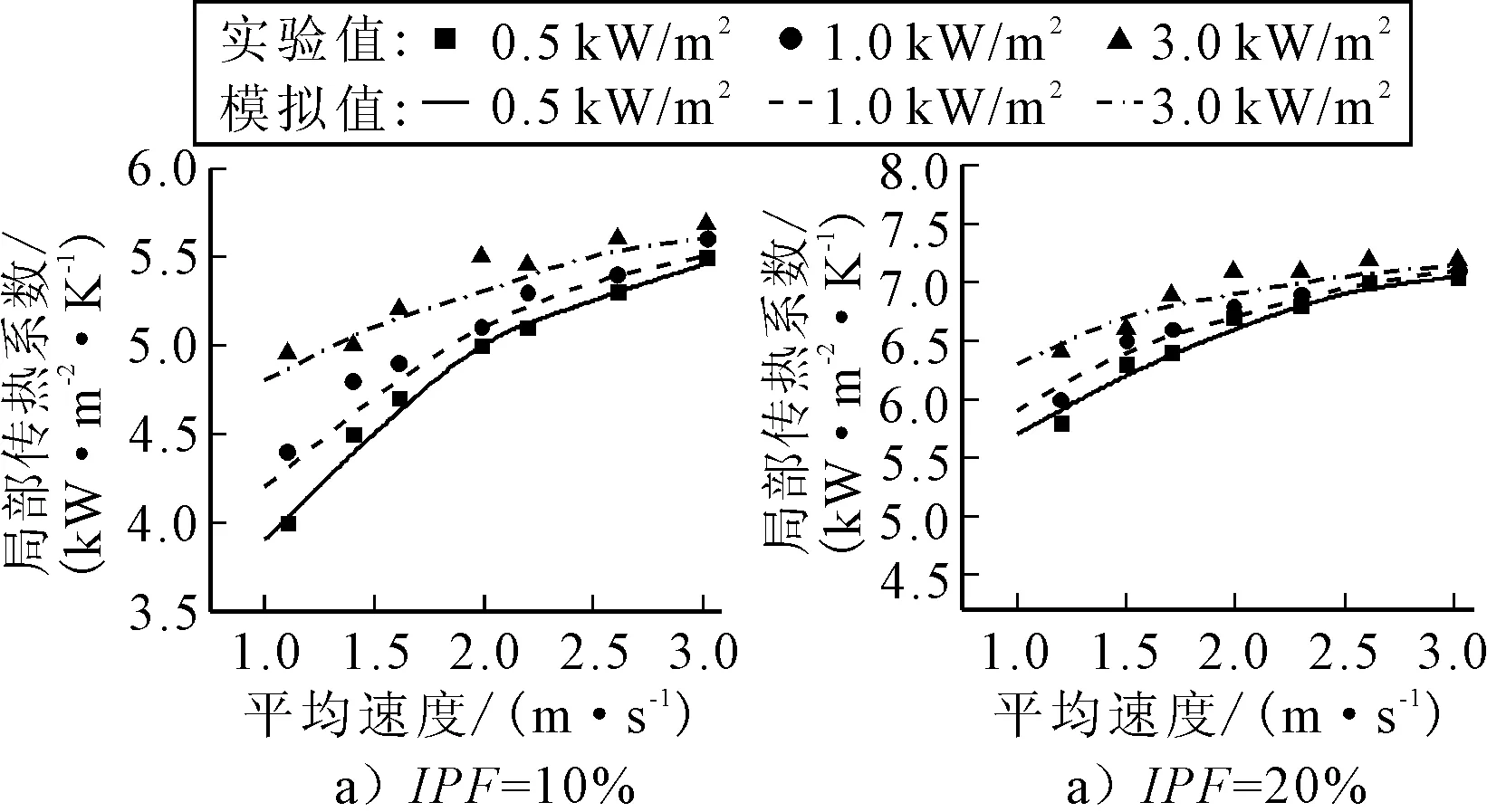
图8 热流密度对局部传热系数的影响

5 结 论

1) 海水-冰晶两相流在管内的流动传热包括入口段和完全发展段.在入口段，局部传热系数沿流动方向迅速降低；在热完全发展区域，局部传热系数接近为恒定.

2) 冰晶与海水之间的传热传质过程随入口流速、含冰率以及热流密度的增大而增强.

3) 在入口IPF=0%～30%,U=1～3 m/s范围内，局部平均传热系数随入口流速和入口含冰率的增加先增加最终趋于稳定.

4) 传热系数不会随速度与含冰率的增加而一直增大，相对于较高含冰率时速度对传热的影响，含冰率较低时速度对传热的影响更显著.

5) 当热流密度值增大时，局部传热系数随之增加.热流密度值从0.5 kW/m2增加到3.0 kW/m2时，局部传热系数增加约10%～30%.