基于状态频率记忆神经网络的短时交通流预测*

余敬柳 陈 鹏 谢静敏

(武汉理工大学交通学院1) 武汉 430063) (广东华路交通科技有限公司2) 广州 510550)

0 引 言

短时交通流预测主要是依据当前道路交通流量的变化规律以及特性进行准确和实时的预测，能够合理的推断出未来短时间内的交通状况.近年来，采用机器学习方式预测短时交通流成为研究的热点，神经网络作为主要的机器学习算法越来越被研究人员所关注.

Chan等[1]应用小波理论建立的神经网络模型预测短时交通流，相比传统的BP神经网络获得更好的预测效果.Fusco等[2]将具体的贝叶斯网络与人工神经网络进行融合建模来预测短时交通流，并利用浮动车大样本数据进行验证.王体迎等[3]提出了一种基于门限递归单元循环神经网络的短时交通流量预测方法，可有效的利用“序列信息”建模，同时进行了实例验证.谈苗苗[4]提出了一种基于LSTM循环神经网络和灰色模型相结合的短时交通流预测模型.乔松林等[5]针对交通流的特点，提出了一种结合LSTM长短时记忆神经网络与支持向量机结合的交通流预测模型.罗向龙等[6]提出了一种基于KNN-LSTM的短时交通流预测方法.刘念等[7]采用长短时记忆神经网络模型进行交通流预测.王祥雪等[8]构建了一种基于LSTM-RNN的城市快速路短时交通流预测模型.LSTM神经网络虽然能够解决神经网络典型的梯度消失或爆炸的问题，但是经典的LSTM神经网络仅仅以时间信号的状态向量为记忆元(memory cell)进行建模，而忽略了另一个重要维度频率，针对LSTM的这种不足，研究者提出了一种基于状态-频率记忆神经网络的预测方法.Hu等[9-10]提出了一种依据傅里叶变换的状态-频率记忆循环神经网络.目前，状态-频率记忆神经网络在交通领域应用较少，在已有的应用研究中，状态-频率记忆神经网络用于预测时并没有用到数据去噪方法对数据进行去噪处理，从而降低了预测的精度.

本文采用状态频率记忆神经网络模型预测短时交通流，利用小波分析对交通流原始数据进行去噪处理，并以python2.7为开发平台，通过OpenITS获得合肥市某交叉口的历史交通流数据并进行分析建模，验证本文所提短时交通流预测模型的实用性.

1 状态频率记忆神经网络

1.1 状态频率记忆神经网络结构

状态频率记忆(state frequency memory，SFM)神经网络具有一般循环神经网络的优点，即在神经网络结构中，其隐藏层之间的节点是有连接的，它能够接受当前时间点输入层输入的信息也能够接受上一时间点输入层输入的信息，同时SFM神经网络具有输入层、隐藏层、输出层的结构；但是与一般循环神经网络(recurrent neural network，RNN)不同的是，SFM神经网络隐藏层不是以往神经网络中的一个节点而是引入了一个状态-频率矩阵形成结合状态与频率的神经网络记忆单元来保存信息，避免一般循环神经网络会产生梯度消失或者爆炸的缺点.在记忆单元中有三个门单元，分别为遗忘门、输入门,以及输出门，其中遗忘门的作用为控制信息流入记忆单元、输入门的作用为控制信息流入记忆单元、输出门的作用为控制信息流出神经元.

SFM神经网络结构见图1.

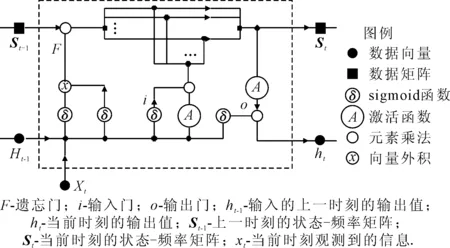
图1 SFM神经网络结构

1.2 状态频率记忆神经网络算法

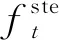
(1)

(2)

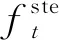
(3)

式中：Wste状态遗忘门的权值；xt为输入的序列数据；Uste为状态遗忘门中隐藏层上一个时刻到当前时刻的权值；ht-1为t-1时刻隐藏层的输出；bste状态遗忘门的偏置项；Wfre频率遗忘门的权值；Ufre为频率遗忘门中隐藏层上一个时刻到当前时刻的权值；bfre为频率遗忘门中的偏置项.

2) 输入门的计算 输入门决定了能够在当前时刻保存多少输入的信息到单元状态，计算方法为

it=sigmoid(Wixt+Uiht-1+bi)

(4)

式中：it为t时刻输入门的输出值；Wi为输入门的权值；Ui为输入门中隐藏层上一个时刻到当前时刻的权值；bi为隐藏层的偏置项.

接下来计算描述当前输入的单元状态，计算方法为

(5)

ct=tanh (Atua+ba)

(6)

状态-频率矩阵St的幅度At的计算方法见式(7)；相位∠St的计算方法见式(8).

(7)

(8)

状态-频率矩阵St可以分为实部IMSt和虚部RESt，其计算方法为

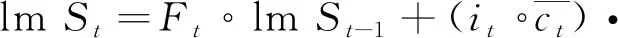
[sin(ω1t),…,sin(ωK)]

(9)

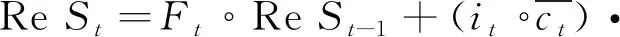
[cos(ω1t),…,cos(ωKt)]

(10)

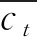
3) 输出门的计算 输出门决定了在当前时刻能够保存多少信息流出神经元，通过输出门ot调节允许从记忆单元输出的信息，计算方法为

ot=sigmoid(Woxt+Uoht-1+Voct+bo) (11)

ht=ot∘ct

(12)

式中：ot为输出门调节允许从存储单元输出的信息；ht为t时刻隐藏层的输出值；Wo为输出门的权重；Uo为输出门中隐藏层上一个时刻到当前时刻的权重；bo为输出门的偏置项.

4) 状态-频率矩阵更新 状态-频率矩阵的更新规则为

(13)

式中：[ejw1t,wjw2t,…,wjwkt]为状态序列上的K个频率分量的傅里叶基；输入门it调节流入当前存储单元的新信息量；St为t时刻的状态-频率矩阵；Ft为t时刻遗忘门的输出值；St-1为t-1时刻的状态-频率矩阵.

5) 激活函数 在循环神经网络中采用激活函数一般为sigmoid和tanh函数.激活函数sigmoid计算方法见式(14)，sigmoid函数形如S形曲线，它的输出映射在(0，1)之间；当输入值趋于正无穷时，输出值趋于1；当输入值趋于负无穷时，输出值趋于0；当输入值为0.5时，输出值为0.5.激活函数tanh计算方法见式(15)，tanh函数输出映射在(-1，1)之间；当输入值为0时，输出值也为0；当输入值趋于正无穷时，输出值趋于1；当输入值趋于负无穷时，输出值趋于-1.

(14)

(15)

2 短时交通流预测流程及步骤

本文采用SFM状态-频率记忆神经网络对交叉口的短时交通流进行预测，主要包括以下步骤.

1) 得到时间间隔内历史交通流数据 将预测的指定时间间隔内的多个历史交通流数据按照一定时间间隔进行累加，得到汇总后历史交通流数据，其中所述汇总后的历史交通流数据Q为

(16)

Q=[Q1,Q2,…,Qn]

(17)

式中：i为时间间隔的序号；j为时间间隔内时间的序号；n为时间间隔的数量；m为时间间隔内时间的数量；Qi为汇总后的第i段时间间隔内的交通流量；gi,j为第i段时间间隔的第j-1至j段时间内的交通流量；Q为多段时间间隔的交通流量汇总后组成的时间序列；即汇总后的历史交通流数据.

2) 预处理 首先采用小波分析[3]对汇总的历史交通流数据进行数据去噪，然后将去噪的数据进行归一化处理，其目的在于使处理之后的历史交通流数据值域在区间[-1，1]内，具体的方法为

(18)

式中：Q′为归一化处理之后的历史交通流数据；Qmin为汇总去噪后的历史交通流数据Q的最小值；Qmax为汇总去噪的历史交通流数据Q的最大值；Qqz为汇总去噪后的历史交通流数据.

3) 设置模型参数 合理的设定状态-频率记忆神经网络预测模型的参数；包括设定输入层节点数量为d1，隐藏层(的隐藏层节点数量为d2，输出层节点数量为d3，频率维为K，迭代次数为iter，学习率为lr，批量大小为batch_size，激活函数；损失函数loss；优化器参数.

4) 模型预测交通流 将归一化预处理的历史交通流数据划分为训练集数据Qtra、验证集数据Qval以及测试集数据Qtest；利用训练数据集，在根据步骤3设定合理参数的状态-频率记忆神经网络的模型上进行训练.将验证集的数据输入模型modz，并计算状态-频率记忆神经网络模型在验证集上的误差，误差式为

(19)

式中：M为模型输出数据；Q′为输入的验证集数据.

选择验证集上误差最小的状态-频率记忆神经网络模型作为状态-频率记忆神经网络交通流预测模型，其中误差寻优方法为

MSE=min|MSEz|

(20)

5) 模型预测结果评估 利用最终确定的交通流预测模型预测指定时间间隔的交通流，对模型输出的相应的输出数据A进行逆归一化处理，见式(21)，并评估预测误差.

式中：A′为逆归一化之后的数据，即下一指定时间间隔交通流数据预测值；Qmin为汇总后的历史交通流数据Q中的最小值；Qmax为汇总后的历史交通流数据Q中的最大值；Q为汇总后的历史交通流数据；A为已训练的交通流预测模型对下一指定时间间隔交通流数据的归一化预测值.

进行逆归一化处理之后，通过计算预测交通流的平均相对误差以及均方误差，可以评价短时交通流预测的效果.平均相对误差及均方误差的计算方法为

(22)

(23)

3 实例验证

3.1 数据来源及预处理

以合肥市某交叉口为例，利用微波检测器共获得了30 d交叉口的交通流数据.同时，本文以5 min时间间隔为例，预测该交叉口的短时交通流.

1) 数据去噪 在matlab中采用小波分析的wavedec函数对交通流数据进行分解，同时采用db6函数对数据进行三层分解；采用软阈值进行信噪分离；采用waverec函数重构信号，从而完成数据去噪.

2) 数据训练集、验证集和测试集的划分 以30 d中前24 d的交通流数据作为模型的训练集数据、以后续3 d的交通流数据为验证集数据、以最后3 d的交通流数据作为模型的测试集数据.

3.2 参数设定

建立具有三层结构的SFM模型，其隐藏层的神经元为一层，隐藏神经元的节点数为50.同时设定模型的迭代次数iter=1 200，设定模型的频率维K=10，设定学习率lr=0.01，设置损失函数lose为MSE，`优化器参数为RMSprop，激活函数为sigmoid函数及tanh函数.

3.3 预测结果

设定SFM状态-频率记忆神经网络预测模型的参数之后，以5 min时间间隔为例，对该交叉口的交通流量进行预测，状态-频率记忆神经网络预测模型所预测的交叉口交通流量的结果与交叉口实际交通流的对比分别见图2.

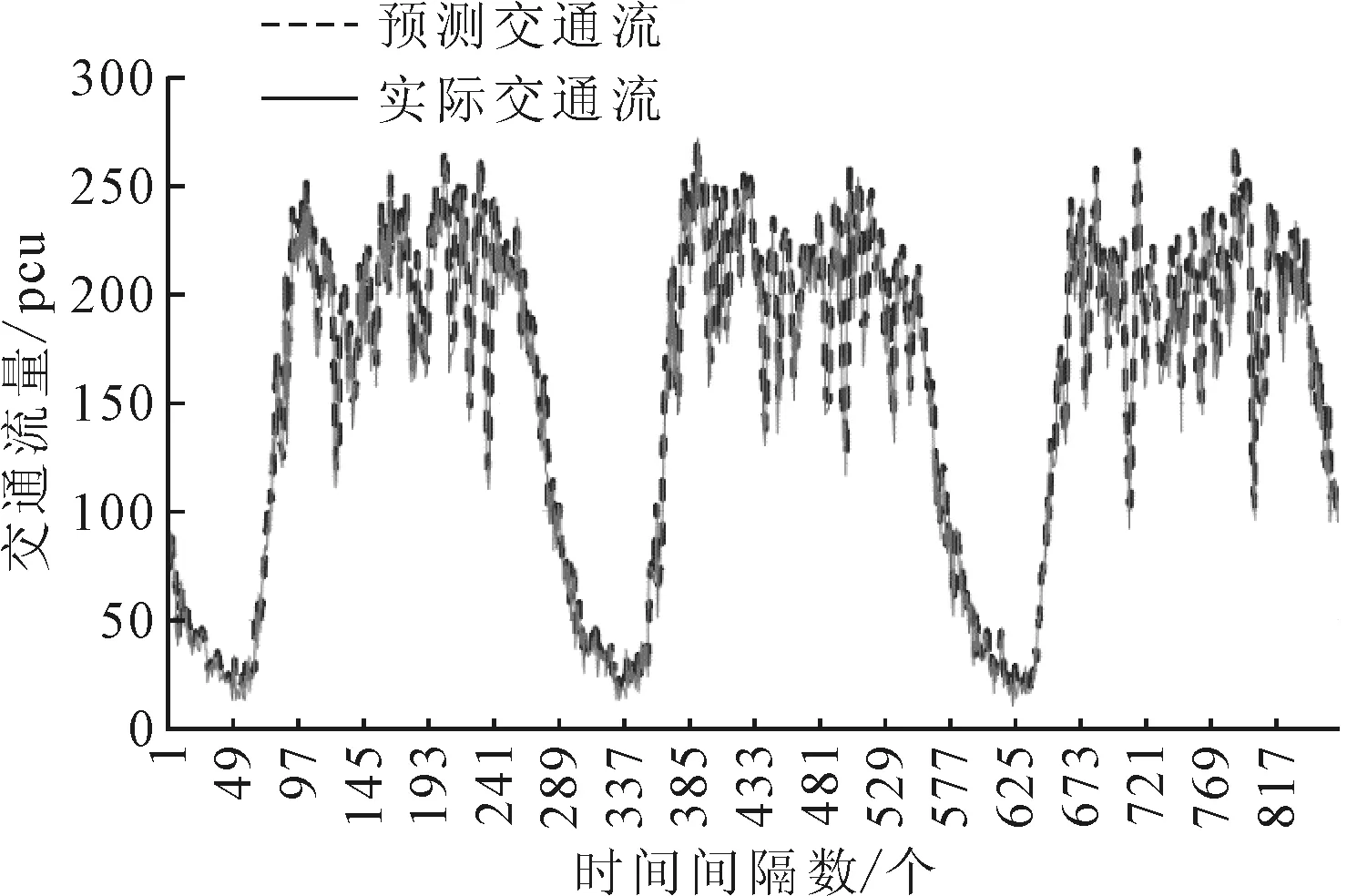
图2 5 min时间间隔预测结果

3.4 不同预测方法比较

为了验证本文所提状态-频率记忆神经网络短时交通流预测方法的有效性，本文分别采用三次指数平滑法和BP神经网络分别以5 min时间间隔时长对该交叉口进行短时交通流预测，并分别计算出其平均相对误差以及均方误差；同时与本文所提方法产生的均方差和平均相对误差进行比较，对比的结果见表1.

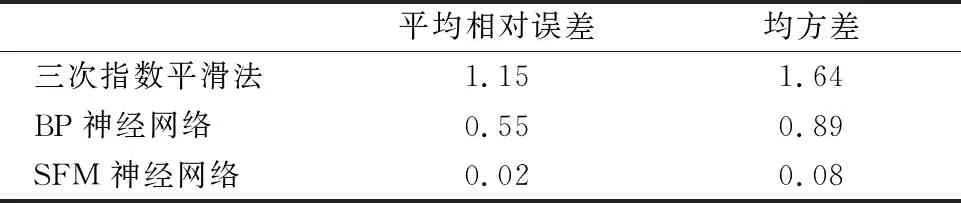
表1 不同预测方法误差对比

由表1可知，与三次指数平滑法以及BP神经网络相比，本文所提SFM状态频率记忆神经网络的短时交通流预测效果是最好的.采用SFM神经网络预测短时交通流的平均相对误差和均方差远小于使用BP神经网络和三次指数平滑法来预测短时交通流的误差.因此,可以验证SFM神经网络预测交叉口的短时交通流具有较好的效果.

4 结 束 语

综合考虑交通流信息的状态以及频率两个维度，提出了基于SFM状态频率记忆神经网络的短时交通流预测模型.通过获取合肥市某交叉口的实际数据进行预测，并通过与指数平滑法以及BP神经网络等方法进行对比，可以发现，SFM状态-频率记忆神经网络预测交通流的误差是最低的，验证了该模型能够提高短时交通流预测的精度，证明了该模型的有效性.同时，本文研究没有考虑到天气等影响因素，因此在未来的研究中如何考虑天气等因素对短时交通流预测影响是很有必要的.