考虑供需变化的城市出租车运力投放优化研究*

蔡 赫 赵 昕

(交通运输部科学研究院 北京 100029)

0 引 言

城市出租车运力合理投放至关重要，区域内出租车数量投放过多会导致空驶率上升，增加运输成本；过少则出现供不应求，增加乘客候车时间，降低服务质量.城市中不同区域功能不同，居民出行需求变化规律呈现差异性，如：居住区出行需求表现为“朝发夕至”，而商业区则表现为“朝至夕发”.同时，出租车的地理位置也会因乘客出行在各区域间发生变化.因此，考虑乘车需求与出租车供给随时间变化情况，研究如何合理投放城市出租车运力具有重要的理论意义和实用价值.

关于城市出租车运力投放优化问题的，目前国内外有较多研究.Daganzo[1]基于排队论理论，利用乘客最大候车时间等指标研究确定出租车最优运力规模；杨海等[2]建立了出租车服务模型用以描述空驶出租车搜索乘客行为，并计算得到了平衡状态下的出租车合理运力规模；陆建等[3]考虑出租车空驶率、有效行驶里程、运营速度等因素计算出城市出租车合理运力规模；边杨等[4]通过建立出租车网络均衡模型，描述了出租车规模与搜索时间、乘客等候时间的关系；Jinshi[5]从城市出租车供需影响因素的角度，考虑城市经济发展水平、人口数量、拥堵情况、环境等多方面确定城市出租车合理规模.Morelira等[6]利用GPS运行数据，在分析乘客出行需求的基础上给出了出租车运力投放的计算方法；黎冬平[7]则通过仿真的方法分析出行者与出租车之间的相互作用，据此计算出租车上客区的合理数量.此外，随着网约车的发展，近年来不少学者对网约车背景下城市出租车的运力调度进行了研究[8-10].

以往研究中主要从静态角度分析出租车出行需求与供给关系，并进行运力调度优化，本文以居民候车时间最少为目标，考虑出租车需求与供给随时间的动态变化，提出城市各区域清晨出租车运力投放的建议值.

1 问题描述与建模

1.1 考虑供需变化的城市出租车布局问题

出租车运力合理投放问题是现代社会亟待解决的重要问题，不合理的投放加剧了城市道路压力，同时影响乘客出行体验.影响出租车运力投放的因素众多，其中最重要的是各区域采用出租车出行的需求.影响区域居民出行特征的因素中，城市建设用地类型至关重要.按照文献[11]中规定，我国城市建设用地类型分为八类：居住用地(R)、公共管理与公共服务用地(A)、商业服务业设施用地(B)、工业用地(M)、物流仓储用地(W)、道路与交通设施用地(S)、公共设施用地(U)，以及绿地广场用地(G).

区域内用地类型不同，居民出行特征存在差异，如居住类型用地到商业用地的出行需求表现为“朝发夕至”(交通发生需求随时间逐渐减少)，商业用地到居住用地的出行需求表现为“朝至夕发”(交通发生需求随时间逐渐增加)，见图1.这里，假设出租车出行需求与全方式出行需求成正比，变化趋势相同，用dij(t)为区域i到区域j的采用出租车出行的交通发生需求，随时间t变化.

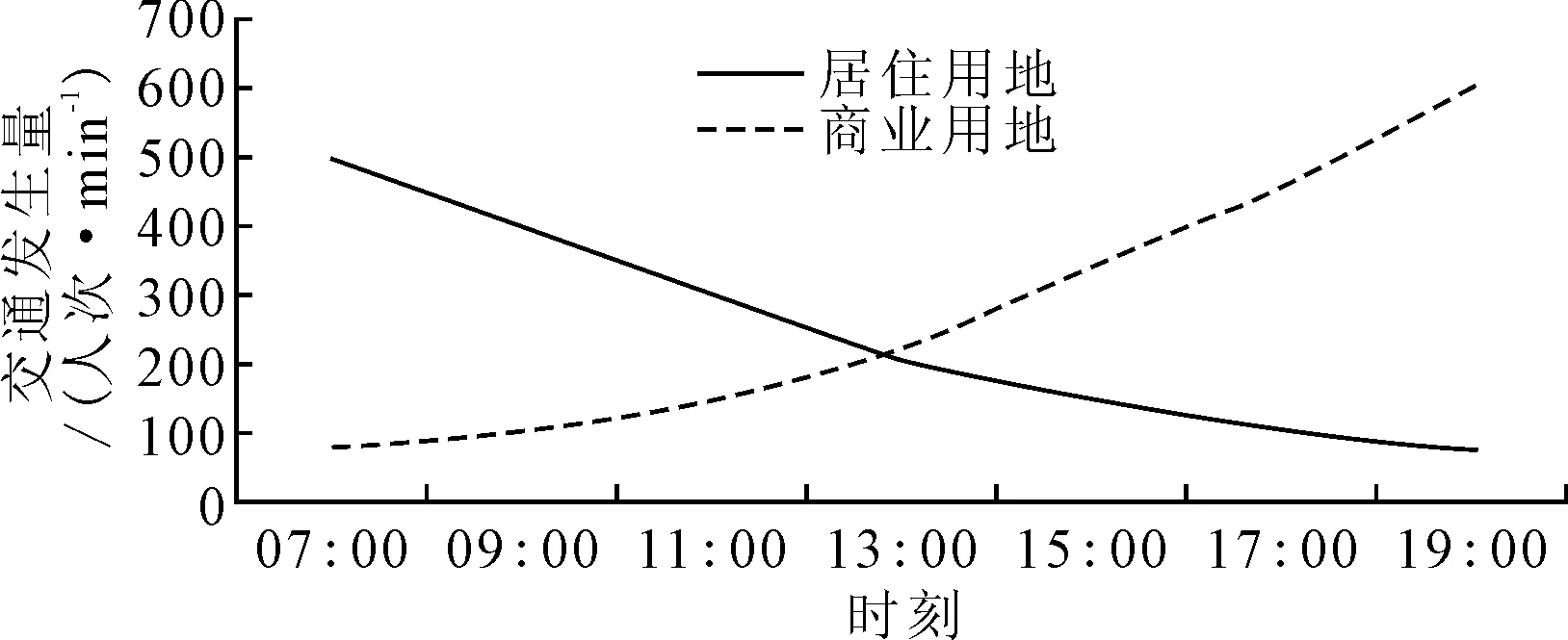
图1 居住用地与商业用地居民出行需求时变示意图

1 d之中，出租车受乘客乘车出行影响，其空间位置在各区域间不断变化，见图2.区域i中出租车的数量可表示为ni(t)，随时间t变化.

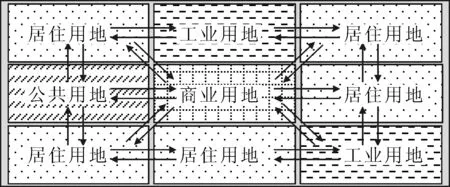
图2 不同区域之间出租车流向示意图

区域i中的出租车数量ni(t)的变化受两种流量影响：从其他区域j驶入区域i的流量vji(t)，以及从区域i驶出到区域j的流量vij(t).则时间Δt内，区域i中出租车的数量变化为

(1)

区域i到区域j的出租车流量vij(t)取决于四种因素影响：区域i到区域j的出租车需求，出租车载客人数，区域i中出租车的数量，以及区域i与区域j之间的行驶时间.公式为

(2)

式中：λ为出租车平均载客人数；Tij为区域i到区域j的平均行驶时间.可以看出，当需求的出租车数量小于区域i中实际拥有的出租车数量时，vij(t)正比于需求出租车数量；当需求的出租车数量大于区域i中实际拥有的出租车数量时，vij(t)正比于区域i中实际的出租车数量.vij(t)反比于行驶时间.将式(2)带入式(1)中，取Δt为无限小，变换后可得

(3)

因此，通过求解微分方程，得到ni(t)表达式.

1.2 模型建立

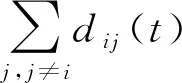
(4)

式中：tstart为起始时间；tend为终止时间；θ为等车时间系数，取值越大表征同样规模需求和出租车供给的情况下等车时间越长，通常受城市可达性影响较大，城市可达性越高，θ取值越低.其中dij(t)可结合区域用地性质与图1预先设定或根据调研拟合得出.假设城市出租车运力总量为N，起始时间区域i投放出租车运力的比例为ρi(∑ρi=1)，则

ni(tstart)=ρiN

(5)

将式(3)与式(5)带入式(4)中，即可得到关于ρi的多元方程，进而进行最优化求解.

1.3 求解算法

从上面的模型可以看出，出租车运力投放优化问题是一个多元非线性最优化问题.为方便求解，本文采用遗传算法的方法，将操作对象ρi看作是一个生物群体，经过多代进化后选择出优秀个体作为系统的最优解.

2 模拟计算与结果分析

2.1 数值模拟与计算

假设某城市可分为两个区域：居住区(编号：1)、商业区(编号：2).区域间采用出租车出行的交通发生需求分别满足线性规律，如式(6)和式(7)所示(单位：人次/min)：

d12(t)=-0.2t+200

(5)

d21(t)=0.1t+70

(6)

式中：时间t取值为[0, 840]，每一刻度时间间隔1 min.tstart=0为起始时间(本算例中假设为6:00)；tend=840为终止时间(本算例中假设为20:00).

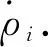
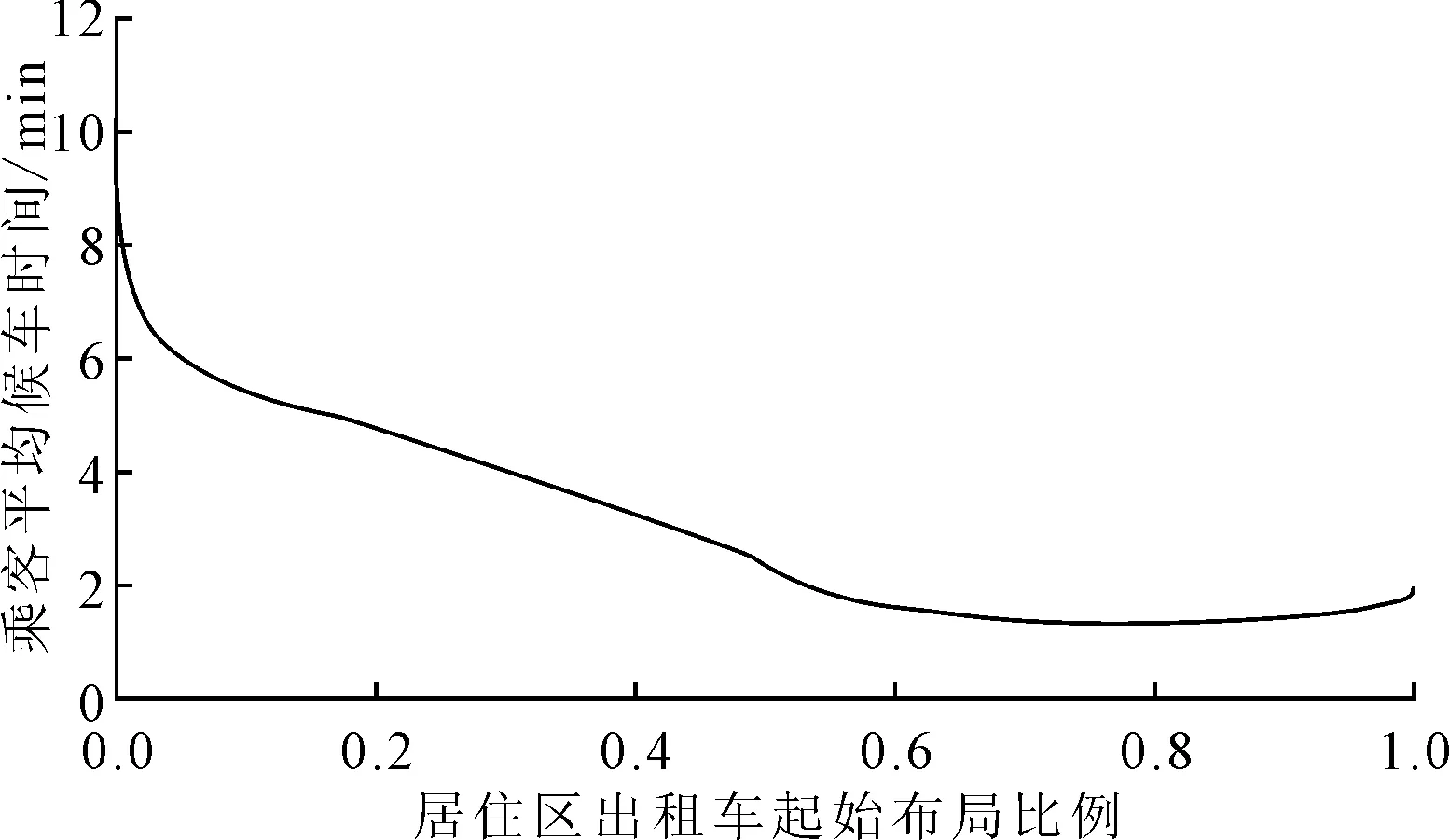
图3 乘客平均候车时间与居住区出租车起始布局比例关系

由图3可知，居住区起始时间(清晨06:00)的出租车运力投放比例将会影响到全天乘客平均候车时间.若居住区投放的出租车过少，则居住区内的出租车供给不能满足乘客出行需求，乘客等车时间增加；当居住区投放的出租车过多，则相应的商业区布局出租车过少，从全局角度考虑，同样会使得乘客候车时间增加.本示例中，当居住区布局比例达79%时，乘客平均候车时间最低，此时为1.3 min.此时，城市出租车布局方案为：清晨06:00时在居住区投放790辆出租车，在商业区投放210辆出租车.

2.2 城市出租车合理规模分析

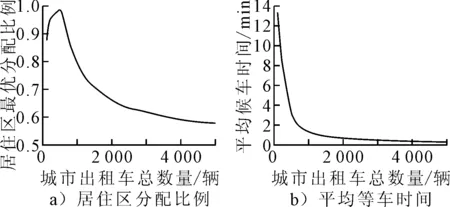
图4 出租车总体规模与最优分配比例及乘客平均等车时间的关系

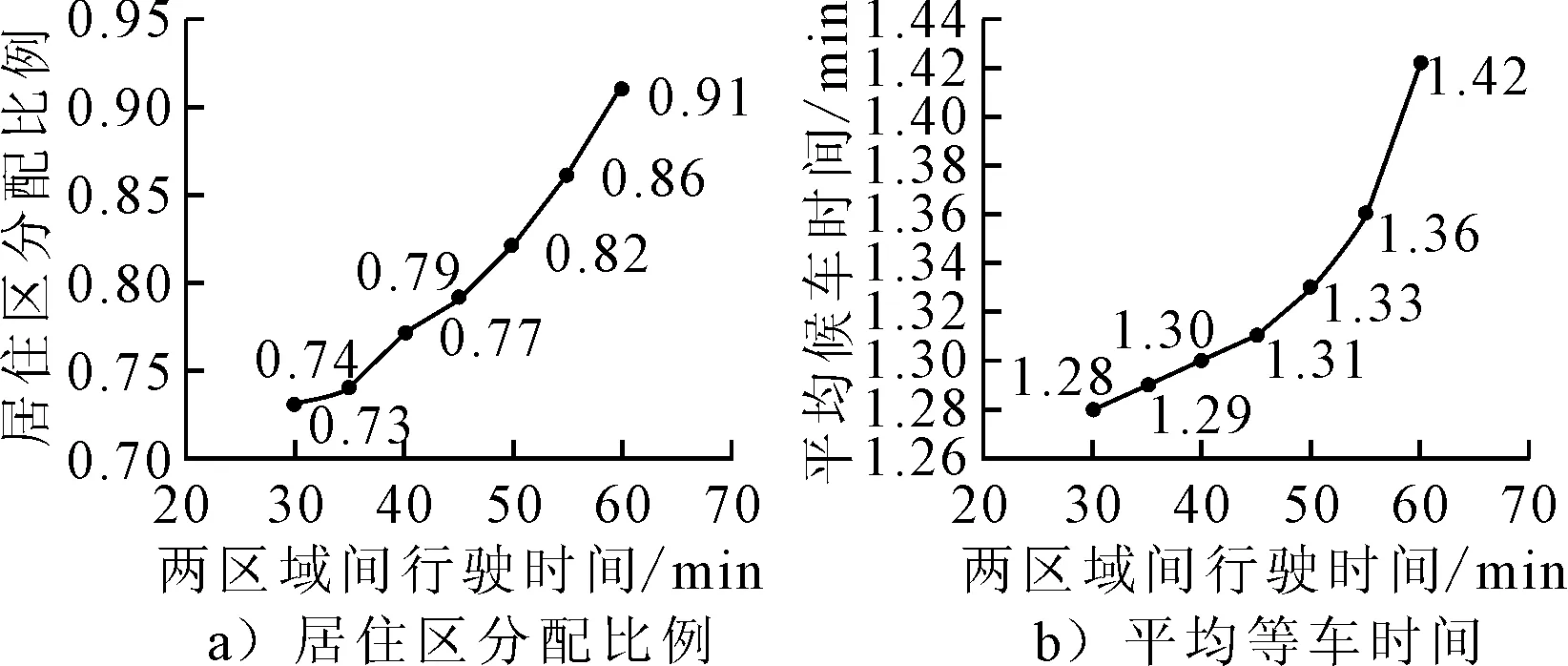
由图4a)可知，当城市出租车运力总量较低时，居住区投放比例相对较高，超过85%. 此时，虽然居住区投放比例很高，但由于运力总量较低，出租车处于供不应求的状态，即：式(2)中dij(t)/λ>ni(t).故随着总体规模N的增大，居住区最优投放比例继续增加，以满足居住区的出行需求，降低乘客候车时间.当出租车运力总量超过一定数值时，即：式(2)中dij(t)/λ

图4b)可知，随着出租车运力总量增加，平均候车时间逐渐降低，边际效益递减.明显看出，当出租车运力总量达到400辆时，平均候车时间约为5 min；当出租车运力总量达到700辆时，可保证平均候车时间在2 min以内；而要使平均候车时间降低至1 min以内，出租车运力总量需达到1 300辆.决策者可根据平均候车时间作为出租车服务水平，规划出租车运力总量的合理规模，本案例中建议运力总量为700辆.

2.3 两区域之间行驶时间对计算结果的影响分析

将区域间行驶时间分别设定为30，35，40，45，50，55，60 min，保持其他参数不便，计算最优投放比例与乘客平均候车时间，结果见图5.

图5 两区域间行驶时间与最优分配比例及乘客平均等车时间的关系

由图5可知，随着两区域间行驶时间的增加，最优运力投放比例中居住区的比例逐渐提高，平均候车时间也逐渐提高.这是由于行驶时间增加导致在途行驶出租车数量增加，空驶出租车数量降低，相当于出租车运力总量降低.因此，对应图4中的关系，当出租车规模在1 000辆左右变化时，居住区分配比例及乘客平均等车时间均随出租车运力总量降低而升高.

3 结 论

1) 当城市出租车运力投放总量较小时，应倾向于投放在清晨出行需求较高的区域(如居住区).

2) 随着城市出租车运力投放总量的增大，应增大在其他区域(如商业区)的投放比例.

3) 乘客平均候车时间随城市出租车运力投放总量的增大而降低，且边际效益递减.

本研究中尚未考虑行驶时间动态变化对优化结果的影响，后续研究将进一步探讨.