多级奇异值分解和SG的通信雷达信号降噪方法*
2020-08-26位秀雷刘树勇
位秀雷 刘树勇
(中国人民解放军91404部队1) 秦皇岛 066000) (海军工程大学舰船与海洋学院2) 武汉 430033)
0 引 言
雷达已应用于地面、空中、海上和太空,地面雷达主要用来探测、定位和跟踪空中目标,不仅在军事各个方面得到应用,同时在民用雷达方面也发挥着日益增长的作用[1-3].然而雷达回波信号在接受过程中受到内部噪声、地杂波和外部干扰等噪声的影响,导致目标检测结果出现偏差,甚至影响目标识别的正确判断,使我方指挥者难以做出正确决策,并且雷达信号和噪声频带部分甚至全部混叠,传统的冲击响应滤波器无法依据差频信号频域分布的特点对滤波器参数进行自适应修改,难以有效实现信噪分离[4-5].
目前较为常用的雷达信号降噪方法有小波分析、经验模态分解,以及相关延伸算法.小波阈值降噪方法,采用卷积方法提取高低频细节,计算复杂且阈值处理采取一刀切的方法,会丢失很多目标特征信息,雷达回波信号目标信息属于微弱信号,其重要特征失真,很难提取有效信息[6],做出准确识别,且小波阈值处理效果会受到小波基函数、分解层数以及阈值选择的影响;EMD是一种无需先验知识的信号处理方法,其分解完全依赖信号本身,但是,在局部干扰下,EMD分解得到的本征模态分量(intrinsic mode function,IMF)会发生畸变[7],且EMD本身有缺陷,如模式混叠、端点效应等[8],文献[9]利用无偏自相关运算,计算各IMF能量,确定出有用信号贡献率最大的IMF,进行FMCW雷达信号特征提取,该方法自适应高,但是会导致其他IMF分量有用细节流失.奇异值分解(singular value decomposition,SVD)是一种有效的非线性信号处理方法并应用于多个领域信号处理[10],该方法将原始信号分解为由大到小的奇异值,表示信号的奇异值要大于噪声的奇异值,通过确定有效秩阶次,将表示信号的奇异值重构实现降噪,其关键是如何有效确定分解后的有效秩阶次[11],为此,结合雷达信号本身特性和SVD算法特点,将多级奇异值分解应用到雷达信号降噪处理,通过多次分解,将噪声部分奇异值逐级剔除,保留信号主导的奇异值,然后利用SG滤波算法移动窗口加权平均拟合特性,对信号主导信号进行平滑修正处理,剔除信号毛刺和尖锐,进一步提高信号信噪比,进行了数字仿真与雷达信号处理分析.结果表明:本文方法在有效剔除噪声的同时,减少了原始信号的失真.
1 多级奇异值分解
1.1 奇异值分解
奇异值分解在相空间重构理论基础上,将原始信号x(i),i=1,2,…,n内嵌到维数为L的吸引子轨道D中.
矩阵D表示吸引子在相空间中的演化特性,可表示为D=Dx+Dw.Dx,Dw为干净信号和噪声构成的m×n矩阵,对D进行奇异值分解,获得降序排列奇异值与ui,vi.
D=USVT
(1)
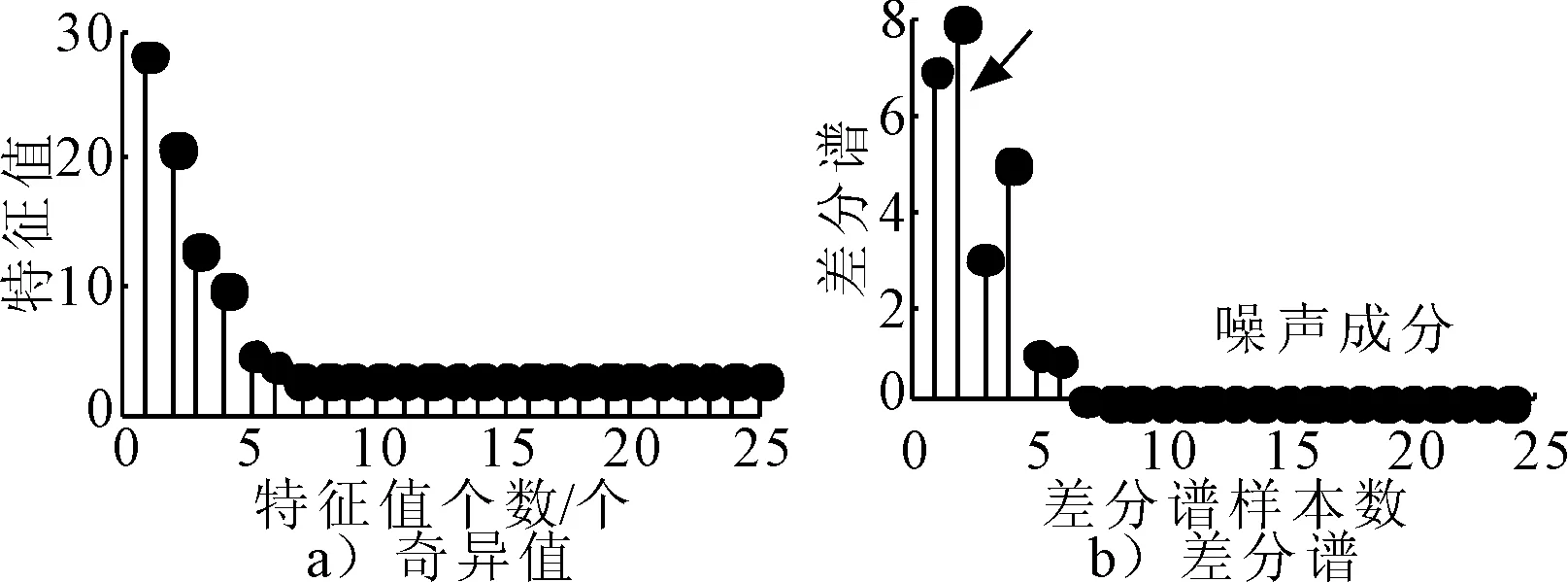
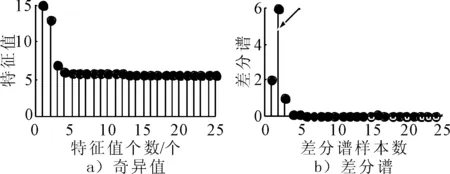
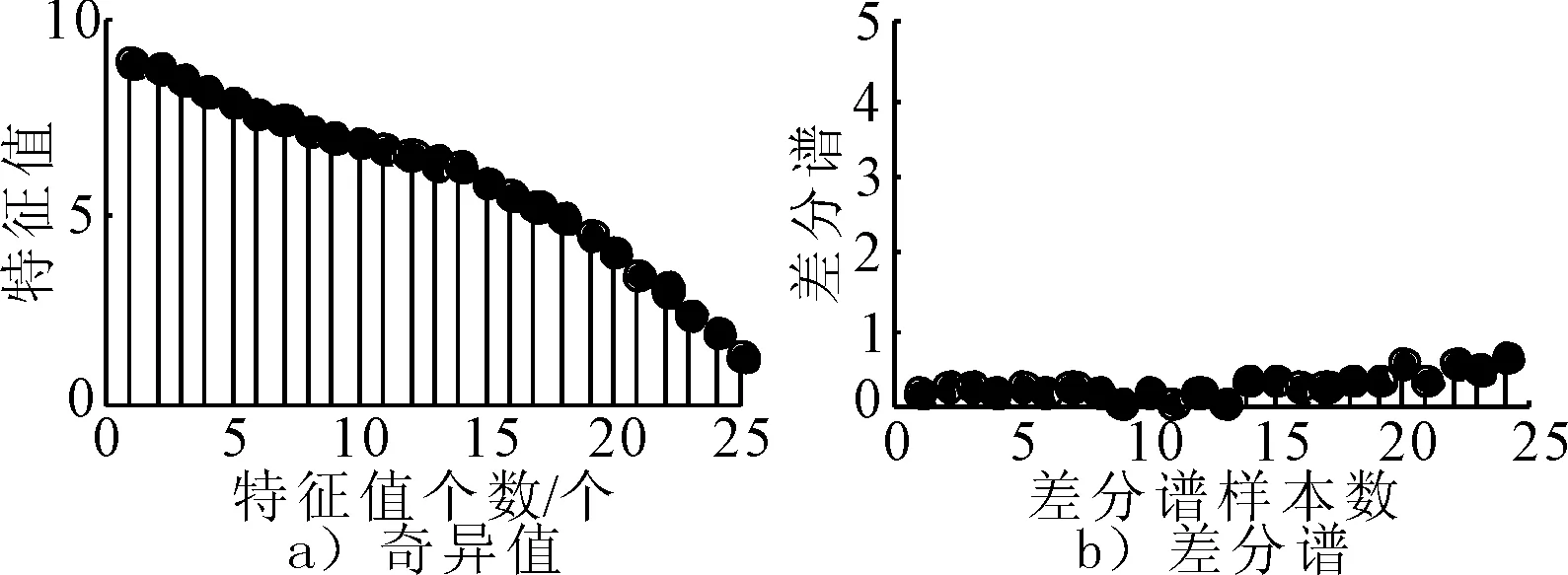
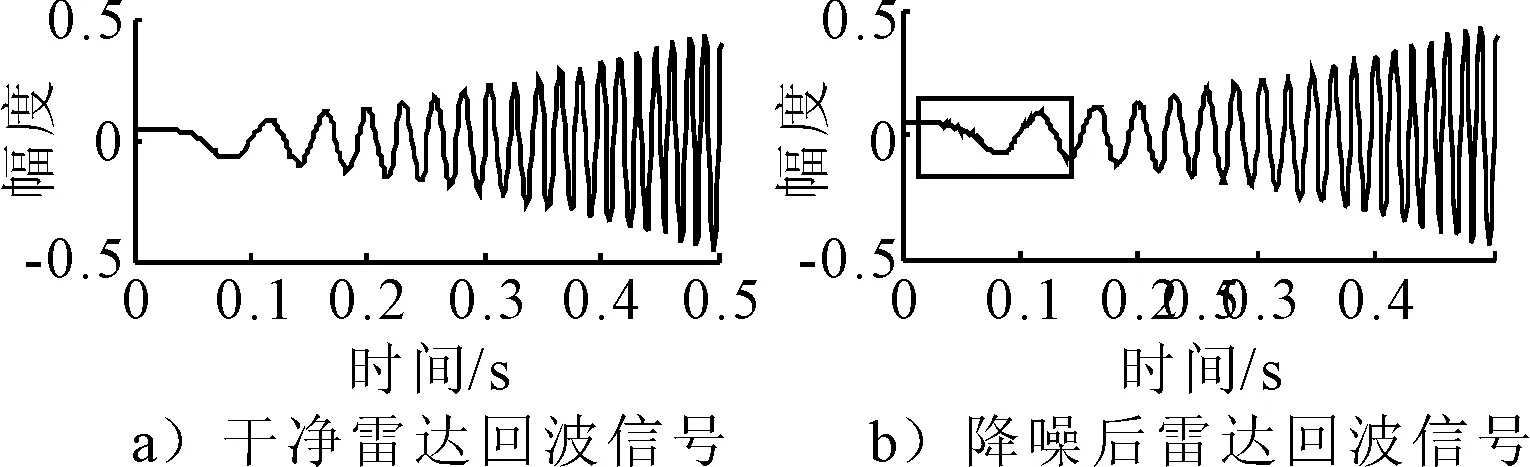
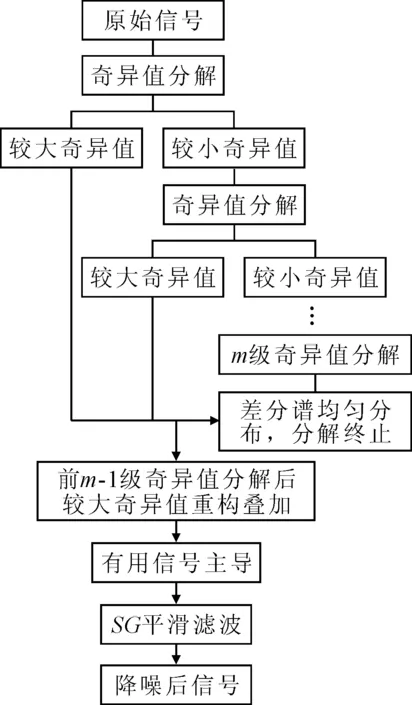
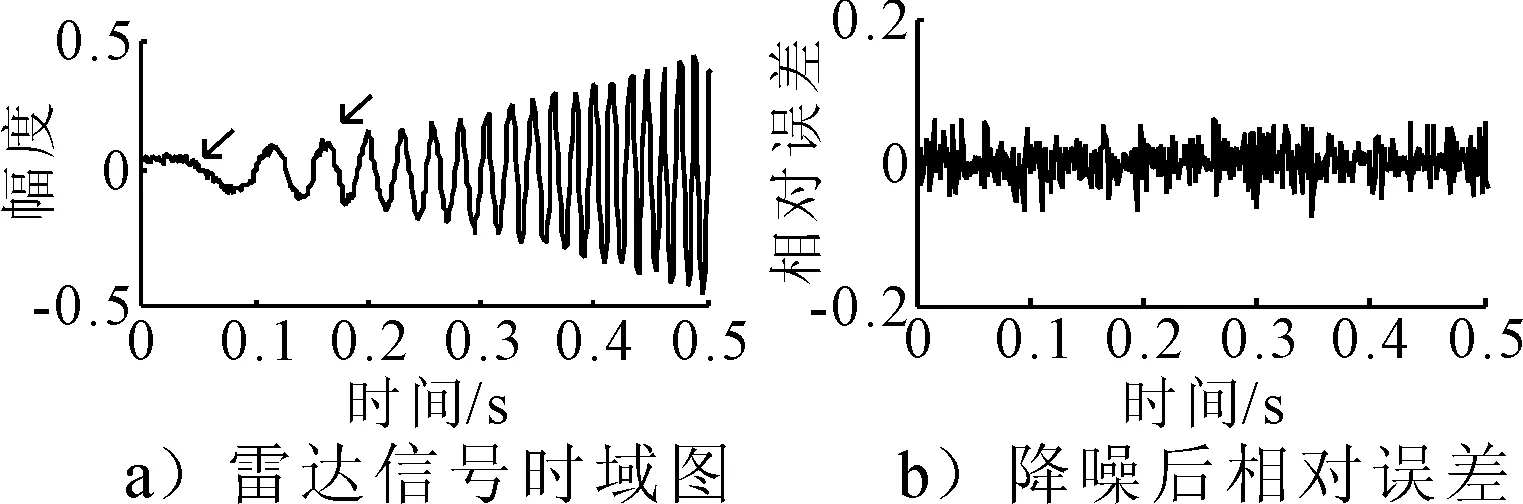
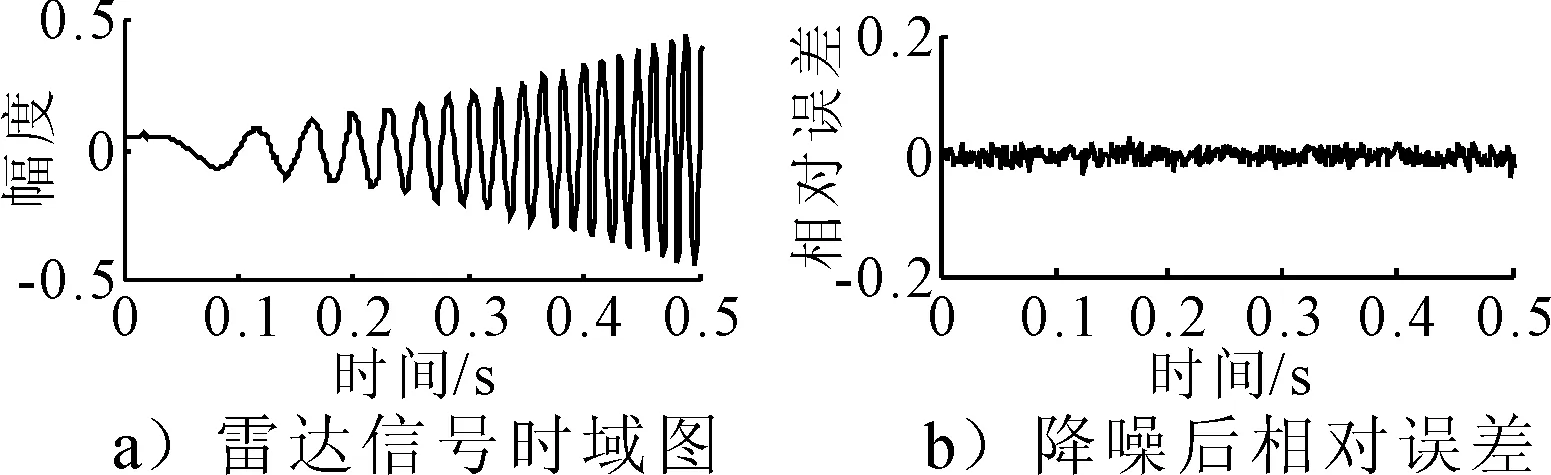
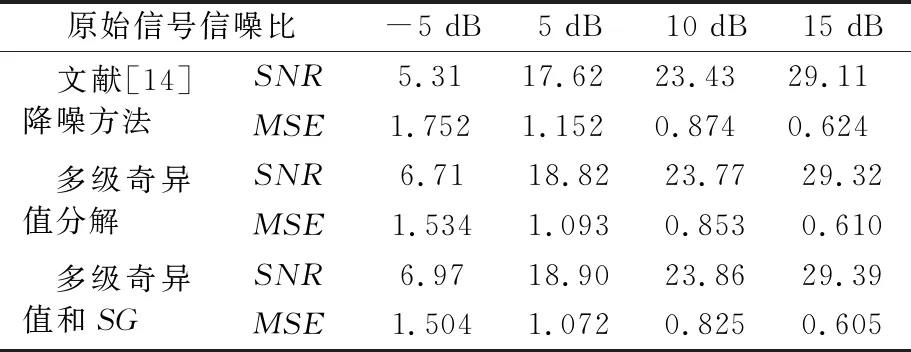
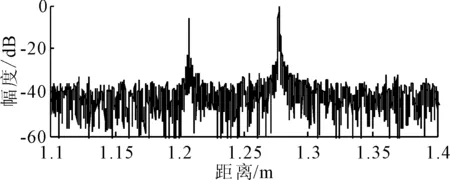
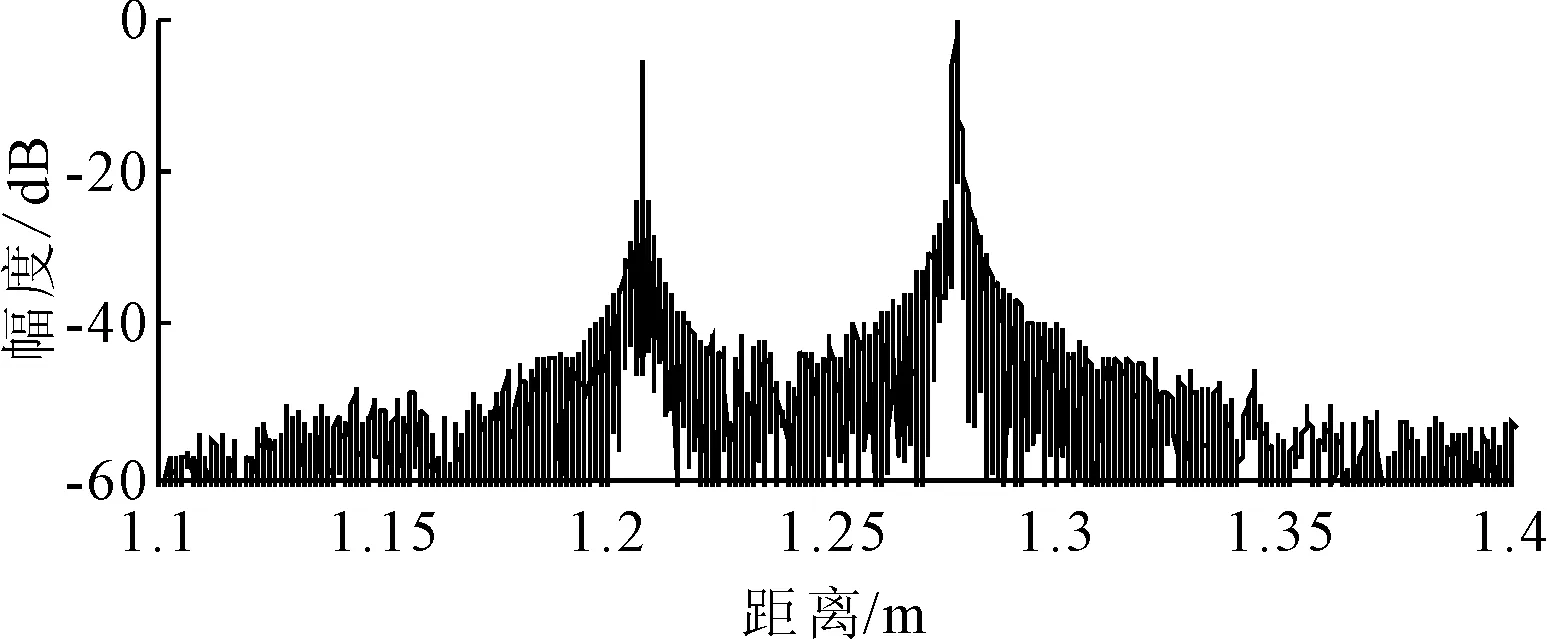
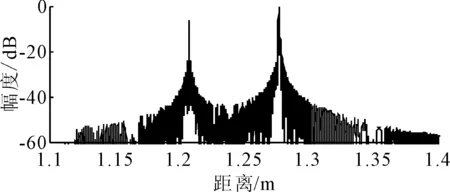
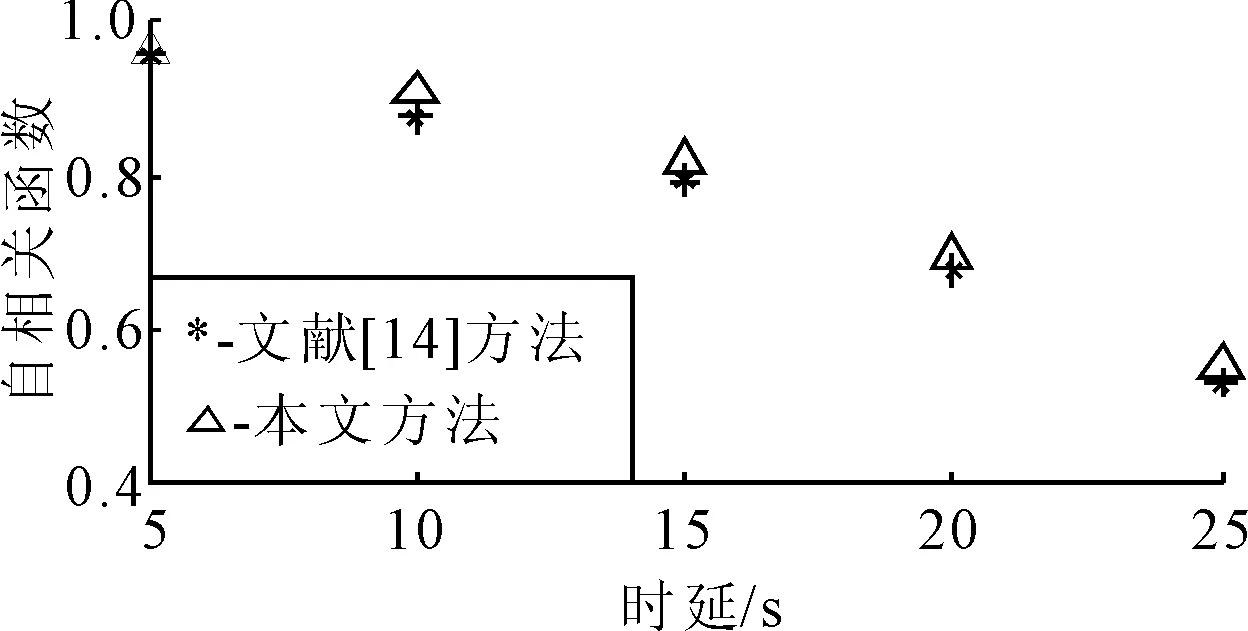
式中:U=[u1,u2,…,un]∈Rn×n,V=[v1,v2,…,vm],S=[diag(σ1,σ2,…,σr),0]或其转置,取决于n>m或n 文献[13]定义奇异值差分谱为 di=σi-σj,j=i+1,i=1,2,…,q (2) 式中:q=min(N-n+1,n)-1. 记差分谱序列D=(d1,d2,…,dq).D的前k个奇异值为信号的真实分量对应的奇异值,第k+1个奇异值起为噪声对应的奇异值,则D的第k个元素dk为差分谱序列的最大峰值,即 k=argmax{peak(di):i=1,2,…,q} (3) 式中:peak(di)为di的峰值.选择前k个奇异值即可重构原信号. 为了避免重构阶次k选取过大或过小导致信号失真或降噪效果不理想,本文采用多级奇异值分解策略实现信号提取.对于高信噪比原始信号,信号占据主导地位,使用文献[14]方法便可得到较好的降噪效果,而对于雷达信号,目标特征比较微弱,隐藏在复杂干扰中,重构阶次的选取就有较困难. 以信噪比为5 dB的雷达回波信号为例,详述多级奇异值分解的实施策略.图1为5 dB雷达回波信号的奇异值和差分谱,由图1b)可知,第二个差分谱最大,若是将其后的奇异值置零重构,必然会导致信号大量失真,为了在剔除复杂干扰的同时尽可能减少有用细节的流失,以奇异值的差分谱作为进行2级奇异值分解的标准,将最大差分谱(图1b)箭头所指)所对应的奇异值作为临界值,前面较大大的奇异值重构后记为B1,后面较小的奇异值重构后记为S1,然后对S1进行下一级分解.2级奇异值分解后信号的奇异值和差分谱见图2,由图2a)可知,表示信号的较大奇异值已经变少,根据最大差分谱区分原则,将前面较大大的奇异值重构后记为B2,后面较小的奇异值重构后记为S2.3级奇异值分解后信号的奇异值和差分谱见图3,3级分解后奇异值虽然呈递减分布,但是从图3b)可知,其差分谱相差较小,分布比较均匀,说明信号中的主要成分为噪声信号,则分解停止,多级奇异值分解处理后的信号就记为B1+B2,通过多级奇异值分解的实施策略可以得出如下结论:原始信号信噪比越低,多级奇异值分解的次数越多.图4为降噪前后雷达回波信号时域波形图,图5为降噪后信号和干净信号的相对误差,可以看出,信号特征基本被还原,但信号略显粗糙,存在毛刺和尖锐,说明,对于较低信噪比信号降噪问题,单一的信号处理方法很难取得理想效果. 图1 SNR=5 dB雷达信号的奇异值和差分谱 图2 2级分解后的奇异值和差分谱 图3 3级分解后的奇异值和差分谱 图4 降噪前后雷达信号时域图 图5 降噪后雷达信号相对误差 经多级奇异值分解处理后的信号虽然有用信号占绝大比重,但是还有少许噪声干扰,信号还存在毛刺和尖锐.SG滤波算法是一种移动窗口的加权平均算法,通过最小二乘法求取多项式系数,得出滑动窗口中心点的最佳拟合值.利用SG对多级奇异值处理后的信号进行平滑修正处理,可进一步提高信号信噪比[15]. 对于含噪序列点{x1,x2,…,xN},假设拟合曲线方程为 地表水受到严重污染,城镇供水水源地水质不能达到有关标准;大量未经处理的废污水排入河道和渗井、渗坑,加之过量使用农药和化肥,使得河流和地下水受到严重污染。城市下游河道多为不能利用的超V类水体,减少了水资源的可利用量。 x(t)=a0+a1t+a2t2+…+antn,n∈Z (4) 式中:n为拟合阶数. 最小二乘算法的拟合残差为 (5) 式中:x(t)为拟合点;xt为实际数据点;2M+1为数据窗口,t=-M为数据窗口最左边的数据点;t=M为数据窗口最右边的数据点. 若系数ai(i=0,1,2,…,n)满足式(8)最小,则认为点为序列的最佳拟合点.由微积分知识可知,若εN最小,则其对各个参数的导数应该为零,于是 (6) 为了计算方便,引入一个2M+1行n+1列的辅助矩阵A,设A={at,i}.其中,at,i=ti,-M≤t≤M,0≤i≤n. 设辅助矩阵B,使B=ATA. (7) 设 于是 Ba=ATAa=ATx a=(ATA)-1ATx=Hx (8) 将多项式系数矩阵a代入到式(7)中就可以得到SG平滑滤波后信号. 综上所述,多级奇异值分解和SG降噪方法的实施流程见图6. 图6 多级奇异值分解和SG降噪方法流程图 为了验证所提方法的有效性和对雷达信号处理的优势,以Matlab仿真的“chirp”信号为例,与文献[14]方法作对比分析,其中采样频率为1 kHz,采样时间为0.5 s.图7~8为文献[14]和本文方法的降噪效果图,由图7~8可知,文献[14]降噪方法对重构阶次的选取方法加以改进,但是无法更加细化地提取淹没在噪声主导奇异值中的有用细节,降噪后信号明显粗糙(如图中箭头所示),降噪后信号和干净信号的相对误差较多级奇异值分解处理后信号要大(见图5),而本文方法处理后的信号基本已无明显毛刺,信号比较光滑,并且和干净信号相对误差最小,说明了SG平滑滤波算法进一步修正了信号轨迹,平滑掉了残留噪声. 图7 文献[14]降噪效果图 图8 本文方法降噪效果图 对于已知模型产生的信号,可以采用信噪比(SNR)和均方误差(MSE)定量衡量降噪效果,信噪比越大,均方误差越小,降噪效果越好[16].表1为不同信噪比原始信号的降噪效果对比,由表1可知,对于不同信噪比的雷达回波信号,本文方法都有着较好的降噪效果,并且原始信号信噪比越低,降噪效果优势越大,体现了所提方法对于处理较低信噪比雷达信号的优越性,更加适用于复杂环境下雷达信号处理,应用前景更广. 表1 降噪效果比较 将本文提出的降噪方法应用于雷达信号的降噪,带宽为30 M,脉宽为10 μs,采样频率为150 MHz,取11 000~14 000为样本点数,其实测波形图见图9,受到复杂噪声干扰,从时域图中很难准确提取信号特征. 图9 实测雷达信号 图10~11为文献[14]和本文方法的降噪效果图.文献[14]降噪后的波形图局部毛刺明显,波形不够光滑,而本文所提方法去噪后的信号整体比较平滑,无明显毛刺,效果要优于文献[14]降噪方法. 图10 文献[14]降噪效果图 图11 本文方法降噪效果图 考虑到实验信号先验知识未知,不能采用信噪比和均方误差来定量比较两种方法的降噪效果,根据信号都有一定的相关性,而噪声不相关特性,因此,信号的自相关函数要远远大于噪声.自相关函数定义为 式中:τ为延迟;N为信号长度. 2种方法去噪前后的部分自相关函数值见图12,由图12可知,本文所提方法降噪后序列的自相关函数值要明显大于文献[14],说明原始信号经本文方法降噪后信号比重要大于文献[14],进一步展现了其降噪的优越性. 图12 两种方法自相关函数 针对雷达信号降噪问题,提出了基于多级奇异值分解和SG的降噪方法,详述了多级奇异值分解的实施策略,克服了奇异值分解重构阶次难以有效选取的难题,以先验知识已知和先验知识未知的雷达信号为例,进行了仿真和实验对比分析,结果表明,含噪信号经多级奇异值分解处理后,再经SG平滑滤波,有效剔除复杂干扰,减少有用信号失真,真正实现了降噪目的.对于有无先验知识的雷达信号,所提方法也有较好的降噪效果.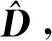
1.2 多级奇异值分解实施策略

2 SG滤波算法
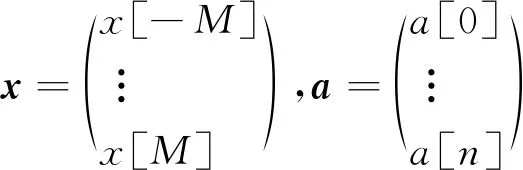
3 仿真分析
4 实验分析
5 结 束 语
