“数学抽象”不抽象

王士勇

数学抽象是指通过对数量关系与空间形式的抽象，舍去事物的一切物理属性，得到研究对象的素养.主要包括从数量与数量关系、图形与图形关系中抽象出数学概念及概念之间的关系，从事物的具体背景中抽象出一般规律和结构，并用数学语言予以表征.可以说，数学抽象不仅是一种素养，也是一种思维过程.接下来，笔者结合具体案例，运用“三步抽象”（条件的抽象、问题的抽象和数学的表征）对学科间问题向数学问题的有效转化进行说明.

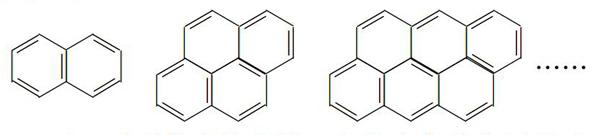
案例1沥青中存在着一系列稠环芳烃，它们彼此虽然不是同系物，但其組成和结构都是有规律变化的：

……

这一系列化合物中第n个化合物的分子通式可以表示为_____（用n表示）.

条件的抽象：将一系列稠环芳烃结构简式抽象成一一对应的碳原子数的一列数和氢原子数的一列数.

问题的表述：从两列数中寻找出通式中碳原子数和氢原子数的规律性，即求通式抽象成求数列的通项公式.

数学的表征：求数列10，16，22，……和数列8，10，12，……的通项公式.

经过三步抽象后，学生很容易求得碳原子数和氢原子数的通项公式分别为6n+4、2n+6，所以这一系列化合物中第n个化合物的分子通式为C6n+4H2n+6（n∈N）.

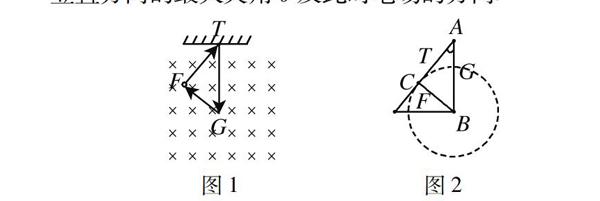
案例2用绝缘细线悬挂一质量为m，带电量为+q的小球，竖直平面内有场强为E、方向不定的匀强电场，且qE

条件的抽象：将重力抽象成长度为G的定线段AB.将电场力抽象成长度为F的线段BC，其中点C轨迹是以B为圆心，F为半径的圆.将拉力T抽象成线段AC，其长度、与AB的夹角均不确定.