化归思想在高中数学中的应用策略
2020-08-25汤晓玲
汤晓玲
(江苏省海门中学 226100)
化归是一种数学思想,也是解决数学问题的基本方法之一.化归思想,体现了学生对数学知识向能力转换的重要手段,对于促进学生加深对数学知识的理解和应用意义重大.如函数中变量的运动变化,概率中的现象与本质等数学问题,都用到化归思想.现结合高中数学,就化归思想的运用策略进行阐述.
一、化归思想,为探究函数问题提供教学指引
在数学领域,对一些运动变化现象的表达,多利用化归思想.如三角函数中循环往复的规律,可以从角度量向弧度量的转化,从而在角度与实数之间形成对应关系.同样,利用单位圆与有向线段,可以实现角度与坐标系之间的关联,实现数形结合.与此相关的,对三角函数知识的延伸,有弦与切互化,积化和差、和差化积,以及半角公式、倍角公式等变换等等,都是化归思想的典型运用.高中数学中,初等函数知识的学习,引入导数来探讨函数的单调性、极值、最值问题,可以实现对高次方程、不等式,转换为简单的数学问题.
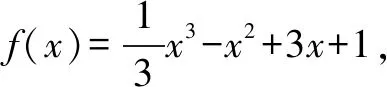
由此可知,对于化归思想的运用,在分析函数问题时,要把握特殊点的转换,灵活运用多种转化策略,如拼凑法、换元法、构造法等等.面对数学问题,教师要引领学生探索数学知识的解题路径,找准突破口,特别是结合题设条件,引入等价转化,变抽象性数学问题为直观性、简单性问题,从而梳理出解题思路.解决数学问题的方法很多,但不同的解题技巧,需要学生充分运用数学思想,来寻找更佳的化归路径.函数问题多样、复杂,对化归思想的运用,有助于拓展学生的解题视野,将a问题转化为b问题,以学生熟悉的解题方式来求解,提高解题效率.
二、化归思想,在几何代数中展现演绎推理
几何学中的演绎推理是重要的解法思路,也是应用化归思想的典型.无论是立体几何,还是解析几何,化归思想应用广泛.分析立体几何中点、线、面的关系,可以通过化归将几何问题转化为代数问题.同样,对于面面平行、面面垂直问题,也可以利用化归思想,实现线面平行、线面垂直等相互转化.解析几何,往往从数形结合思路,通过化归,将图形问题与代数问题建立关联.如在分析一些解析几何题目时,引入坐标系媒介手段,利用代数反演方法来解决解析几何问题.比如对于二元一次方程组,其解与坐标系中的交点问题具有关联性;对于圆锥曲线与二元二次方程,普通方程与极坐标方程等,都可以从化归思想中实现问题转化.
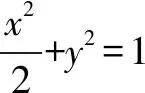
分析解析几何中的最值问题,往往需要从数学逻辑推理中,引入化归思想,将抽象的数学问题,转化为具象问题,以代数方法来进行运算,抓住解题的关键点,实现以简驭繁.化归思想的特征,在于实现逻辑推理,可以从一般到特殊,还可以从特殊到一般,完成对问题的简化处理.如等差数列中的累加法、等比数列中的累乘法,数列求和中的裂项相消法、错位相减法等等,这些都是化归思想的具体应用,都在于利用代数手段来找到求解问题的方法.
三、化归思想,从概率统计中化隐为显
在认识自然、改造自然过程中,对天文地理等知识的研究,从中归纳出概率、统计的基本理论.对于概率,可以解释为对一种随机现象的统计与预测.

概率类数学题目,主要是运用统计分析方法,对可能的随机现象发生可能性的预测.面对该类题型,往往需要将真实问题转换为数学统计问题.教师在剖析概率、统计题意时,可以通过游戏法、试验法、观察法等,对发生的可能性进行估算.
四、化归思想,从建模中解决数学问题
数学问题与现实生活关系紧密,在解决数学问题时,教师要积极通过化归思想,完成对数学问题的建模探究.等价性变换是化归思想的典型应用,借助于数学知识,对数学形式进行变换,引领学生利用数学符号来表征数学问题,发展学生数学思维.数学建模探究,就是要引领学生从数学问题中提炼建模的方法,将数学情境转化为数学问题,通过数学模型来回归现实,回归数学的本质.某题中,有本金50万,有三种投资方式.第一种投资理财产品,每日获利50元;第二种投资理财产品,第一天获利5元,以后每天比前一天多15元;第三种理财产品,第一天获利0.4元,以后每天是前一天的2倍.请同学结合不同的理财产品,分析和计算出最佳的理财方案.针对该题的分析,先要对不同投资方案进行数学模型构建.第一种,可以构建为常函数模型,y=50,x∈N;第二种,可以构建为一次函数模型,y=15x-10,x∈N;第三种,可以构建为指数函数模型,y=0.4×2x-1,x∈N.由此,根据投资的天数为正整数,可以根据不同的数学模型,分别对其不同天数的获利值进行计算与对比.发现,当天数低于6时,购买第一种方案利润更高;当天数6
总之,化归思想体现了对复杂问题的简洁化转换,高中阶段在数学解题中,要指导学生利用化归思想,把握化归思想的特点,灵活选择解题方向,帮助学生提高解题质量和效率.
