基于MATLAB的倒立摆模糊自适应PID控制研究

王立红，谢忠刚，王玉莹

(1.辽宁工业大学 电气工程学院，辽宁 锦州 121001；2.鞍钢集团矿业弓长岭有限公司 选矿分公司，辽宁 辽阳 111008；3.鞍钢集团矿业有限公司 教育培训中心，辽宁 鞍山 114000)

0 引言

PID控制是古典控制理论中被广泛采用的控制规律，主要应用于各种线性系统，它的控制精度由被控对象的模型精度决定[1]。在倒立摆系统中，存在一定的非线性和不确定性等因素，导致传统的控制方法具有一定的局限性。模糊控制是一种采用语言控制规则的方法，不需要建立被控对象精确的数学模型，凭借现场操作人员的经验或相关专家的知识，使得设计更加简单[2]。本文将传统PID控制和模糊控制相结合，根据PID控制器的三个参数(比例系数KP、积分系数KI、微分系数KD)与偏差e和偏差变化率ec之间的模糊关系，在运行过程中不断修改KP、KI、KD，让PID参数具有自适应能力，构成模糊自适应PID控制器，并利用MATLAB进行仿真，仿真结果表明本文采用的方法能有效控制摆杆的角度。

1 一级倒立摆的数学模型

1.1 一级倒立摆控制原理

图1为直线一级倒立摆工作原理框图。数据采集卡将采集到的旋转编码器的数据传送给计算机，并与设定值进行比较，将偏差经过某种运算之后发出控制规律，控制电机使摆杆左右摆动进入稳摆范围，从而实现摆杆直立不倒以及自摆起。

图1 直线一级倒立摆工作原理框图

1.2 倒立摆的传递函数

在忽略空气阻力和各种摩擦的条件下，直线一级倒立摆可以看作是由小车和匀质杆组成的系统[3]。现做如下假设：小车质量为M，摆杆质量为m，小车与接触面的摩擦因数为f，摆杆转动轴心到杆质心的长度为l，摆杆的转动惯量为I，施加在小车上的作用力为F，小车位移为x，摆杆与垂直向上方向的夹角为Φ，摆杆与垂直向下方向的夹角为θ。采用牛顿-欧拉法建立倒立摆数学模型的过程如下：

(1)

(2)

对于质量均匀分布的摆杆，系统的传递函数为：

(3)

其中：g为重力加速度。

2 模糊PID控制器设计

模糊控制器采用二维模糊控制器，输入变量为误差e和误差变化率ec，经模糊化后变成模糊量E和EC，经过模糊推理和模糊决策后得到模糊输出量U，再经过清晰化后得到精确的输出量u，也就是PID控制器的参数KP、KI、KD。模糊自适应PID控制原理如图2所示。其中，r为输入，y为输出，αe、αc分别为误差、误差变化率的量化因子，αu为输出量的比例因子。一般情况下，αe越大，系统的超调量越大，过渡过程就越长，反之，系统变化越慢，稳态精度降低；αc越大，系统输出变化率越小，系统变化越慢，αc越小，系统反应越快，但超调量增大；αu越小，系统过渡过程越长，αu过大，会导致系统振荡。

If E=PB and EC=NB then U=ZO

If E=PB and EC=NM then U=NS

If E=PB and EC=NS then U=NS

If E=PB and EC=ZO then U=NM

If E=PB and EC=PS then U=NM

If E=PB and EC=PM then U=NB

If E=PB and EC=PB then U=NB

由此可以建立完整的模糊控制规则表，本文不再详述。

图2 模糊自适应PID控制原理图

3 仿真分析

本实验一级倒立摆的物理参数如下：小车质量M=0.618 kg，摆杆质量m=0.073 7 kg，摆杆长度L=350 mm，摆杆质心到转轴的距离l=122.5 mm。将数值代入公式(3)中得到此时的传递函数为：

采用PID控制，建立系统的仿真模型，如图3所示。在5 s时加入阶跃扰动，仿真波形如图4所示。

图3 PID控制仿真模型

由图4可以看出：采用PID控制，系统的输出会产生较大的超调，受扰动后输出波动较大，但最后能够恢复到稳态无静差。

建立模糊自适应PID控制器仿真模型,如图5所示，在5 s时加入阶跃扰动，仿真波形如图6所示。

由图6可以看出：采用模糊PID控制后，系统的输出曲线变得光滑，超调量明显减小，受扰动后输出波动变化不大，系统性能有所提高。

4 结论

本文将模糊控制和传统的PID控制相结合，设计了模糊自适应PID控制器，作为一级倒立摆的控制器；根据摆杆角度与竖直方向的偏差和偏差变化率，通过模糊推理，在线修改PID控制器的参数KP、KI、KD。仿真结果表明：模糊PID控制能有效改善系统的动态性能，同时提高系统的抗扰性。

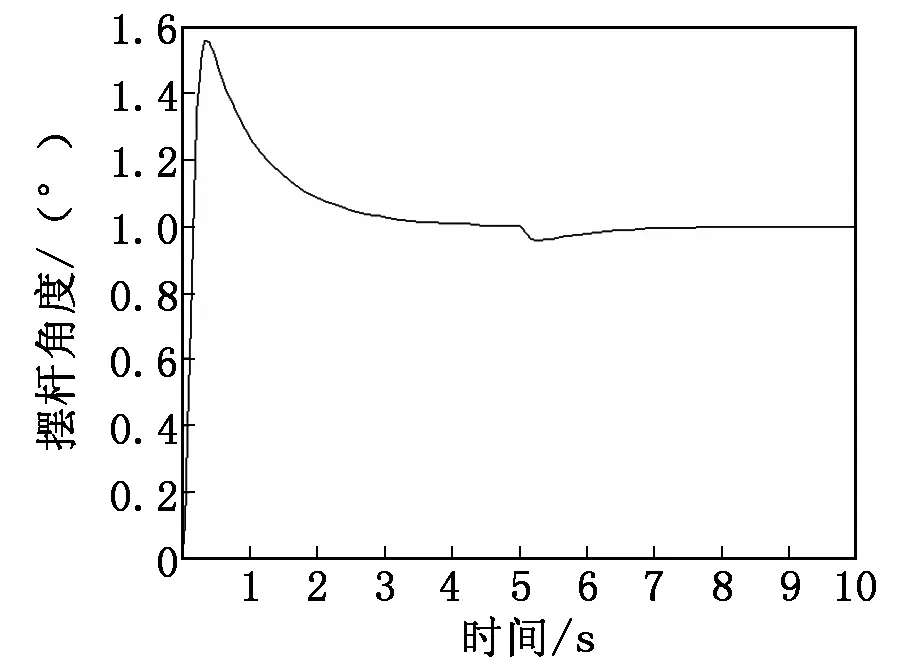
图4 PID控制摆杆角度曲线

图5 模糊自适应PID控制器仿真模型

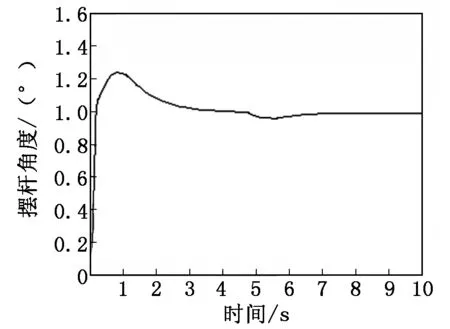
图6 模糊自适应PID控制摆杆角度曲线