管道清淤机器人悬架机构越障性能优化与仿真

韩梦泽，郭京波，张 潮

(石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室，河北 石家庄 050043)

0 引言

随着机器人技术的快速发展，国内外排水管道检查、清淤工作不断由管道机器人代替[1]。针对管道内的复杂环境，管道机器人必须具有良好的行驶性能，尤其是较强的越障能力，因此对管道机器人的越障性能研究一直是机器人研究领域的热点之一[2]。文献[3-4]建立了机器人越障过程中的动力学模型，研究了一些运动学限制条件对机器人越障性能的影响。文献[5]提出了一种基于遗传算法的质量选择的优化模型，并基于ADAMS仿真验证了该方法的正确性。但现有文献关于管道机器人移动机构对越障性能影响的研究较少。本文针对设计的一种悬架式管道清淤机器人，以悬架越障时的准静力学模型为基础，利用控制变量法和序列二次规划法对悬架尺寸进行优化，以降低越障时电机的能耗。

1 悬架越障通过条件

管道清淤机器人通过悬架完成越障，为确保悬架参数基于同一障碍优化，需要分析悬架越障的通过条件。垂直障碍是常用于评定管道机器人越障性能的重要指标，结合管道内常存在碎石块等建筑垃圾的实际情况，采用阶梯障碍类型。在分析时假设：①悬架为刚性，且结构对称；②车轮为刚性；③悬架质量忽略不计。

管道清淤机器人前轮越障时的受力情况如图1所示。图1中，N1、N2、N3分别为地面作用在前、中、后轮的支撑力，Ft1、Ft2、Ft3分别为前、中、后轮的水平驱动力，Gr为车轮重量，Gb为一半车体重量，C为车体的质心点，P2为摆杆与摇臂的铰接点，P1为悬架与车体的铰接点，O、P3、P4分别为前、中、后轮与悬架的铰接点；h为障碍高度，α为支撑力N1与水平线的夹角，lp、l2、l3、lb分别为铰接点P2、P3、O和质心点C到铰接点P4的水平距离，hp为铰接点O到铰接点P2的垂直距离，r为车轮半径。

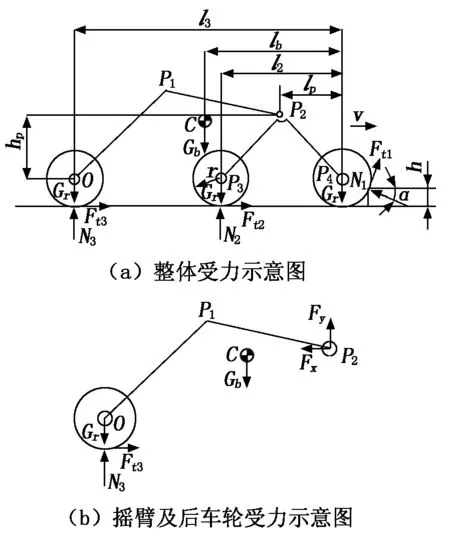
图1 管道清淤机器人前轮越障时准静力学模型

以水平方向为X轴、垂直方向为Y轴，通过静力学分析可得平衡方程组：

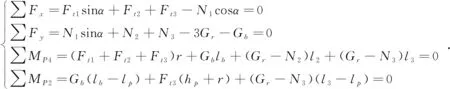
(1)

且

Fti=φNii=1,2,3.

(2)

其中：φ为附着系数。

由图1几何关系可知：

(3)

将式(1)～式(3)联立得：

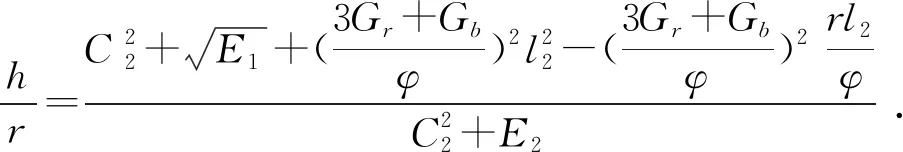
(4)

其中：

(5)

(6)

(7)

(8)

同理可得中轮和后轮的越障通过条件，此处不再赘述。通过分析可知在管道清淤机器人的结构参数不变和附着系数相同的条件下，前轮可越障高度最小。

2 悬架结构优化

2.1 设计变量

取单侧悬架进行研究，以后轮与摇臂的铰接点为原点O，机器人移动方向为x正轴建立坐标系，如图2所示。图2中，P1、P2、P3、P4为悬架铰接点，其坐标初值为：D1=180 mm，D2=200 mm，D3=300 mm，D4=150 mm，D5=180 mm，D6=430 mm。

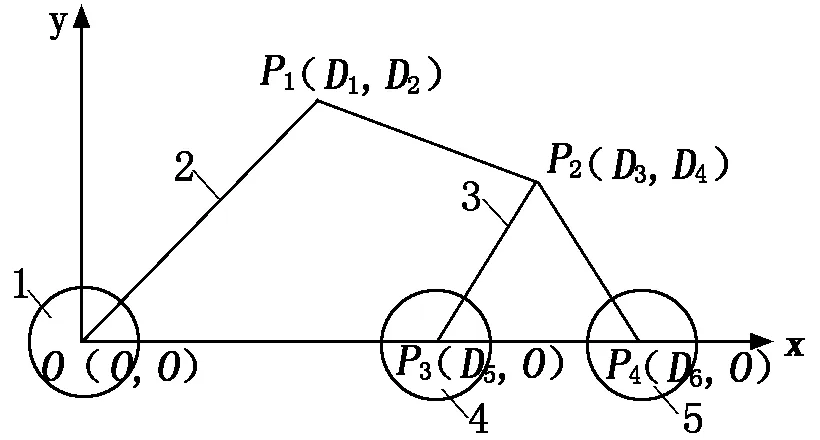
1-后轮；2-摇臂；3-摆杆；4-中轮；5-前轮

车轮半径为给定值，质心位置由悬架与车体铰接位置决定。其余的6个参数作为设计变量,记为：

D=[D1,D2,D3,D4,D5,D6]T.

2.2 约束条件

为防止管道清淤机器人通过障碍时发生干涉，要求其具有几何通过性[6]，悬架与车体的铰接点P1高度大于最小离地间隙；在前轮爬上障碍后，中轮在越障时避免障碍与摆杆发生干涉。约束条件如下：

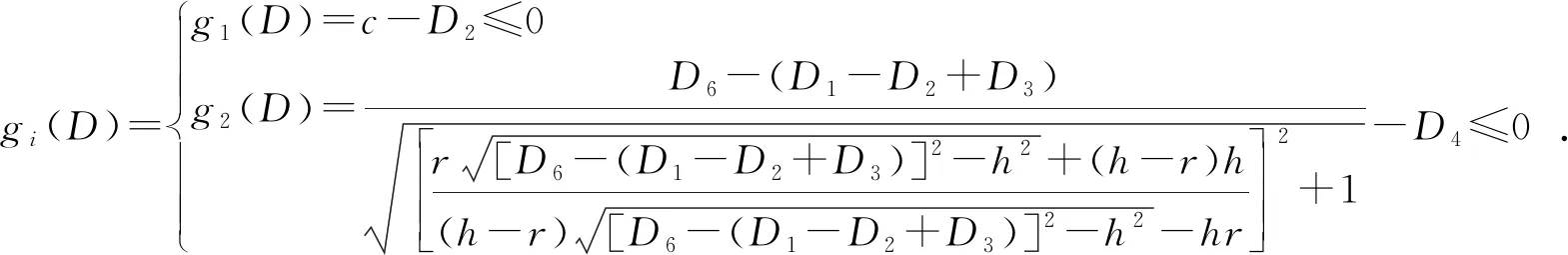
(9)

式中：c为最小离地间隙；h为最大障碍高度。

2.3 目标函数

悬架越障的过程包括前轮、中轮、后轮越障三个阶段。以机器人完整越障所需的电机能耗大小来表示悬架的越障能力，消耗的总功值越小，说明当前尺寸下的悬架越障能力越强。目标函数表示为：

U(D)=W1+W2+W3.

(10)

其中：W1、W2、W3分别为前、中、后轮驱动电机消耗的能量；U为总功耗。

2.4 单设计变量研究

利用控制变量法，逐个分析变量对目标函数的影响大小。由于ADAMS软件可以直接测量输出功率，所以用输出功率间接表示电机消耗的总功。

取φ=0.7，r=75 mm，Gr=1.1 kg，Gb=15 kg，将设计变量初值代入式(4)得障碍极限高度为90.3 mm，考虑误差因素，建立高75 mm障碍和悬架模型导入ADAMS进行越障仿真。将设计变量按照表1中取值范围进行赋值，得到该变量取不同值的功率变化曲线。图3为变量D1取不同值时的功率曲线，其他变量同理可得。

表1 设计变量取值范围

由于功率变化曲线不能较为直观地表明各设计变量对目标函数的影响大小，对各变量功率曲线进行定积分计算，便得到完成一次越障悬架所消耗的功，表2为D1变量定积分计算结果即D1对目标函数的影响，其他变量同理可得。通过分析可知，设计变量D3、D4、D5对目标函数影响较大，D1、D2、D6各自取值为195 mm、185 mm、415 mm时越障能耗最小。

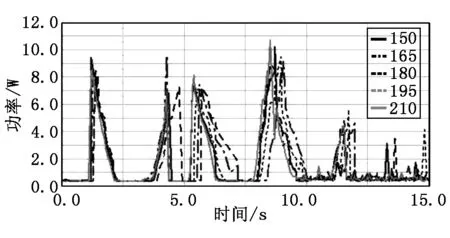
图3 D1取不同值时的功率变化曲线

表2 D1对目标函数的影响

2.5 多设计变量研究

以悬架越障能耗最小为最优目标函数，由式(9)、式(10)以及上节内容得：

(11)

序列二次规划法是求解该式的最有效方法。建立式(11)相对应的拉格朗日函数：

L(D,λ)=U(D)+λTg(D).

(12)

其中：λ为拉格朗日乘子向量。

将拉格朗日函数L(D,λ)和约束函数g(D)在给定点Dk做泰勒展开，分别取到二次项和线性项：

L(Dk+1,λk+1)=L(Dk,λk)+[L(DK,λK)]T(Dk+1-DK)+

(13)

其中：Hk为Hesse矩阵。

g(Dk+1)=g(Dk)+[g(Dk)]T(Dk+1-Dk).

(14)

对式(12)在给定点Dk进行一阶求导：

L(Dk,λk)=U(Dk)+[g(Dk)]Tλk.

(15)

设

(16)

将式(15)、式(16)代入式(13)中，得：

L(Dk+1,λk+1)=U(Dk)+(λk)Tg(Dk)+g(Dk)dk+

(17)

将式(16)代入式(14)中，得：

g(Dk+1)=g(Dk)+[g(Dk)]Tdk.

(18)

便将非线性规划问题转换为序列二次型规划问题：

(19)

其中：QP(d)为关于d的二次规划法函数。对式(19)进行求解得到dk，然后确定步长μk，按照Dk+1=Dk+μkdk进行迭代，得到目标的最优解。

使用ADAMS/View中优化分析工具箱通过迭代运算寻找到设计变量的最优解，计算结果如图4所示。

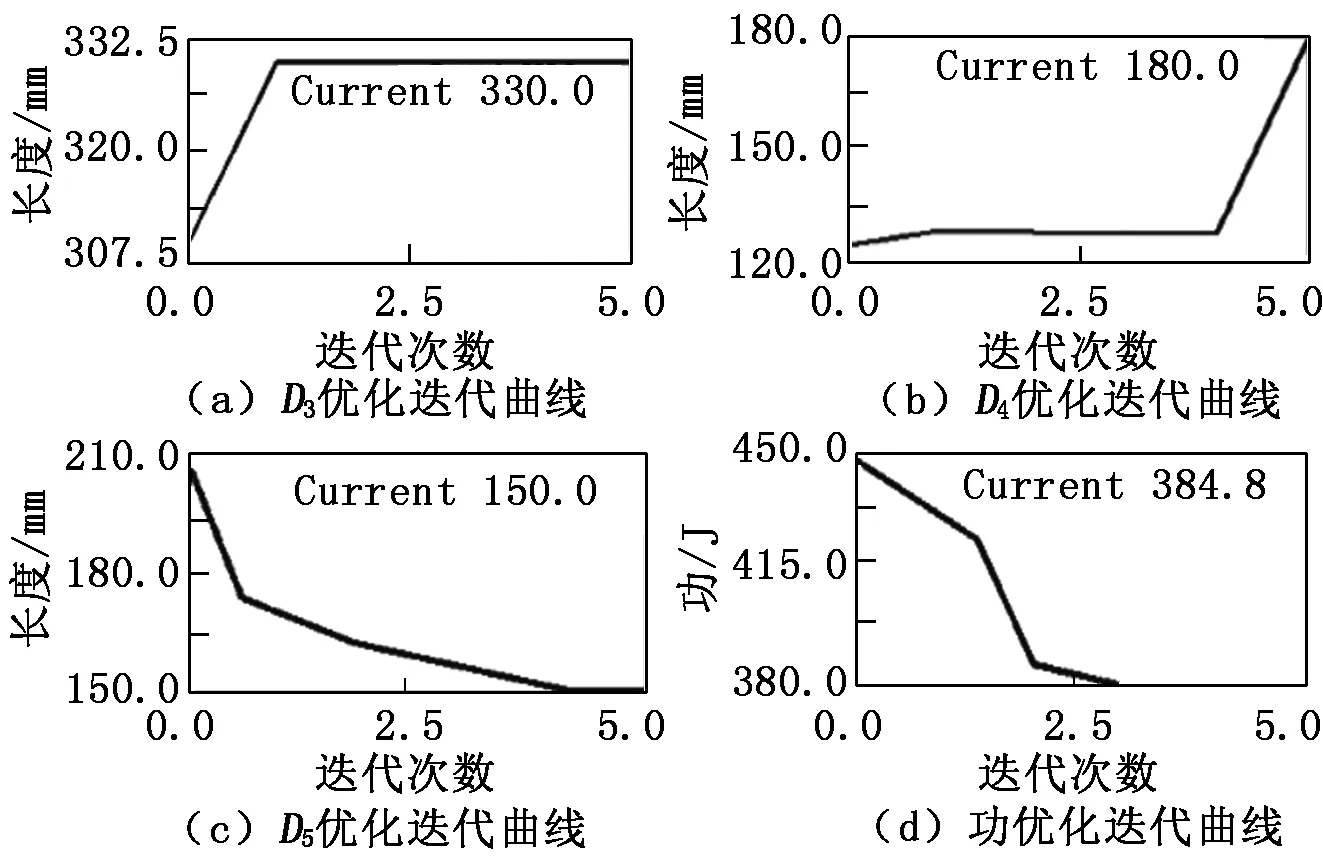
图4 设计变量及总功耗的优化迭代变化曲线

由图4可知：D3、D4、D5的最优解分别为330 mm、180 mm、150 mm；优化前后能耗分别为440.7 J与

384.8 J，即通过优化能耗降低了12.7%。

3 管道清淤机器人动力学仿真

在ADAMS/View建立管道清淤机器人虚拟样机，内径为1 000 mm的管道以及高度分别为50 mm、100 mm以及150 mm的障碍模型。

运行三组仿真，机器人均可成功越障，验证了优化结果的正确性。机器人在越障过程中的速度曲线如图5所示。以150 mm越障速度曲线为分析对象，从图5中可看出，0 s～10 s为前轮越障阶段，用时10 s，10 s～16 s为中轮越障阶段，用时6 s，16 s～26 s为后轮越障阶段，用时10 s；并且前轮越障时在速度为零的时间最久，这与准静力模型分析相符。

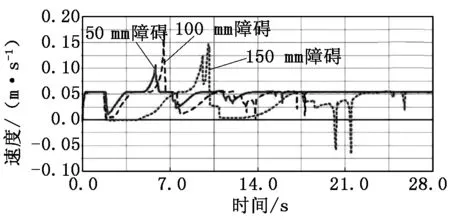
图5 管道清淤机器人越障速度曲线

4 结论

结合管道清淤机器人悬架的基本结构，建立了越障时的准静力学模型，分析得出机器人可越垂直障碍的最大高度。在此基础上构建了优化数学模型，利用控制变量法和序列二次规划法对悬架尺寸进行优化，得到了最优尺寸。通过ADAMS的仿真，结果显示该尺寸下的悬架越障时电机能耗得到明显降低，并验证了优化结果的正确性，为管道清淤机器人悬架参数优化设计提供了可行的方法。