针对多工况覆晶旋转轴共振的改进型滤波器设计
2020-08-25廖俊鸿贺云波王忠诚黎炜天
廖俊鸿,贺云波,王忠诚,黎炜天
(广东工业大学 机电工程学院,广东 广州 510006)
0 引言
回顾2019年国内半导体装备行业,中国本土的半导体设备需求大增,设备产业的发展呈现越来越重视下游封装设备的趋势。相较于传统的引线键合技术,倒装焊封装技术由于把芯片通过焊球直接连接在基板上,使得单位面积内I/O数量更多、散热性更好以及可靠性更高[1]。本文研究的轨道式倒装装备是一款在半导体封装中起关键作用的先进封装设备,其覆晶旋转轴正是执行一系列取晶、覆晶动作的核心作用轴。
由于覆晶旋转轴存在不同情况下的共振模态,包括高增益状态下振动模态易被激发、振动模式的耦合以及多工况下共振模态参数摄动范围大等问题,影响到其正常的工艺流程。因此,本文首先进行覆晶旋转轴不同工况的共振模态分析,然后进行辨识实验获取共振特性数据,最后针对性地提出一种改进型的陷波滤波器设计方法,并对其进行验证。
1 覆晶旋转臂的共振模态分析
在对轨道式倒装机进行实际调试时发现,覆晶旋转轴存在若干情况下的共振现象,均对取晶和覆晶的芯片转移过程产生影响,严重时覆晶旋转轴甚至直接掉电。针对具体问题的分析如下:
1.1 高增益状态下振动模态易被激发
覆晶旋转轴是直接驱动轴,其直接连接到动负载上以实现驱动力与负载的刚性耦合,但是由于覆晶旋转轴和支撑件等连接件之间的柔性环节会降低系统刚度,继而容易激发共振现象。电机调试中,为提高系统的闭环频宽,需要在一定范围内提高控制器的比例增益,以提高快速响应能力,降低位置跟踪误差,从而提高控制性能。但是,控制器的比例增益越高,系统响应越大,有可能导致系统震荡甚至掉电。这说明了系统潜在的振动模态会被稍高的控制器比例增益所激发出来。本文以本单位自行研发的轨道式倒装机的覆晶旋转轴作为研究对象,控制器增益通过调用GHN系列运动控制卡的功能函数输入,并通过增量式光栅尺采集反馈位置信息,最后用MATLAB绘制出不同增益下的调试效果,如图1所示。由图1可知:控制器增益越高,系统响应越大,振动模态越容易被激发。

图1 覆晶旋转轴在不同增益下的振动模态(伯德图)
1.2 振动模式的耦合问题
在对覆晶旋转臂的调试过程中,发现系统存在振动模式的耦合问题。覆晶旋转臂除了自身是直驱运动轴之外,另一层面上也是覆晶模块Z轴的负载。分别对两者进行扫频实验以获取频域数据,得到覆晶Z轴和覆晶旋转轴的速度闭环扫频结果,如图2所示。由图2可知:Z轴和旋转轴在170 Hz的频率点上均有较大的幅值响应值。未针对Z轴在170 Hz频率加滤波器前,发现Z轴和旋转轴在运动过程均产生振动,其中Z轴振动程度相对激烈,但振动频率均在170 Hz频率处。当针对Z轴用陷波滤波器过滤170 Hz共振频率点后,发现Z轴和旋转轴的振动现象消失,这说明覆晶旋转轴受到Z轴的振动影响。
综上分析,覆晶臂模块存在振动模式的耦合问题:在Z轴上的振动输入,导致了另一旋转轴上的振动响应。
2 多工况下覆晶旋转轴共振特性的获取
上一节中,已对覆晶旋转轴不同情况下的共振模态进行了分析。接下来将进行正弦扫频实验以得到覆晶旋转轴系统的输入输出数据;然后对数据进行快速傅里叶变换,获得系统的共振特性。
在对覆晶臂两轴进行正弦扫频实验时,发现旋转轴置于不同位置时,获得的扫频结果存在明显的差异性,即部分频率点上的幅值和相位角大小不一致或发生偏移。如果排除外界的干扰,分析认为覆晶旋转轴处于不同位置时,系统刚度出现不同程度改变,导致相同被控对象不同位置的开环扫频结果有差异性。因此,为保证数据的严谨性和准确度,在对覆晶旋转轴进行正弦扫频实验时,分别采集其处于三个特定位置时的开环扫频数据。覆晶旋转轴处于不同位置时的状态图如图3所示。
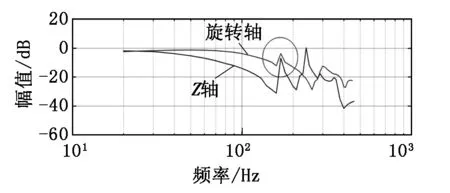
图2 覆晶Z轴和覆晶旋转轴的速度闭环扫频结果(伯德图)
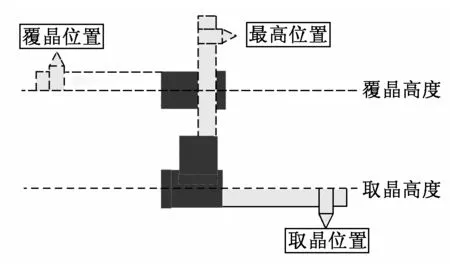
图3 覆晶旋转轴的不同位置状态
正弦扫频实验是通过向覆晶旋转臂系统输入一系列不同频率的正弦激励信号,再通过其反馈装置采集相应的位置输出信号,从而获得覆晶旋转臂系统的输入输出数据集。实验的设置参数如下:正弦激励信号的起始频率为10 Hz,结束频率为2 000 Hz,步长为5 Hz,增益为200,持续时间为1 000 ms。通过实验及数据后处理,得到当覆晶旋转轴分别处于取晶位置、覆晶位置和最高位置的情况下覆晶旋转轴的频域特性,如图4所示。

图4 不同位置覆晶旋转轴的频域特性(伯德图)
3 改进型陷波滤波器的设计和实现
第1节中所讨论的共振模态问题存在的根本原因是覆晶旋转轴系统的某些环节刚性不够,存在若干谐振频率点,引起系统共振[2]。有效的解决办法是获取系统的谐振频率点,并降低该频率点的响应幅值。本文采用一种改进型陷波滤波器(notch-filter)的方法来解决该问题,并分析其数字离散化的实现过程,最后进行陷波滤波器对覆晶臂旋转轴的振动抑制实验,检验滤波效果。
典型的二阶结构陷波滤波器的传递函数表示为[3]:
(1)
其中:ωn为陷波滤波器的作用中心频率;ξ为阻尼比。
取谐振频率ωn=1 000 rad/s,分别取ξ的值为0.5、5和50,使用MATLAB绘制陷波滤波器的幅频响应和相频响应曲线,如图5所示。从图5中可以看出:ξ值越小,谐振点的响应幅值越小,即对谐振频率点的抑制效果越强,但同时影响谐振点附近范围的频率信号。因此,单一变量ξ的取值既影响陷波深度,又影响陷波宽度,无法达到可调节性高、减少对有用信号负面影响的滤波效果,而且如果给系统施加不当的过滤效果,有可能破坏系统稳定性。

图5 不同ξ值下传统陷波滤波器的伯德图
针对上述传统陷波滤波器的单一参数调节问题,在原函数基础上引入一个可调变量,得到改进型的陷波滤波器,其传递函数表示为:
(2)
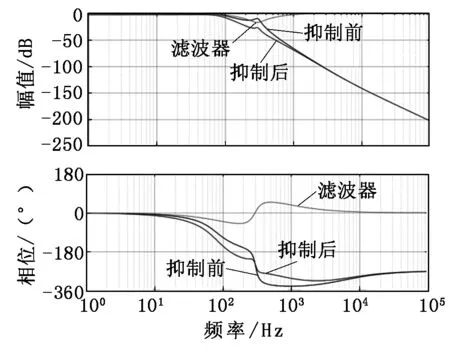
其中:j为陷波深度系数;k为陷波宽度系数。由于陷波深度系数j和陷波宽度系数k之间的关系满足条件0 为了单独讨论陷波深度系数j和陷波宽度系数k各自对过滤效果的影响,进行两组实验:第一组实验中,保持ωn=1 000 rad/s、陷波深度系数j=0.5不变,分别取k值为2、20和200的不同情况,并获取其所对应的滤波器幅相频特性曲线,如图6所示;第二组实验中,保持ωn=1 000 rad/s、陷波宽度系数k=20不变,分别取j值为0.02、0.2和2的不同情况,并获取对应的滤波器幅相频特性曲线,如图7所示。 图6 不同k值对陷波滤波器的影响 从图6可以看出:满足0 从图7可以看出:满足0 图7 不同j值对陷波滤波器的影响 改进型陷波滤波器的设计仅是模拟陷波器的理论设计,在离散系统中数字化实现,通常使用一个差分方程表示[4]: (3) 其中:N为差分方程的阶数;ai、bi均为滤波器系数;x(n)为输入信号值;y(n)为输出信号值;n为整数。差分方程求解的关键是确定滤波器系数ai和bi。 双线性变换法本质上是通过一阶估计法实现从连续时域到离散时域的传递函数变换,其从s平面到z平面的映射关系为: (4) 其中:T为采样间距。 由式(2)可知,设计好的模拟陷波滤波器的传递函数为: (5) 根据s平面到z平面的映射关系,将式(4)代入式(5)可得: (6) 通常,分母的常数项被标准化为1,于是有: (7) 其中: (8) 由于 (9) 对式(7)推导得到相应的差分方程: y(n)=-a1y(n-1)-a2y(n-2)+b0x(n)+ (10) 依据式(10),只需通过程序编写就可实现对数字陷波滤波器的应用。该数字陷波滤波器等效结构如图8所示。 在实验过程中,获取系统的共振频率为f=295 Hz,现在使用设计的陷波滤波器对覆晶旋转臂该共振点295 Hz进行过滤处理。根据抑制效果目标,设置陷波深度系数j为0.4,陷波宽度系数k为3,然后使用MATLAB绘制出滤波器特性,以及滤波前、后的系统频域特性,如图9所示。 从图9可以看出:抑制前,共振频率点的幅值为-10 dB,当系统加入陷波滤波器后,其幅值衰减为-27.5 dB,说明共振频率点被抑制,陷波滤波器能够对覆晶旋转驱轴起到共振抑制作用,有效解决系统共振问题。 图8 数字陷波滤波器等效结构 图9 滤波器对覆晶旋转轴的共振抑制实验(伯德图) 针对覆晶旋转轴的共振模态问题,将其转化为共振特性的获取和改进型滤波器的设计问题,利用可以有效调节滤波深度和滤波宽度的特点以应对多工况振动模态的变化。实验表明,所设计的改进型陷波滤波器可调性高,能有效抑制共振频率点,解决覆晶旋转轴的共振问题。


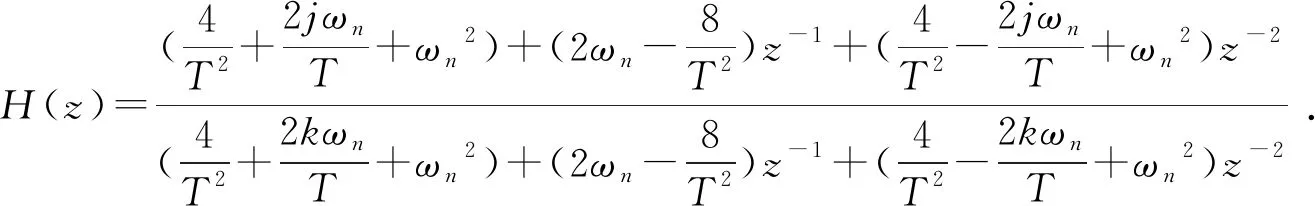
b1x(n-1)+b2x(n-2).4 共振抑制实验结果分析

5 结论
