基于修正S-N曲线的电池包支架疲劳仿真影响因素分析研究
2020-08-25闫鹏飞
闫鹏飞
(一汽丰田技术开发有限公司 天津300462)
0 引 言
车辆性能开发过程包含安全性能开发、强度性能开发、NV 性能开发、CFD性能开发等,因与车辆的品质息息相关,直接影响到品牌在市场上的核心竞争力,所以各大厂商都十分注重这些方面的研发与品质管理。同时,车辆的疲劳性能直接体现该品牌车辆在市场上的行驶里程,这是用户非常关心的品质参数,因而在车辆研发过程中,准确地判断车辆的疲劳性能显得尤为重要[1]。
本文结合一汽丰田某款纯电动客车的电池包支架搭载的疲劳仿真开发为例,从 S-N曲线角度研究影响车辆疲劳性能的参数。S-N曲线是评价车辆疲劳性能不可避免的最主要的影响因素[2],若缺少材料的S-N曲线,将很难对车辆的疲劳性能做出判断。本文针对 S-N曲线方面展开研究,为车辆疲劳性能的仿真开发提供参考。
1 电池包支架仿真中S-N曲线的修正
1.1 S-N曲线
我们通常所说的材料的 S-N曲线是使用光滑试棒做成的标准件,在拉压弯扭作用下的疲劳寿命表示曲线,如图1所示。

图1 材料S-N曲线示意图Fig.1 Diagram of material S-N curve
1.2 修正S-N曲线模型
一般汽车零部件都是经过相应的加工精度和热处理工艺的部品,其结构也都不尽相同,因此仅仅使用材料试棒的 S-N曲线进行疲劳仿真分析,与真实的情况存在较大出入。为了提高仿真分析精度,通常的做法是会对材料的 S-N曲线进行修正。对 S-N曲线修正的方法通常有 2种,第 1种是基于 Miner Modified准则,即在疲劳极限以下的部分按照斜率为2k-1进行修正;第 2种是基于 Miner Elementary准则,即在疲劳极限以下的部分按照原斜率 k进行延伸,如图2所示。

图2 不同修正方法的S-N曲线示意图Fig.2 Schematic diagram of S-N curve with different correction methods
2 基于 S-N曲线的某电池包支架疲劳强度仿真分析比较
根据从北京通县采集的路谱数据,结合企业开发目标公里数进行数据处理,在本次仿真分析中,通过企业标准进行数据转换,最后给电池包一个振动载荷谱,用于疲劳仿真计算,将有限元计算结果与 S-N曲线进行比较,根据其对应的循环次数及目标值循环次数,得到其损伤值(d1),计算方法如图3所示。
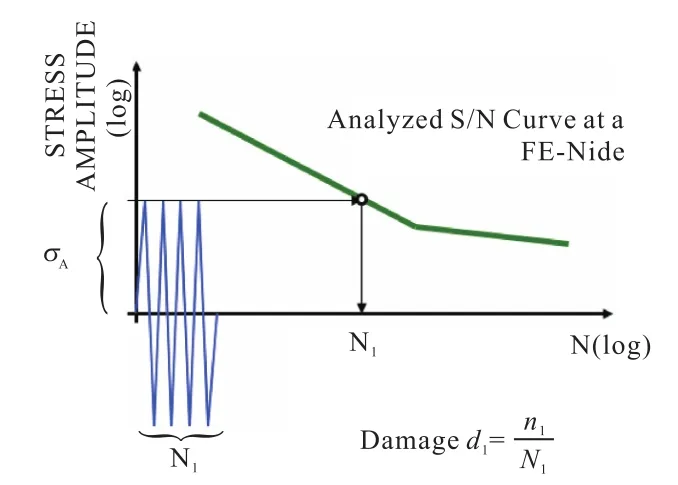
图3 损伤值计算示意图Fig.3 Diagram of damage value calculation
其中,Damage(d1)值是根据 Miner准则来计算的有限元模型的损伤值[3],本文所述的不同修正方法的S-N曲线为变量,其余均为相同的设置参数。
2.1 基于Minner-Original的S-N曲线疲劳仿真结果
通过对该电池包局部模型的有限元分析,支架安装点区域的Z方向的有限元应力结果如图4所示。
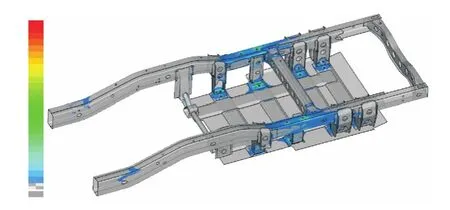
图4 电池包支架计算应力图Fig.4 Calculation stress diagram of battery pack bracket
本次研究主要关注点在螺栓连接部位。因为螺栓的刚度较大,并且采用了凸焊螺母的形式,为了便于后期电池包的维修,又必须是可拆卸部品,所以螺栓安装点的疲劳强度性能直接关系到该电动车的品质和今后在用户处的口碑。以图中某一个螺栓安装点为例进行研究分析,将局部应力结果放大后如图 5所示。
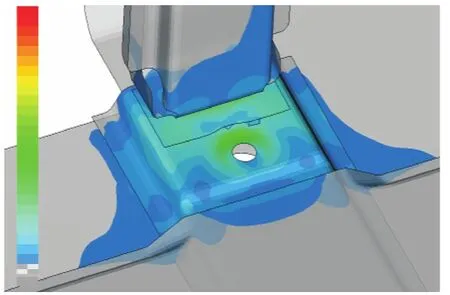
图5 螺栓孔应力图Fig.5 Diagram of bolt hole stress
该螺栓孔处的应力值 σ1= 2 02MPa,结合材料的基于 Minner-Original的 S-N曲线,计算出其疲劳寿命,循环次数n1=6.1万次。我们的 S-N曲线对应的目标循环次数为 10万次,因此其损伤值0.61。接下来我们进行基于修正的 S-N曲线的损伤值计算。
2.2 基于 Minner-Elementary修正的 S-N曲线疲劳仿真结果
通常由于加工工艺等因素的影响,在疲劳仿真分析中会进行 S-N曲线的修正,虽然精度会有所提升,计算时间和工作量也会相应增加。为了便于研究其修正 S-N曲线对于分析结果的影响趋势,本文以基于Minner-Elementary修正的S-N曲线方法为例进行说明。将模型导入到FEMFAT软件中进行计算,计算参数为与2.1同样的应力幅值(Stress Amplitude)和循环次数(N),计算模型如图6所示。
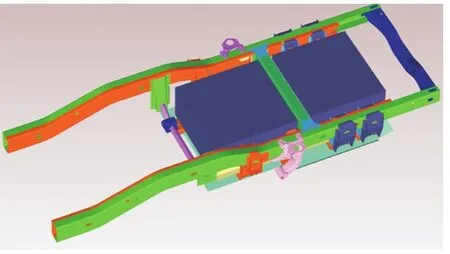
图6 损伤值计算模型图Fig.6 Diagram of damage value calculation model
S-N曲线进行修正前后对比如图7所示。
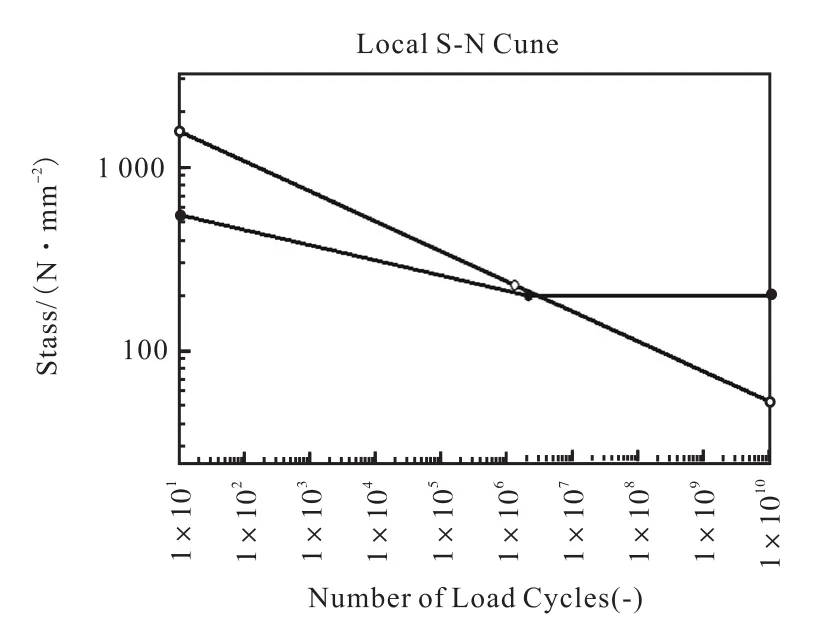
图7 S-N曲线修正前后对比图Fig.7 Comparison before and after S-N curve correction
前与上述修正相应,Haigh图也会进行相对应的修正,其修正后对比如图8所示。
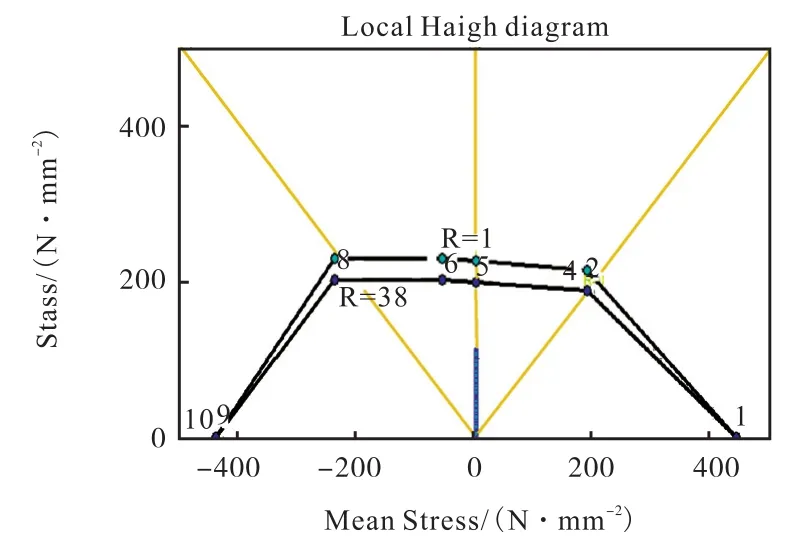
图8 修正前后Haigh图Fig.8 Haigh diagram before and after correction
通过对与 2.1同一位置的螺栓孔处的损伤值进行分析可知,螺栓孔附近的最大损伤值的位置,与2.1计算的结果保持一致,结果如图 9所示。该损伤值最大的节点载荷和损伤值结果见图10。
该支架基于Minner-Elementary修正的S-N曲线损伤值的实际循环次数n2=6.1万次,保持不变,其损伤值计算结果为万次。那么可以看出,材料 S-N曲线经过修正后,再次计算时修正后的危险点的可循环次数[N]会增大,其损伤值则有一定幅度的降低。
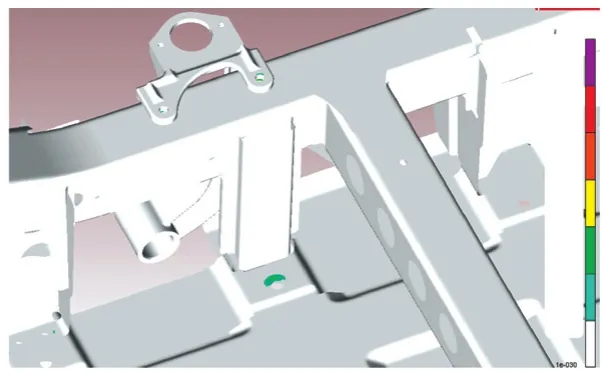
图9 螺栓孔损伤值分布图Fig.9 Distribution of bolt hole damage value
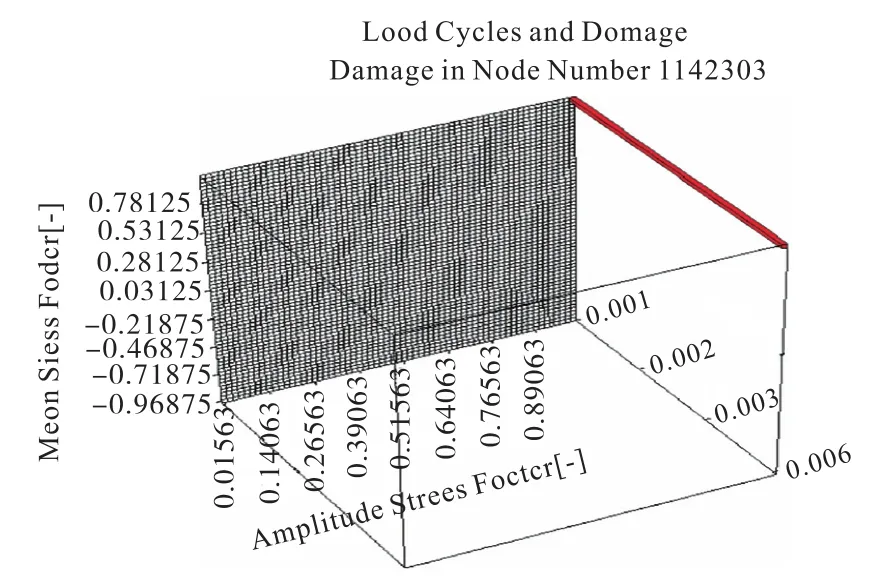
图10 载荷和损伤值结果图Fig.10 Result chart of load and damage value
2.3 结果比较分析
首先以与 2.2同样的方法计算出该支架基于Miner-Modified修正的S-N曲线的损伤值结果、循环次数结果,然后对比 3种分析方法的结果,得到其差异情况如图11所示。
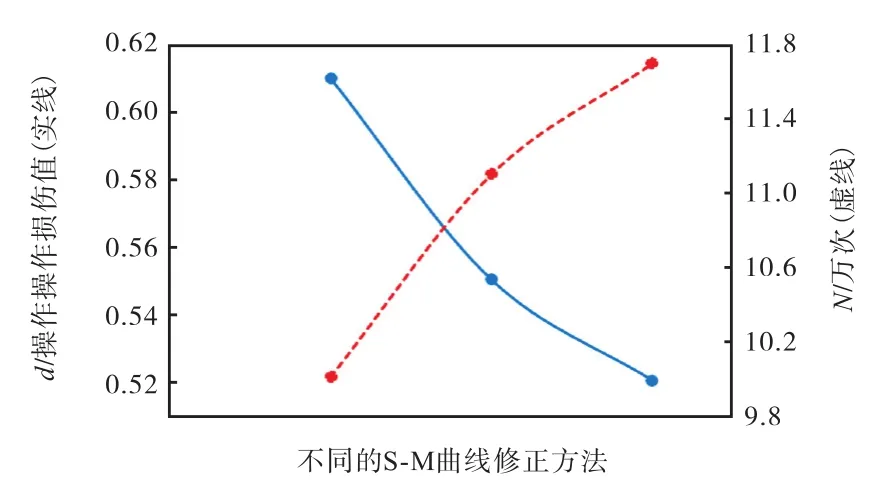
图11 损伤值结果对比图Fig.11 Comparison of damage value results
其中,对 S-N曲线的k值修正最大的 S-N曲线的损伤值结果与材料未经修正的损伤值结果相比有下降趋势,下降幅度约为 14.8%,而修正幅度较小的基于Miner-Modified修正的S-N曲线的损伤值结果也同样有下降趋势,下降幅度约为 9.8%,与理论预期结果相同,符合真实情况。这表明,企业可以根据不同的情况进行 S-N曲线的修正,结合加工工艺、企业安全系数等相关因素进行疲劳仿真分析。
3 结论及展望
①通过对疲劳仿真分析中最根本的影响因素 SN曲线的修正影响进行分析,定性验证了影响趋势与理论认知的一致性,为今后的疲劳仿真开发评价提供参考。
②下一步可以针对多点、多模型等大量的疲劳仿真分析数据结果进行分析研究,在明确分析精度的前提下,从提高分析影响因素的统计学研究层面进行验证研究。
