近海盐雾区钢筋混凝土圆形截面构件承载力退化研究
2020-08-24谷音李攀
谷音,李攀
(福州大学 土木工程学院,福州 350108)
钢筋混凝土圆柱暴露在氯盐环境中,氯离子通过混凝土基质渗透到钢筋表面,使得钢筋锈蚀,同时引起保护层混凝土开裂甚至剥落[1],从而导致截面承载力出现退化。目前,腐蚀钢筋混凝土截面剩余承载力评估方法已被很多学者关注。Akiyma等[2]通过OpenSees有限元模型,获得了腐蚀矩形桥墩截面承载力曲线。Tapan等[3]考虑腐蚀导致的钢筋和混凝土之间粘结能力退化,通过欧拉公式来评估锈蚀钢筋的临界受压屈服应力,获得不同腐蚀情况下钢筋混凝土矩形截面轴力-弯矩相关曲线。Guo等[4]将矩形桥墩截面划分为离散性纤维单元,进一步获得氯盐环境下钢筋混凝土矩形柱在不同服役期的轴力-弯矩相关曲线。目前,不同腐蚀程度下混凝土柱矩形截面剩余承载力评估方法的研究已经相对完善。然而,已有文献对圆形截面剩余承载力的研究较少。
为了确保混凝土圆柱在服役期的安全性,合理预测钢筋混凝土圆柱开始腐蚀时间显得尤为重要。Colepardi等[5]考虑扩散系数为常数,首次求解出氯离子在一维坐标下的扩散方程。Manget等[6]通过试验发现氯离子扩散系数随着时间增加而逐渐降低,可表达为时间函数,并对Colepardi等[5]提出的扩散模型进行更新。近年来,越来越多的学者开始考虑截面形状对氯离子扩散的影响。Val等[7]采用有限差分方法对二维Fick扩散方程进行求解,获得不同位置处钢筋开始锈蚀时间。胡守旺等[8]采用有限元软件(Comsol Multiphysis)模拟暴露氯盐环境下不同服役期的预应力T梁中钢筋表面氯离子浓度。Shafei等[9]通过利用有限元软件模拟三维坐标下混凝土圆柱中钢筋开始腐蚀时间。相比复杂的计算方法及有限元建模,简洁的数学模型更方便且更有效地预测氯离子在混凝土中扩散。对于混凝土圆柱,Morga等[10]考虑扩散系数为常值,采用变量分离方法对极坐标下Fick二维扩散方程进行求解,获得了圆形扩散模型。Song等[11]指出,随着混凝土水化作用持续发生,毛细孔率逐渐降低,扩散系数随着服役时间增长而改变。通过对6座不同龄期普通硅酸盐混凝土的扩散系数实测数据进行回归分析,Pack等[12]验证了扩散系数强烈依赖服役时间。汪加梁等[13]考虑扩散系数为时变函数,对圆形扩散模型进行了更新。Morga等[10]与汪加梁等[13]研究结果表明,对于混凝土圆柱,混凝土表面氯离子浓度值越小,圆形截面半径对钢筋开始腐蚀时间的影响越明显。McGee等[14]根据对位于Tasmania的1 158座桥梁的研究,结果表明,混凝土表面氯离子浓度随着离海岸线距离增加而逐渐降低。Akiyma等[15]也指出空气中氯离子浓度随着海岸线距离显著降低。由此可见,随着海岸线距离增加,混凝土圆柱形状对评估钢筋开始腐蚀的影响越显著。
笔者研究了不同海岸线距离混凝土圆形截面形状对评估钢筋开始腐蚀时间的影响,进一步分析了形状对评估截面承载能力退化率的影响,给出了更加合理评估钢筋混凝土圆柱承载力退化率的建议。
1 钢筋混凝土圆柱开始腐蚀时间
1.1 氯离子扩散模型
假设混凝土基质为均匀材料,氯离子在圆形截面中扩散可采用极坐标下Fick第二定律来描述,如式(1)所示。
(1)
式中:D为氯离子扩散系数;t为扩散时间;C(ρ,t)为距离圆心ρ处t时刻的氯离子浓度;考虑氯离子扩散系数为时间t的函数,如式(2)所示[6]。
(2)
式中:m为混凝土老化系数,m=2.5(w/c)-0.6,其中,w/c为水灰比;Dref为养护龄期tref对应的氯离子扩散系数,一般tref取28 d,D28可表达为D28=10-12.06+2.4(w/c)[16]。
氯离子在圆形截面扩散中满足如下假定:1)表面氯离子浓度为常值;2)截面中氯离子浓度分布满足轴向对称;3)混凝土基质中初始氯离子浓度为0。
对C(ρ,t)采用分离变量C(ρ,t)=φ(ρ)ψ(t),结合式(2),式(1)可更新为
(3)
对式(3)进行变形
(4)
式(4)中,等号左侧仅为变量t的函数,右侧仅为ρ的函数。当且仅当左右两边的方程等于相同常数λ2时,等式(4)成立。式(4)可变形为
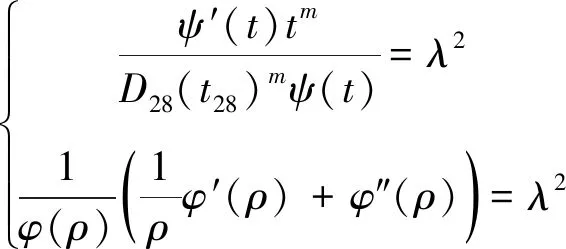
(5)
对方程组(5)中等式分别求解,基于氯离子在混凝土圆形截面扩散假设,氯离子在圆形截面中的扩散模型可更新为
Ccir(ρ,t)=
(6)
式中:C0为混凝土暴露在环境中的表面氯离子浓度;R为混凝土圆柱半径;J0为零阶贝塞尔函数;J1为一阶贝塞尔函数;αn是方程J0(Rαn)=0的根。
若忽视圆形截面对氯离子扩散的影响,评估钢筋表面氯离子浓度时,平板扩散模型如式(7)所示[6]。
(7)
式中:x为保护层厚度;erf为高斯误差函数。
为了对比平板扩散模型与圆形扩散模型,文献[17]定义了Ccir(R-x,t)/Cslab(x,t),其中R为圆形截面半径,分析了表面氯离子浓度C0、扩散系数D28、老化系数m、保护层厚度x、半径R、扩散时间t参数对Ccir(R-x,t)/Cslab(x,t)比值的影响。通过参数分析结果,圆形扩散模型可被简化为修正平板扩散模型,如式(8)所示。
Ccir(x,t)=(1.8R-1.3x+1)·
(8)
平板扩散模型评估开始腐蚀时间Tslab,表达式为
(9)
式中:erf-1为高斯误差反函数;Ccr为氯离子浓度阈值;C0为混凝土表面氯离子浓度。
考虑圆形截面对开始腐蚀时间的影响,通过修正平板扩散模型评估开始腐蚀时间,表达式为
(10)
1.2 开始腐蚀时间计算
为了提高结构的使用耐久性,《混凝土结构耐久性设计与施工指南》(CCES 01-2004)[18]对暴露在近海盐雾区混凝土结构构造做出了具体规定。当距离海岸线0.1 km内时,为重度盐雾区,混凝土柱的最大设计水灰比为0.36,最小保护层厚度为55 mm;当距离海岸线0.1 km外至0.3 km内时,为轻度盐雾区,最大设计水灰比为0.4,最小保护层厚度为50 mm。
考虑钢筋混凝土结构处于最易遭受氯离子腐蚀状态,保护层厚度取最小设计值,水灰比取最大设计值。待确定参数表面氯离子浓度与浓度阈值具有较大随机性。为了简化分析,其参数取具有一般水平的均值。根据文献[19],氯离子腐蚀的浓度阈值的均值为0.9 kg/m3,混凝土表面氯离子浓度均值为海岸线距离dcoast函数,如式(11)所示。
(11)
研究半径为40、60、80、100 cm的钢筋混凝土柱。通过式(9)与式(10)分别评估不同dcoast下腐蚀开始时间,结果如图1所示。当dcoast超过0.1 km时,钢筋开始腐蚀时间随着海岸线距离显著增加。修正平板扩散方程与平板扩散方程评估开始腐蚀时间的差值如图2所示。当混凝土圆柱暴露在轻度盐雾区时,开始腐蚀时间差值保持恒定且小于5 a,当dcoast大于0.1 km时,该差值逐渐增加。图2中不同dcoast所对应的开始腐蚀时间差值见表1。
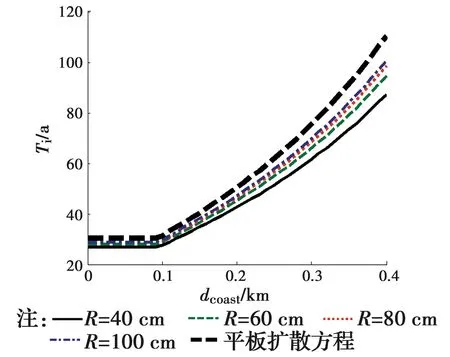
图1 海岸线距离dcoast所对应的钢筋腐蚀开始时间TiFig.1 The time to corrosion initiation of RC circular column corresponding to dcoast
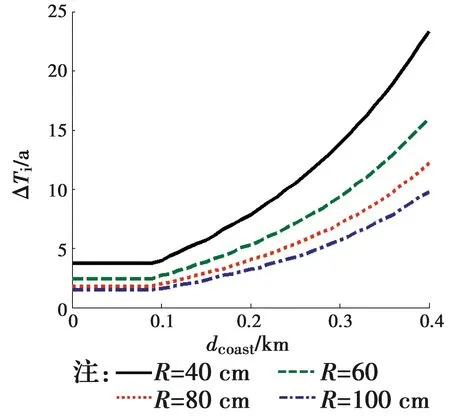
图2 采用修正平板扩散方程与平板扩散方程所产生的开始腐蚀时间差值ΔTiFig.2 The difference value between the time to corrosion initiation estimated by modified slab diffusion model and this time estimated by original slab one
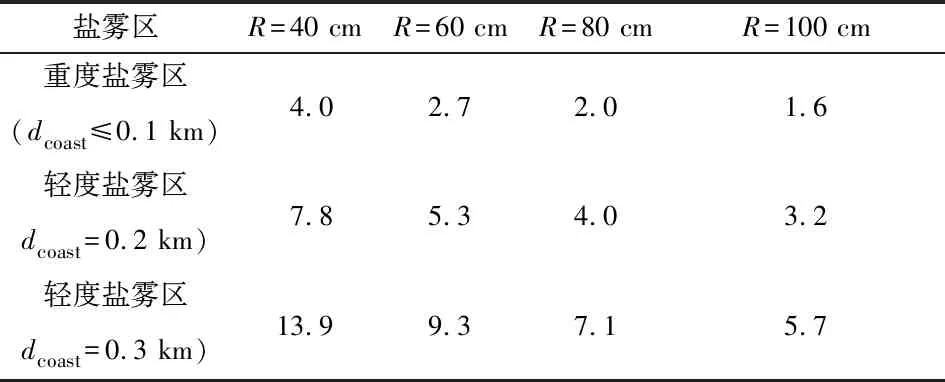
表1 不同半径下dcoast所对应的开始腐蚀时间差值(ΔTi/a)Table 1 The difference of the time to corrosion initiation corresponding to dcoast at a series of radius
2 腐蚀钢筋混凝土圆柱截面承载力模型
2.1 材料性能退化模型
Du等[20]提出了腐蚀钢筋屈服强度退化模型,如式(12)所示。
fy(t)=(1-0.5η(t))fy0
(12)
式中:fy(t)为腐蚀时间t钢筋剩余屈服强度;fy0为未腐蚀钢筋屈服强度;η(t)为t时刻钢筋质量损失率。
自然环境下腐蚀钢筋主要以点蚀形态存在,如图3所示。若钢筋腐蚀形态沿长度方向保持一致,η(t)可采用截面积损失率表示。
(13)
式中:D0为正常钢筋直径;As(t)为钢筋剩余面积,计算模型如式(14)~式(18)所示[21]。
(14)
(15)
(16)
(17)
(18)
式中:p(t)为t时刻局部锈蚀深度,根据文献[22],具体表达式为
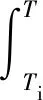
(19)
(20)
式中:R为局部腐蚀系数,均值为7.1。

图3 钢筋剩余面积计算示意图Fig.3 Schematic diagram of resiudal corroded area bar
锈蚀产物的体积膨胀,导致保护层混凝土开裂甚至剥落。Qi等[23]结合理论与试验结果,提出钢筋腐蚀量与保护层混凝土开裂宽度的半经验与半理论模型,如式(21)~式(23)所示。
Wc=Wc1+Wc2
(21)
(22)
(23)
式中:Wc为单位长度钢筋腐蚀量;γ为铁的密度,取为7.85 mg/mm3;ρ为体积膨胀系数,取值为3;c为保护层厚度;d为钢筋直径;w为保护层混凝土裂缝宽度;当混凝土E为混凝土弹性模量;fc为混凝土28 d抗压强度;α0、β0、α1、β1为修正系数。
当钢筋开始腐蚀后,保护层混凝土开裂宽度所对应的Wc与腐蚀开裂时间Tcr满足
Wc=γp(Tcr)
(24)
式中:V为钢筋腐蚀速率;p(Tcr)为开裂时间Tcr所对应的局部腐蚀深度。
当保护层混凝土开裂严重时,腐蚀速率增加,如式(25)所示[24]。
λ2(t)=(4.5-26λ1(t))λ1(t)
(25)
保护层混凝土剥落后,式(12)不再适用于评估腐蚀钢筋抗压强度。此时腐蚀钢筋临界受压屈服应力为[3]
(26)
式中:Es为腐蚀钢筋弹性模量,腐蚀对弹模的影响可以忽略;Is(t)为t时刻腐蚀钢筋截面惯性矩;Lexp为钢筋暴露长度。
由于Coronelli等[25]提出的保护层混凝土抗压强度退化模型不适用于圆形截面,当保护层混凝土未剥落时,假定保护层混凝土抗压强度不变。根据文献[26],当裂缝宽度到达极限值1 mm时,裂缝扩展严重,可认为保护层剥落,其抗压强度为零。考虑箍筋腐蚀对于约束混凝土的影响,在已知箍筋的剩余面积和屈服强度后,通过Mander模型来计算约束混凝土的抗压强度。
2.2 截面承载力计算公式
如图4所示,保护层混凝土采用抛物线本构,保护层混凝土峰值应力对应的应变为0.002,极限应变为0.003 3。考虑钢筋为理想弹塑性材料,采用双线性本构描述应力-应变关系。核心混凝土采用Mander模型计算应力-应变关系,细节见参考文献[27]。
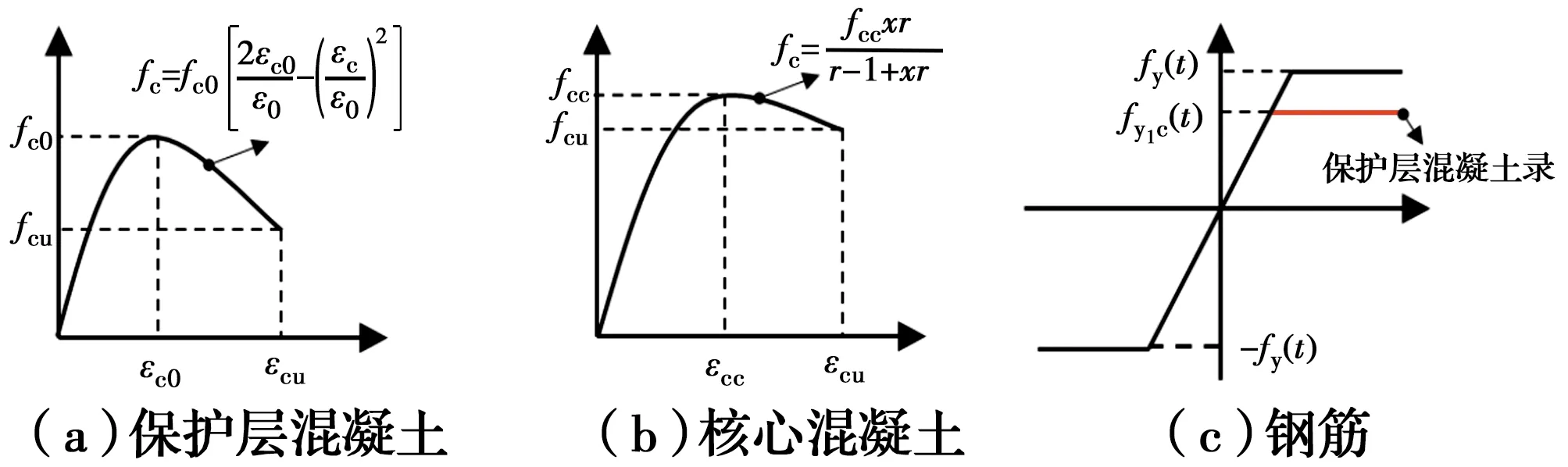
图4 材料应力-应变关系Fig.4 The relationship between the stress and strain of material
对于腐蚀后圆形混凝土截面,仍满足平行截面假定。图5中,εcu为保护层混凝土极限压应变;xc为混凝土截面受压高度;εsc与εst为钢筋压应变与拉应变。混凝土划分成若干个水平层状单元,每根钢筋作为单独单元处理。σco(i)为i单元处保护层混凝土抗压强度,σcc(i)为i单元处核心混凝土抗压强度,σsc(j)为j位置处钢筋抗压强度,σst(k)为k位置处钢筋抗压强度。当圆形截面划分条带层数量较多时,每个不规则水平层状条带简化为矩形单元,如图6所示。对于每个混凝土矩形单元,所提供的轴力Nc(i)与弯矩Mc(i)可表示为
(27)
(28)
Nc(i)=Nco(i)+Ncc(i)
(29)
Mc(i)=(R-id)N(i)
(30)
若划分混凝土条带层状单元不包含核心混凝土时,Ncc(i)变为0,Nco(i)重新表达为
(31)
整个圆形截面轴力和弯矩的平衡条件为
(32)
(33)
式中:p为混凝土条带层状单元数量;m为截面受压钢筋数量;n为截面受拉钢筋数量。
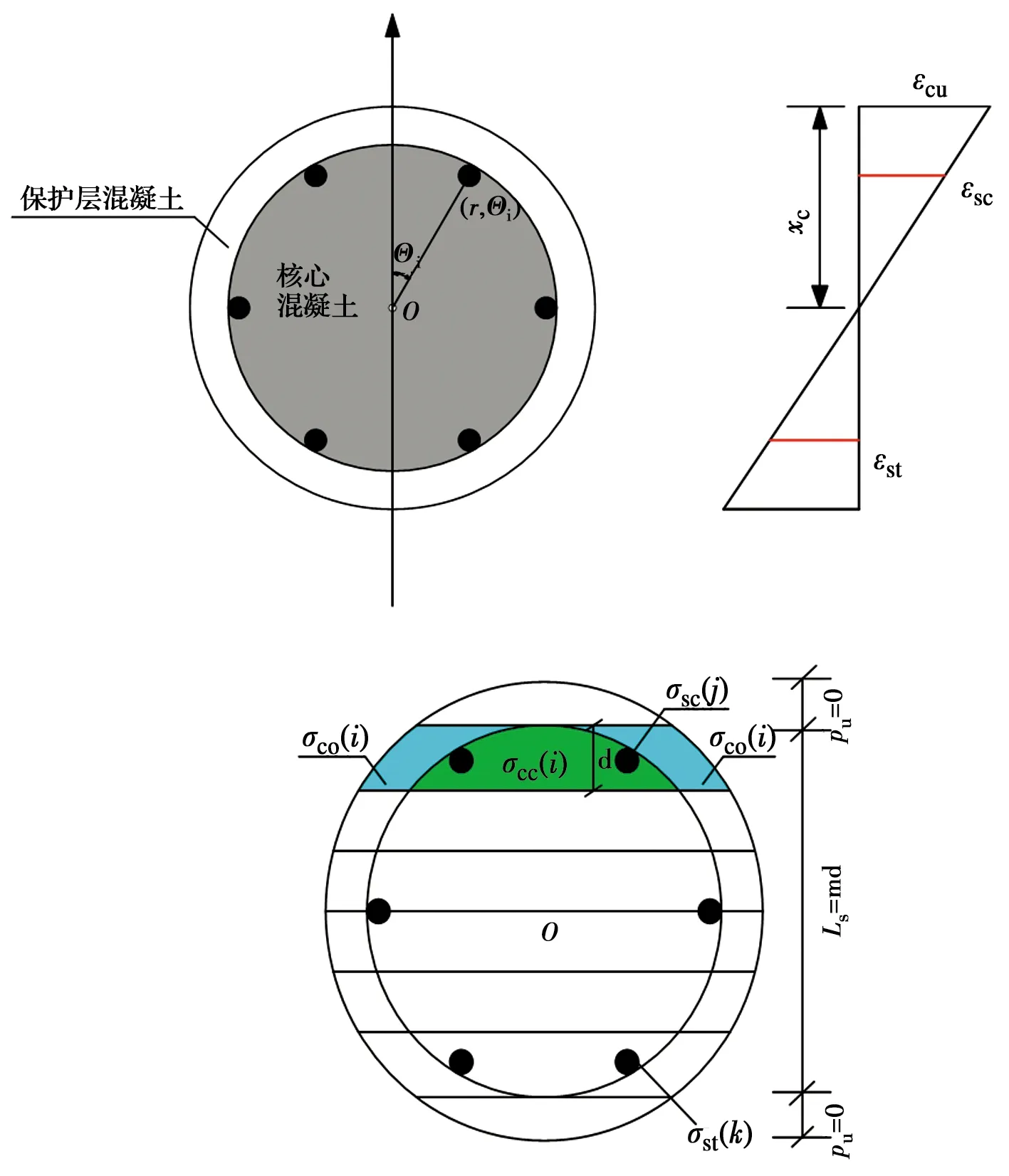
图5 钢筋混凝土圆形截面应变-应力分布及条带层划分Fig.5 The strain-stress distribution and layer element division of circular section of reinforced concrete
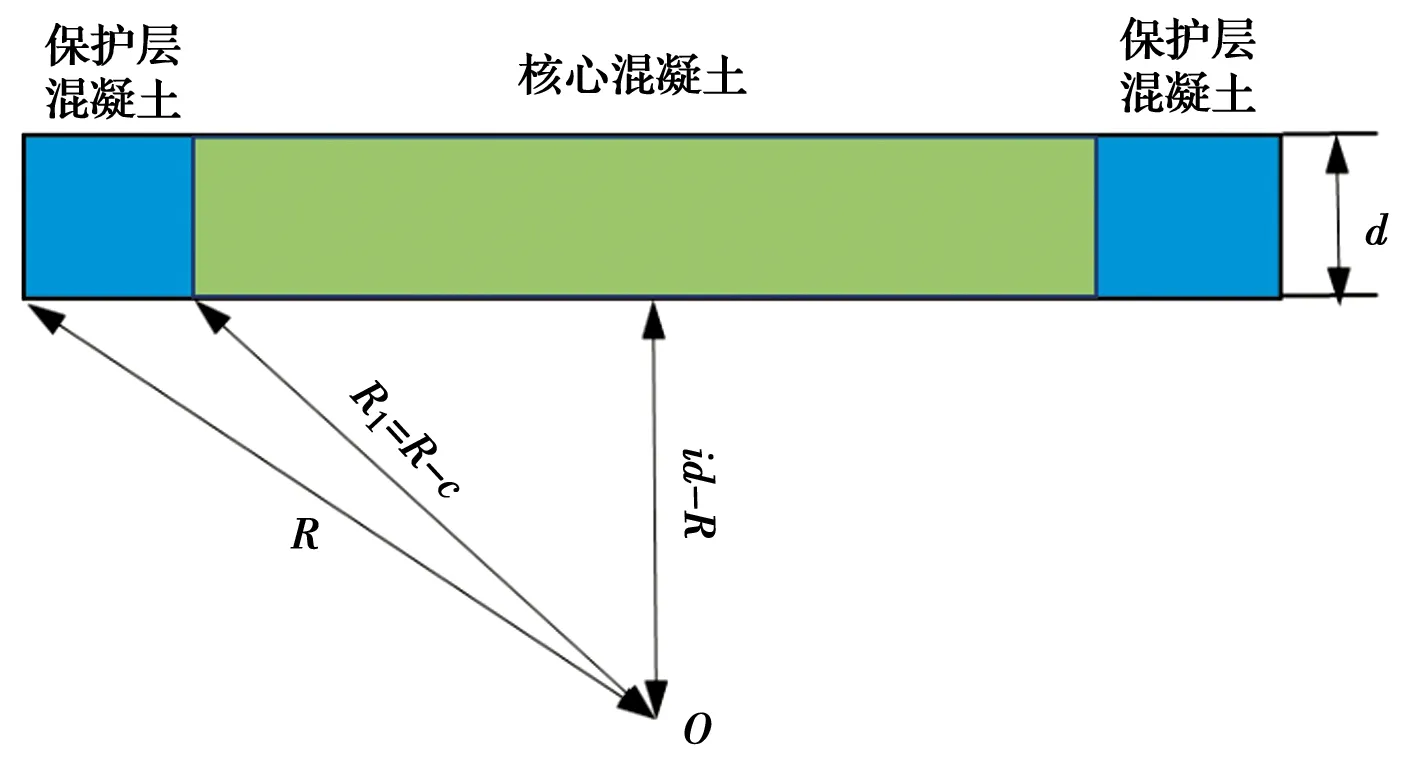
图6 第i个混凝土条带层示意图Fig.6 Schematic diagram of the ith concrete layer element
基于Matlab,编制混凝土圆柱截面弯矩承载力计算程序。给定截面轴向荷载Np,通过图7所示流程可得截面弯矩承载力。
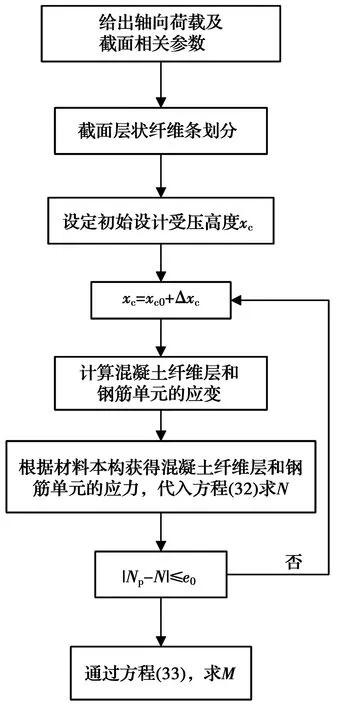
图7 计算指定轴力下截面弯矩承载力示意图Fig.7 Flow chart of calculating bending moment capacityunder specified axial force at circular across-section
2.3 模型验证
《混凝土结构设计规范》(GB 50010—2010)[28]对正常圆形截面承载力计算公式进行了详细描述。若钢筋腐蚀率为0,即钢筋未发生腐蚀的情况,将规范与笔者所提出的计算方法进行对比。假定钢筋混凝土圆柱截面半径为60 cm,保护层厚度为5 cm,截面配置24@25 mm、设计屈服强度为360 MPa的纵筋。箍筋采用直径为10 mm、间距为80 mm的HPB300,设计屈服强度为270 MPa。混凝土抗压强度分别取30、40、50 MPa。计算结果如图8所示。需指出的是,笔者考虑了截面处于轴心受压状态。在轴力-弯矩相关曲线中,弯矩为零对应为截面所能承受的最大轴力值。在弯矩为零附近未考虑水平直线段。
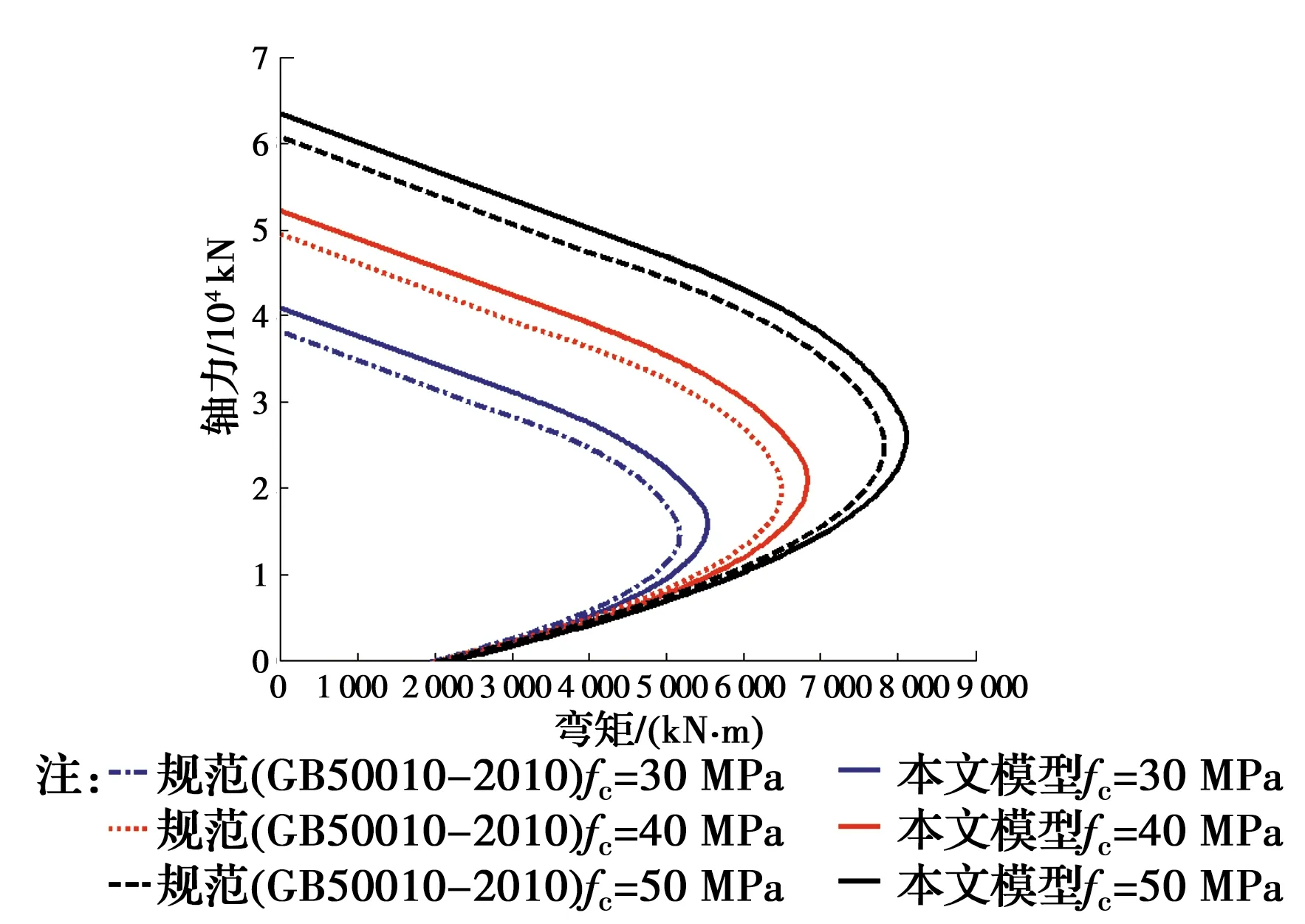
图8 规范(GB50010-2010)与本文计算模型对比Fig.8 Comparison between Code (GB50010-2010) and calculation method proposed in the paper
由图8可见,当竖向轴力较小时,采用的计算方法与规范计算结果吻合很好。当轴力增加时,混凝土受压高度增加,所对应的弯矩承载力大于规范计算值,这是由于规范中未考虑箍筋对核心的约束作用,核心混凝土强度取值与保护层混凝土强度一致。对比结果表明,计算方法对未腐蚀性圆形截面同样适用,一定程度上反映了腐蚀圆形截面承载力计算方法的合理性。
Ma等[29]设计了13个不同腐蚀程度的混凝土圆形柱来研究墩柱的力学性能退化规律。选取其中5个发生弯曲破坏的圆形桥墩试验信息进行对比。纵筋实测屈服强度为373.2 MPa,箍筋实测屈服强度为327 MPa,28 d混凝土实测抗压强度为32.4 MPa,加载高度为0.82 m。朱杰[30]对不同腐蚀程度的钢筋混凝土圆柱进行拟静力试验,构件均发生弯曲破坏。纵筋实测屈服强度为355.626 MPa,箍筋实测屈服强度为230.677 MPa,28 d混凝土实测抗压强度为30.43 MPa。加载高度为1.1 m,以上试验构件中的钢筋质量损失率与轴压比信息分别列于表2和表3中,试验样本的截面及配筋信息如图9所示。Ma等[29]试验信息中,未对箍筋腐蚀率进行描述。参考已有文献[31-32]试验结果,取箍筋腐蚀率为纵筋腐蚀率的2倍。

图9 试验样本构造图(单位:mm)Fig.9 The detail of experiment specimen (unit: mm)

表2 Ma等试验样本腐蚀率和轴压比信息Table 2 The specimens about corrosion degree and ratio of axial compression stress to strength by Ma et al

表3 朱杰试验样本腐蚀率和轴压比Table 3 The specimens about corrosion degree and ratio of axial compression stress to strength by Zhu
由于钢筋的不均匀腐蚀,试验样本的骨架曲线往往出现不对称现象。需指出的是,Ma等[29]试验资料中未给出正负加载方向的承载力信息。给出的承载力试验值为构件正负加载方向的均值。预测值与试验值的比值分布如图10(a)所示。朱杰[30]试验资料中,给出了构件正负加载时各自承载力试验值。预测值与正向承载力比值如图10(b)所示,预测值与负向承载力比值如图10(c)所示。通过统计分析,试验与预测比值分布的均值为0.88,方差为0.07。由此可见,预测值略低于试验值。在加速腐蚀过程中,纵筋的截面损失率沿墩高并非一致。保护层混凝土考虑完全剥落,受压钢筋采用欧拉公式即式(26)计算得到。实际情况中,保护层混凝土具有分布裂缝而并非完全脱落。这些原因导致预测值与试验值的比值分布具有较大离散性,且普遍小于1。文献[4]将腐蚀钢筋混凝土矩形截面承载力预测值与试验结果进行对比,结果表明了相同现象。考虑腐蚀截面的安全富余,该模型可作为圆形截面的剩余承载力评估。图10中的数据信息汇总见表4。
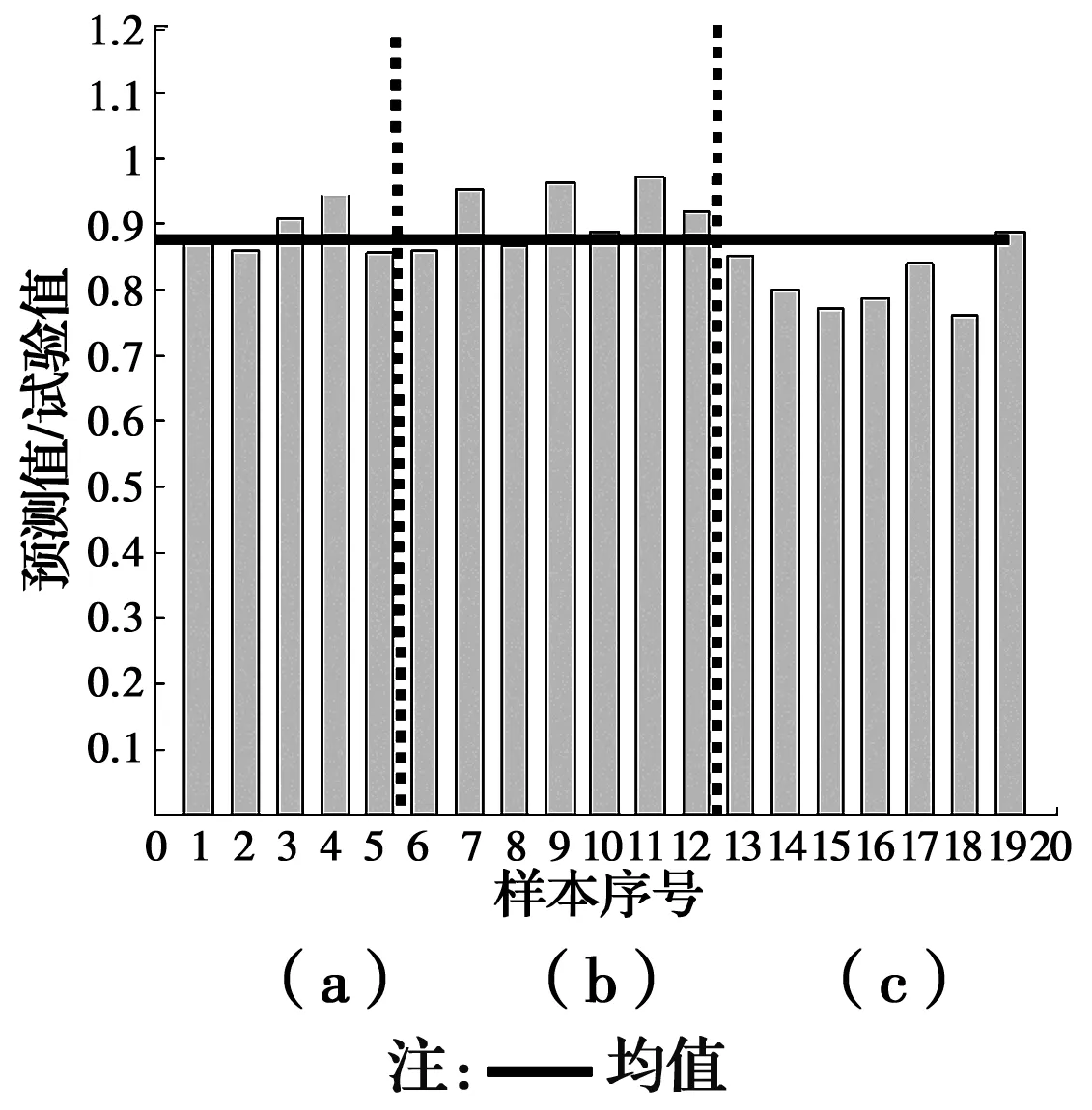
图10 预测值与试验值比值分布Fig 10 The distribution of the ratio of predicted value and experiment value
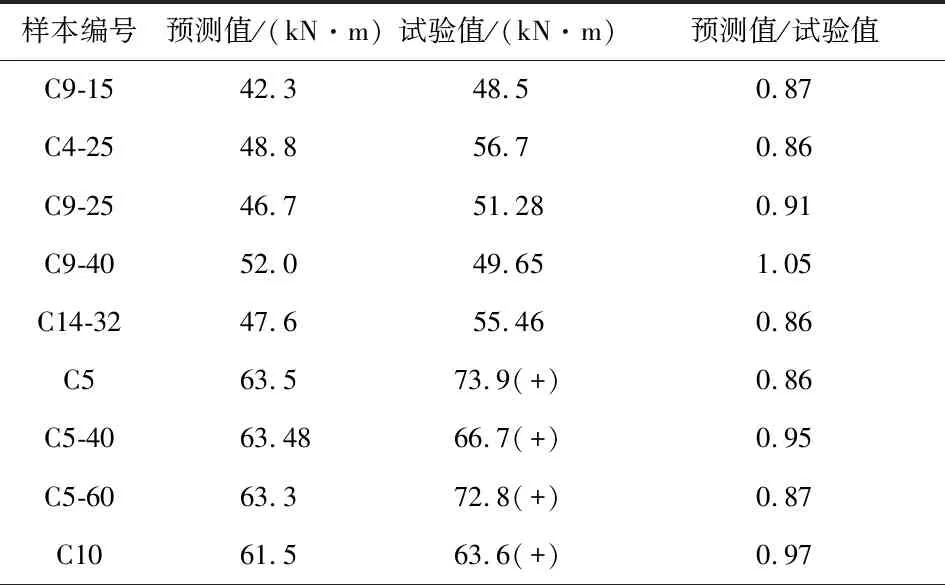
表4 试验样本的预测值与试验结果对比Table 4 Comparison between predicted value and experimental value of specimens
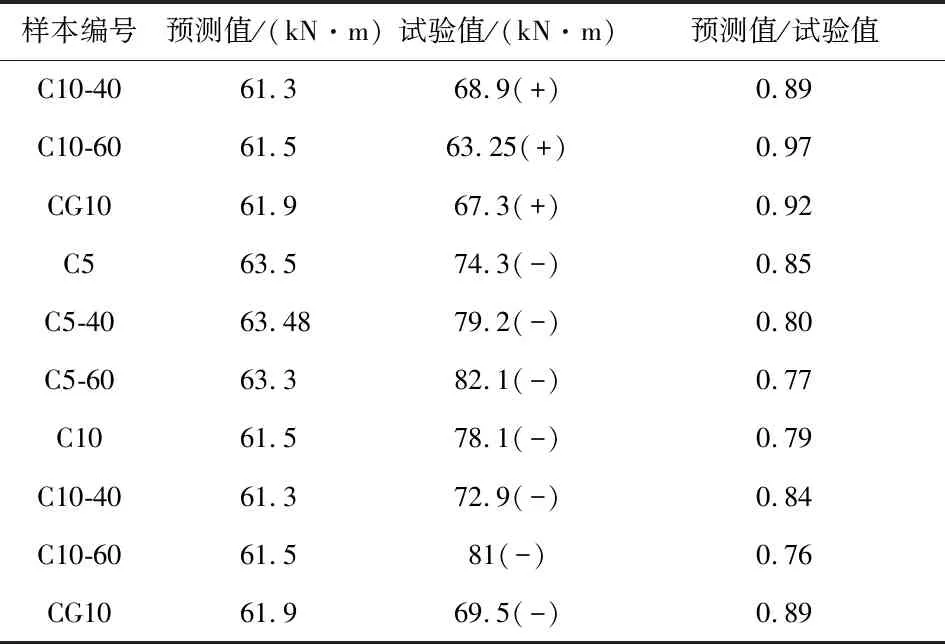
续表4
3 算例分析
以半径为40、60、80 cm的钢筋混凝土圆柱为研究对象,柱高4 m,采用C40混凝土,设计抗压强度为19.1 MPa,水灰比为0.4。混凝土保护层厚度为50 mm。当半径为40 cm时,配置12@25 mm的HRB400纵向钢筋,半径分别为60、80 cm时,截面分别配置24@25 mm与44@25 mm的HRB400纵向钢筋,纵筋设计屈服强度为360 MPa。箍筋采用直径为10 mm、间距为80 mm的HPB300,设计屈服强度为270 MPa。通过式(21)~式(24)可得,钢筋开始腐蚀后,保护层混凝土剥落时间为3.6 a。不同锈蚀时间Tc下圆形截面时变轴力-弯矩相关曲线如图11所示。

图11 钢筋锈蚀时间对截面N-M曲线影响Fig.11 The effect of corrosion time on N-M curve of RC circular column
由图11可见,当保护层混凝土剥落时,截面承载力出现骤降。选取截面最大轴向承载力Nmax,最大弯矩承载力Mmax以及截面轴力为零对应的弯矩承载力M0作为研究对象。基于图11中数据,Nmax、Mmax及Nmax在不同腐蚀时间时所对应的退化率如图12。由图12可见,对于M0,不同锈蚀时间下,各半径所对应的退化率基本保持一致。然而,对于Mmax和Nmax,半径越小,相同锈蚀时间所对应的退化率越高。对比M0、Mmax和Nmax,截面M0退化程度最为显著,其次为Mmax。这是由于截面受压高度越大,半径越大,钢筋对承载力的贡献越小,腐蚀对截面承载的影响越小。从拟合方程可见,退化率与锈蚀时间很好地满足了线性关系,且不同半径下,退化率随锈蚀时间增长速率基本相同。
由图2和图12可见,采用平板扩散模型将高估钢筋开始腐蚀时间,从而低估截面承载力的退化率。由于M0的退化程度最为明显,通过图12(a)中的拟合方程,不同海岸线距离下所对应的M0退化率差值如图13所示。从图13可以看出,对于重度盐雾区,各半径所对应的退化率差值均小于4%。随着海岸线距离增加,退化率差值逐渐增加,采用平板扩散模型对评估承载力退化率的影响逐渐增加。对于轻度盐雾区,图12中不同半径所对应的退化率差值见表5。由表5可见,当半径为40 cm时,退化率差值的均值为6.6%。当半径增加为60 cm时,差值降低到4.2%。
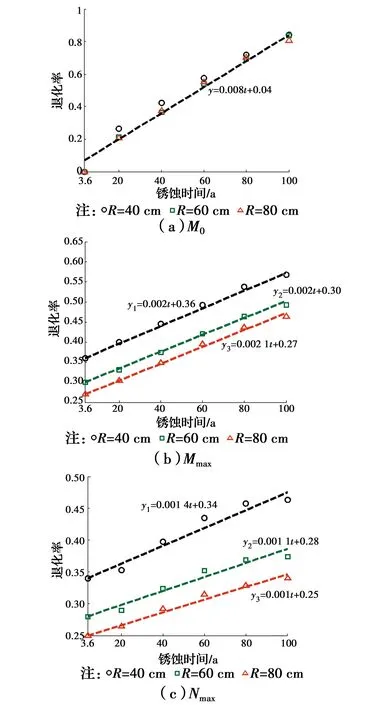
图12 钢筋锈蚀时间对M0、Mmax、Nmax的退化率影响Fig.12 The effect of corrosion time on the degradation rate of M0、Mmax、Nmax
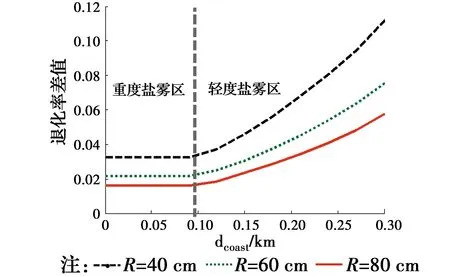
图13 截面M0退化率差值随海岸线距离变化图Fig.13 The difference value of bearing capacity M0 degradation rate varying with dcoast

表5 不同海岸线距离dcoast下M0退化率差值Table 5 The difference of M0 degradation rate under a series of dcoast
4 结论
推导与验证了腐蚀钢筋混凝土圆形截面承载力计算模型。考虑近海盐雾区截面形状对钢筋开始腐蚀时间的影响,对比了分别采用修正平板扩散模型与平板扩散模型对评估钢筋混凝土圆柱截面承载力退化率的影响,得到如下结论:
1)采用平板扩散模型将高估近海盐雾区钢筋混凝土圆截面中钢筋开始腐蚀时间。海岸线距离越大、半径越小,高估现象越明显。
2)保护层混凝土剥落,使得截面承载力出现急剧下降。钢筋锈蚀对轴力为0所对应的弯矩承载力M0的影响最为明显。随着半径增大,钢筋腐蚀对截面承载力的影响逐渐减小。
3)钢筋混凝土圆柱在重度盐雾区时,采用平板扩散模型所引起的截面承载力退化率差值小于4%,可以直接采用平板扩散模型评估钢筋开始腐蚀时间。位于轻度盐雾区时,当半径为40 cm,该承载力退化率差值的均值为7%,当半径为60 cm,该差值的均值变为5%左右。为了控制差值在5%以内,当钢筋混凝土圆柱半径小于等于60 cm且暴露在轻度盐雾区时,建议使用修正平板扩散方程评估圆柱钢筋腐蚀开始时间,进一步评估截面剩余承载力。
