摆式电涡流TMD-钢框架结构的耦合计算方法与减震分析

潘毅，包韵雷，国巍，陈业宏

(1. 西南交通大学 a. 土木工程学院；b. 抗震工程技术四川省重点实验室，成都 610031；2.中南大学 土木工程学院，长沙 410075；3.同济大学 土木工程学院，上海 200092)

调谐质量阻尼器(Tuned Mass Damper，简称TMD)作为一种被动式吸能减振装置，在结构减振领域得到广泛应用。TMD由于性能稳定、结构简单、易于调节自身刚度、便于安装等特点，可以满足结构任意水平方向和不同频段的振动控制需要，多应用于楼盖的人致振动控制与桥梁、高层建筑的风致振动控制中[1-4]。李爱群等[5]在MTMD减震机理的基础上提出了考虑人体舒适度的大跨楼盖MTMD设计方法，可以降低大跨楼盖的振动，提高舒适度。Fujino等[6]将TMD应用到东京湾跨海大桥的风振控制中，实测结果表明了TMD能够有效抑制其低阶涡激振动。徐怀兵等[7]将TMD应用于高层建筑风振控制中，通过设置主被动可切换的混合TMD，有效控制了结构动力响应。相比于在人致荷载和风荷载控制中的应用，TMD应用于建筑结构减震的研究还比较少。叶献国等[8]将TMD应用于混凝土巨型框架结构的减震设计中，并进行了缩尺模型的振动台试验，结果表明TMD有较好的减震效果。秦丽等[9]提出了一种变摩擦TMD，解决了常摩擦TMD控制效果不稳定的问题，有效降低了结构的地震响应。传统的TMD大多采用液体黏滞阻尼器作为阻尼单元，存在易渗漏、阻尼参数不易调节、后期维护困难等不足[10]，而摆式电涡流TMD是一种采用电磁阻尼作为阻尼单元的新型TMD，具有不依靠液体黏滞力耗能、不需要复杂机械连接、阻尼系数易于调节、制造安装与后期维护方便等优点[11]。Bae等[12]、Bourquin等[13]、Lu等[14-15]、汪志昊等[16]已对摆式电涡流TMD的减振性能和阻尼比等设计参数进行了试验研究，并在人行桥的人致振动控制和拱桥刚性吊杆、高耸结构、高层建筑的风振控制等领域得到了应用[17-20]。

目前，在摆式电涡流TMD的研究中，存在几个不足：1)较少对其抗震性能及工程应用进行研究，即使采取振动台试验，但受限于试验条件，也往往采用缩尺模型，不能完全反映工程结构抗震性能的真实情况，得不到摆式电涡流TMD的实际减震性能。2)多数研究是基于其自身的设计参数，进行的单个TMD研究，鲜有将摆式电涡流TMD与工程结构进行联合计算分析，且结构多为简化模型，未考虑结构抗震的实际需求。3)摆式电涡流TMD具有阻尼时变的特性，现有分析软件难以完成摆式电涡流TMD与结构的耦合计算，也缺乏有效的计算方法。针对上述情况，笔者提出一种基于联合仿真的耦合计算方法，以模拟摆式电涡流TMD阻尼的时变过程，并建立摆式电涡流TMD-钢框架结构模型，计算其在罕遇地震作用下的结构响应，分析层位移、层间位移角、层剪力、层加速度随TMD质量比的变化规律，并与无摆式电涡流TMD的钢框架结构进行比较，分析摆式电涡流TMD质量比对钢框架结构减震性能的影响，并给出合理的TMD质量比建议。

1 摆式电涡流TMD的组成

摆式电涡流阻尼器一般放置于结构的顶层，其组成部件由下至上分别为导磁钢板、永磁体、导体板、调谐质量块、吊索，如图1所示。导磁钢板固定于屋面结构板，其上放置若干永磁体，可充分利用钢的导磁性，使磁感线向此处汇集，磁感应强度得以加强，且磁泄露量减小。永磁体置于导磁钢板上表面，用于产生磁场，永磁体的充磁方向为上下充磁，相邻永磁体充磁方向相反。导体板采用铜为材料，用于产生电涡流及电磁阻尼，当地震时结构振动，导体板随着调谐质量块一起振动，其切割磁感线产生电涡流，形成阻碍导体板与永磁体二者相对运动的电磁阻尼力。调谐质量块用于提供摆式电涡流TMD的质量，采用铁为材料，同样利用铁的导磁性，使磁感线向此处汇集，磁感应强度得以加强，且磁泄露量减小。吊索下方连接调谐质量块，上方固定于支架上，材料采用预应力钢绞线，保证其能承担质量块摆动时产生的拉力。

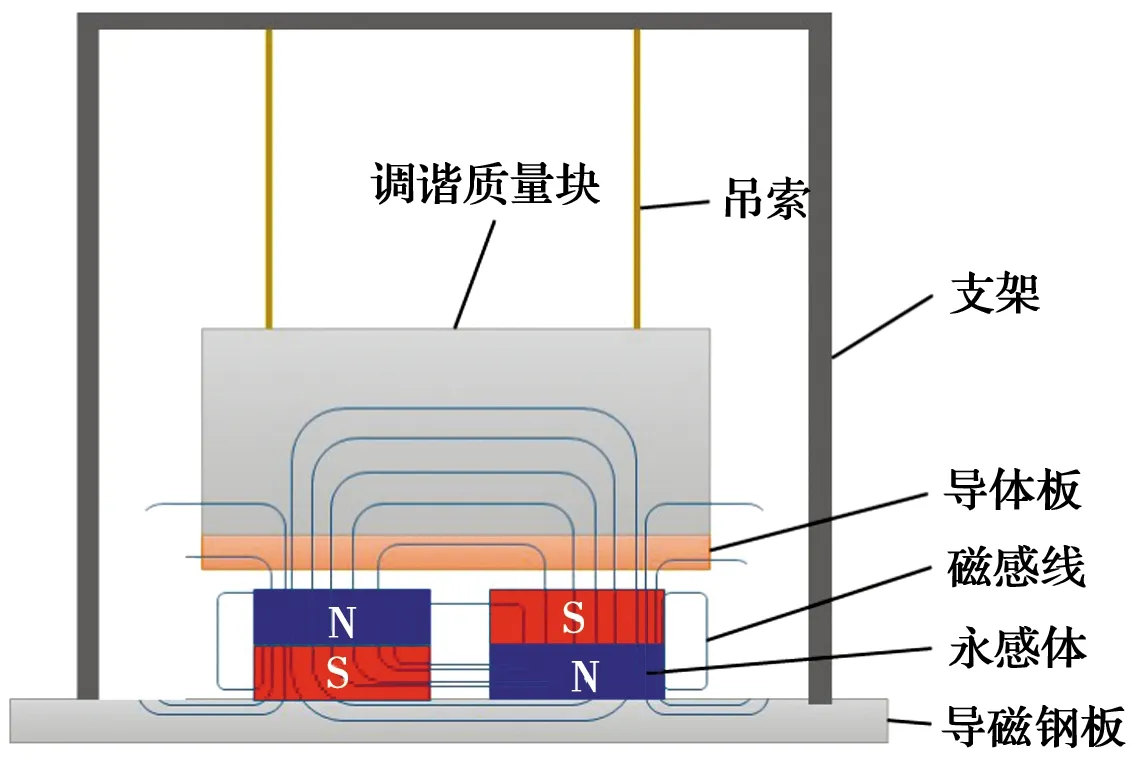
图1 摆式电涡流TMD的组成Fig.1 Composition of pendulum eddy current TMD

当发生地震时，永磁体与导体板(连同调谐质量块)产生相对运动，其切割磁感线的同时产生电磁阻尼力，阻碍其与结构的相对运动，从而减小结构响应。因质量块的运动受到电磁阻尼的阻碍，随即产生电磁能，导体板发热，使地震能量以热能的方式耗散。

2 基于联合仿真的耦合计算方法

由于现有分析软件难以独立完成摆式电涡流TMD与结构相互作用的耦合分析，本文提出一种基于联合仿真的耦合计算方法，将有限元分析软件集成到其他软件平台中，处理该类复杂系统的耦合计算。

2.1 耦合计算方法的建立

以摆式电涡流TMD-钢框架结构模型为例，耦合计算方法采用OpenSEES(Open System for Earthquake Engineering Simulation)作为服务器(server)建立框架结构子系统，并采用Matlab作为客户端(client)建立摆式电涡流TMD子系统，通过socket程序关联，建立起耦合时变系统。耦合计算方法的流程见图2。

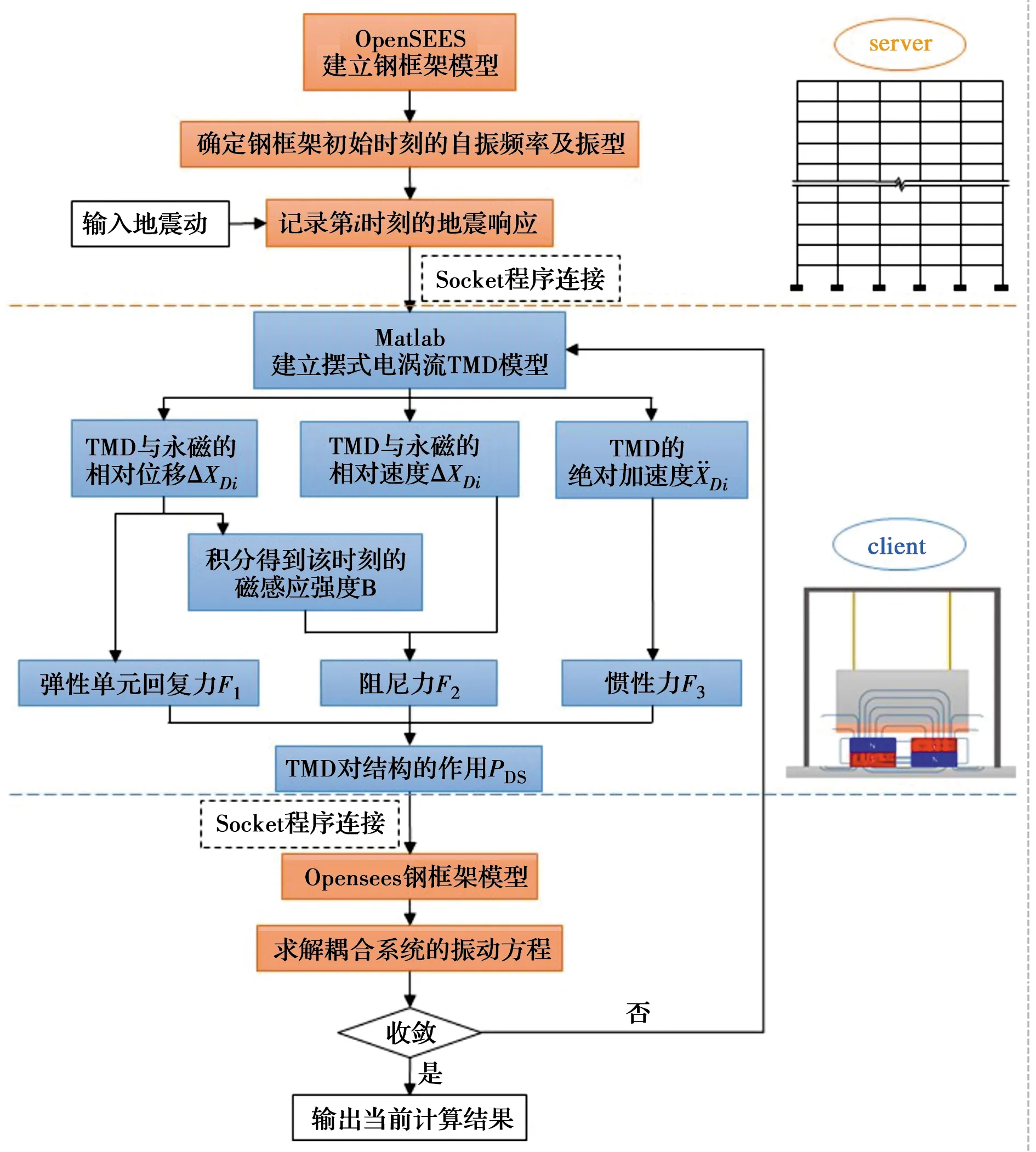
图2 耦合计算方法的流程Fig.2 Flow for coupling calculation method

该耦合时变系统动力学方程可表述为两部分。摆式电涡流TMD子系统为

(1)

钢框架结构子系统为

(2)

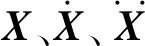
2.2 摆式电涡流TMD的力学模型

采用Matlab建立摆式电涡流TMD的力学模型，包括质量单元、刚度单元、阻尼单元。其中，质量单元和刚度单元简化为单摆模型，如图3所示，其切线方向的力平衡方程为

Fτ=mDaτ=mDgsinφ

(3)

法线方向的力平衡方程为

Fn=mDan=mDgcosφ=mDv2/L

(4)

式中：Fτ为重力的切向分量；Fn为重力的法向分量；mD为摆式电涡流TMD的质量；aτ为切向加速度；φ为摆角；an为法向加速度；v为摆动速度；L为摆长。

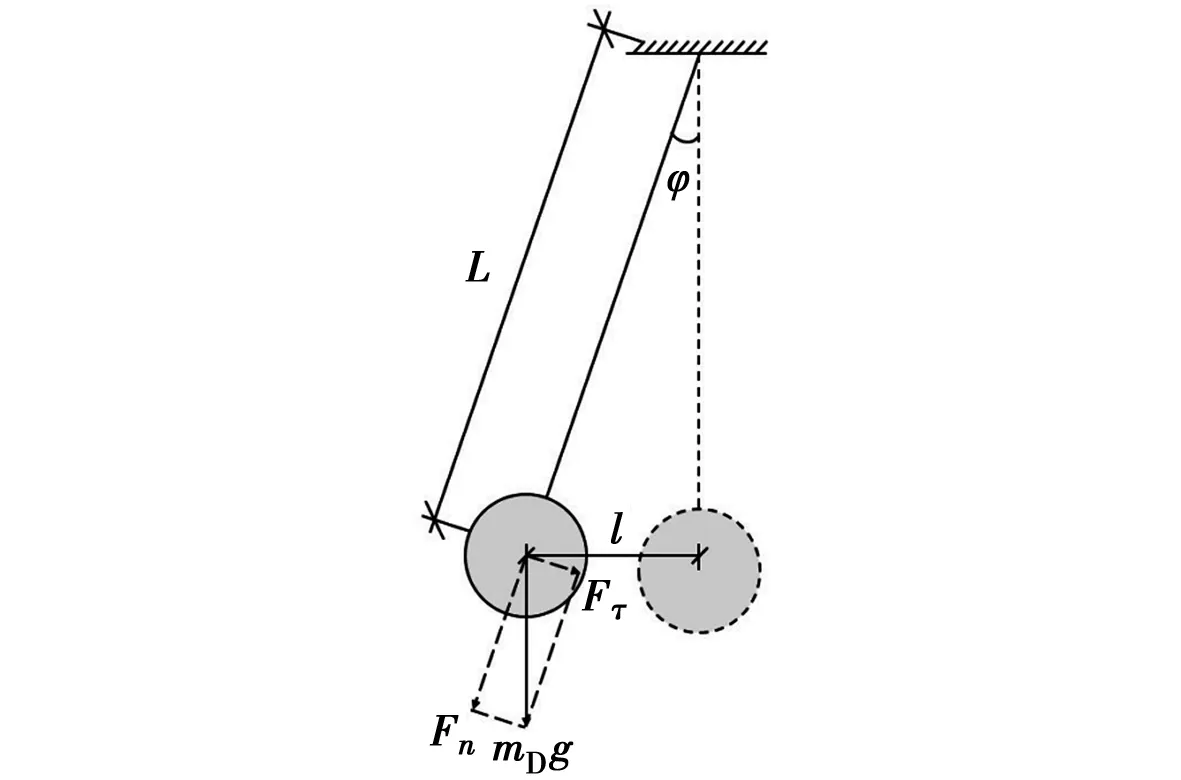
图3 摆式电涡流TMD的计算模型Fig.3 Pendulum eddy current TMD Computational Model

地震过程中φ较小，且刚度单元回复力仅有重力的切向分量，即摆式电涡流TMD的初始刚度kD为

kD=mDgsinφ/l=mDg/L

(5)

式中：l为水平向振幅。

可得摆式电涡流TMD的摆长为

L=g/(2πfD)2

(6)

式中：fD为摆式电涡流TMD自振频率。

摆式电涡流TMD的阻尼由感应电流产生，受磁感应强度B影响，故采用分子电流模型模拟阻尼单元，如图4所示。

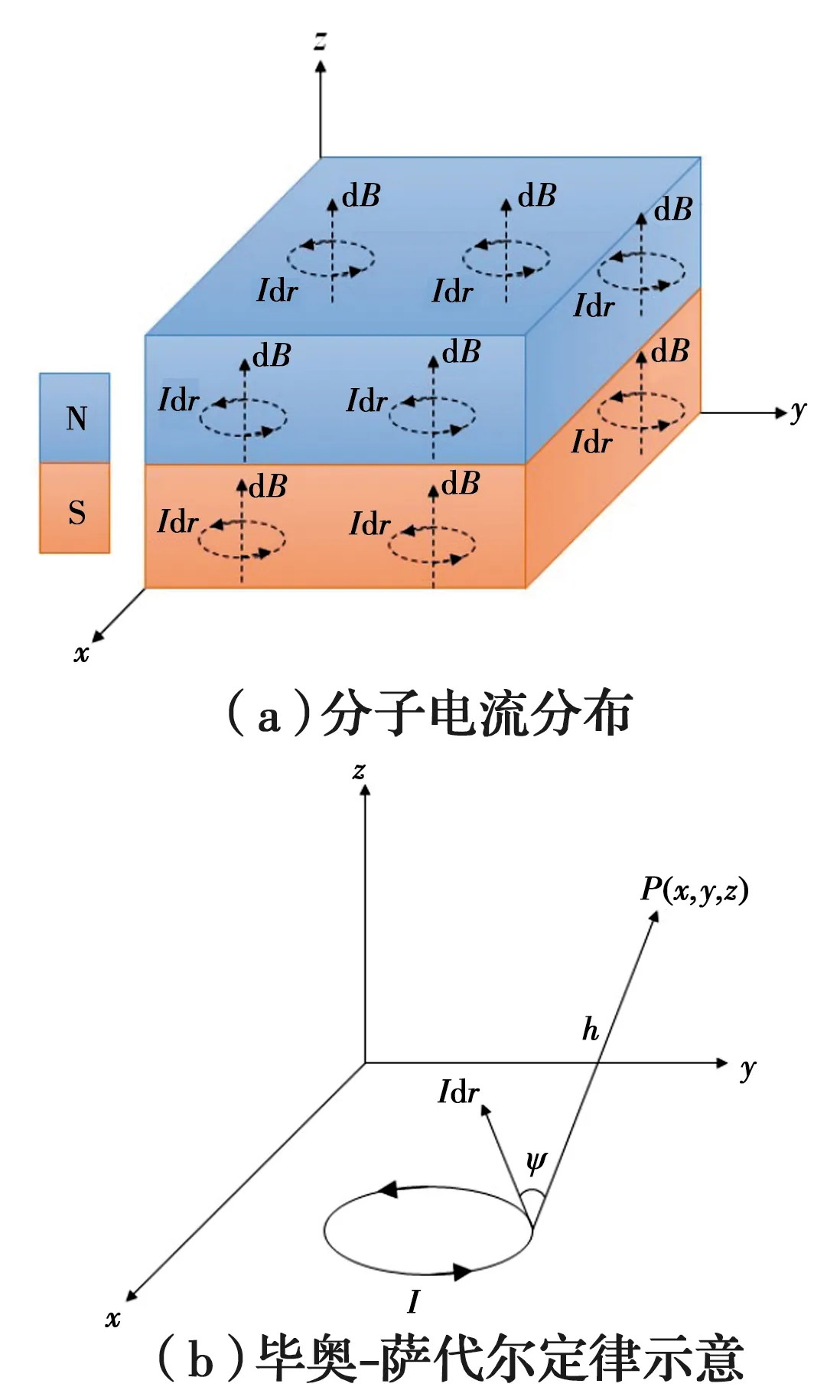
图4 分子电流模型[16]Fig.4 Magnetic induction intensity

在摆动过程中，永磁体与导磁板的间距为

(7)

式中：h0为初始间距。

由毕奥-萨伐尔定律和对永磁体进行体积积分得到导体板处的磁场强度B和摆式电涡流TMD的阻尼系数CD，如式(8)、式(9)所示

(8)

(9)

式中：μ0为空气的导磁率；Idr为永磁体中的环流微元；ψ为环流微元与导磁板任意一点P位置矢量的夹角；σ为导磁板的导电率；V为永磁体体积。

由式(7)～(9)可将CD看作以l为自变量的函数f(l)，在模拟过程中，通过socket程序向OpenSEES发送指令并求得l，利用分子电流模型结合毕奥-萨伐尔定律计算出导体板处的B，最后积分得到摆式电涡流TMD的CD。至此，可得到摆式电涡流TMD的质量单元、刚度单元、阻尼单元，并可在Matlab中建立摆式电涡流TMD子系统。

3 结构模型设计及地震动记录选取

3.1 结构模型的建立

采用OpenSEES建立5、10、20层单榀钢框架结构模型，结构顶层放置摆式电涡流TMD。钢框架结构的抗震设防烈度为8度(0.2g)，场地类别为ΙΙ类，设计地震分组为第2组。柱截面采用HW428×407×20×35，梁截面采用HN500×200×10×16。3个结构模型的第1自振周期T1为分别为0.55、1.08、2.18 s。各楼层的恒荷载和活荷载分别为23.53、6.60 kN/m，屋面的恒荷载和活荷载分别为14.85、6.60 kN/m，如图5所示。

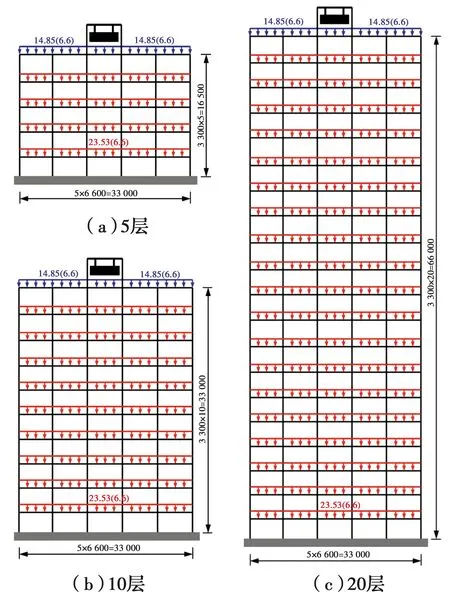
图5 结构模型及荷载分布Fig.5 Structural model and load distribution

材料采用Q345钢，由Steel 01单元模拟。梁柱由Displacement-Based Beam-Column单元模拟，阻尼比为3%，采用Rayleigh阻尼。结构进行时程分析时，仅考虑水平地震作用。

3.2 摆式电涡流TMD参数设计

在摆式电涡流TMD的设计中，质量为控制指标，通过简化摆式电涡流TMD-钢框架结构模型，得到频率比、阻尼比与质量比的关系，如图6所示。

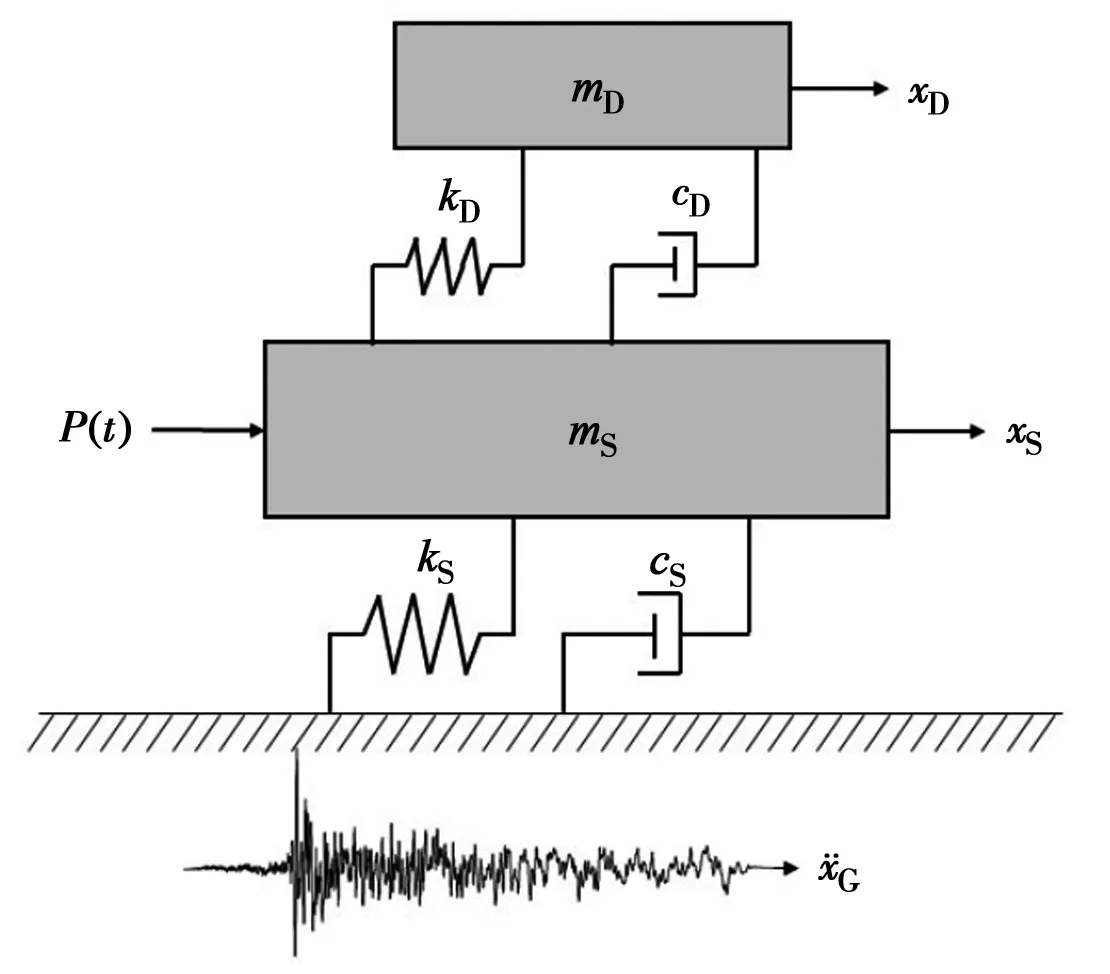
图6 摆式电涡流TMD-钢框架计算模型Fig.6 SDOF structure and TMD computational model

摆式电涡流TMD-钢框架的运动方程为

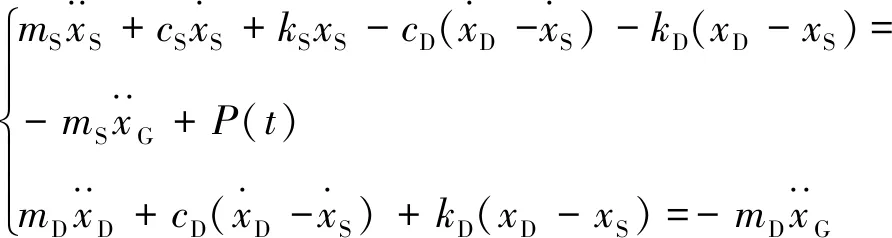
(10)

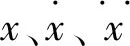
通过上述方程可求得xS及地震作用P(t)的频谱特性G(jω)，用S0表示P(t)的频谱密度，根据G(jω)求得钢框架结构位移xS的频谱密度，表示为S1(ω)，最后计算出钢框架结构的振动位移方差为

(11)

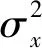
(12)

(13)

式中：μf为摆式电涡流TMD振动频率与钢框架结构一阶自振频率之比；μm为摆式电涡流TMD质量与钢框架结构质量之比；μξ为摆式电涡流TMD提供的附加阻尼比。

根据式(12)和式(13)分别设计了5组摆式电涡流TMD模型，具体参数如表1所示。

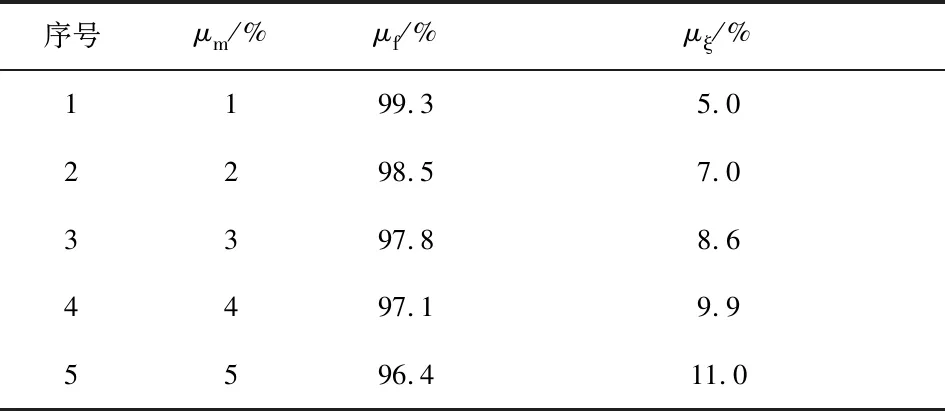
表1 摆式电涡流TMD参数Table 1 Design parameters of pendulum eddy current TMD

3.3 地震动记录的选取

按照《建筑结构抗震设计规范》(GB 50011—2010)中有关地震动选取的要求，从太平洋地震工程研究中心地震波数据库中选取了11条实际记录，相关参数见表2，其加速度反应谱与规范反应谱的对比如图7所示。由图7可以看出，平均反应谱分别在3个结构的T1处与设计反应谱可较好地吻合。

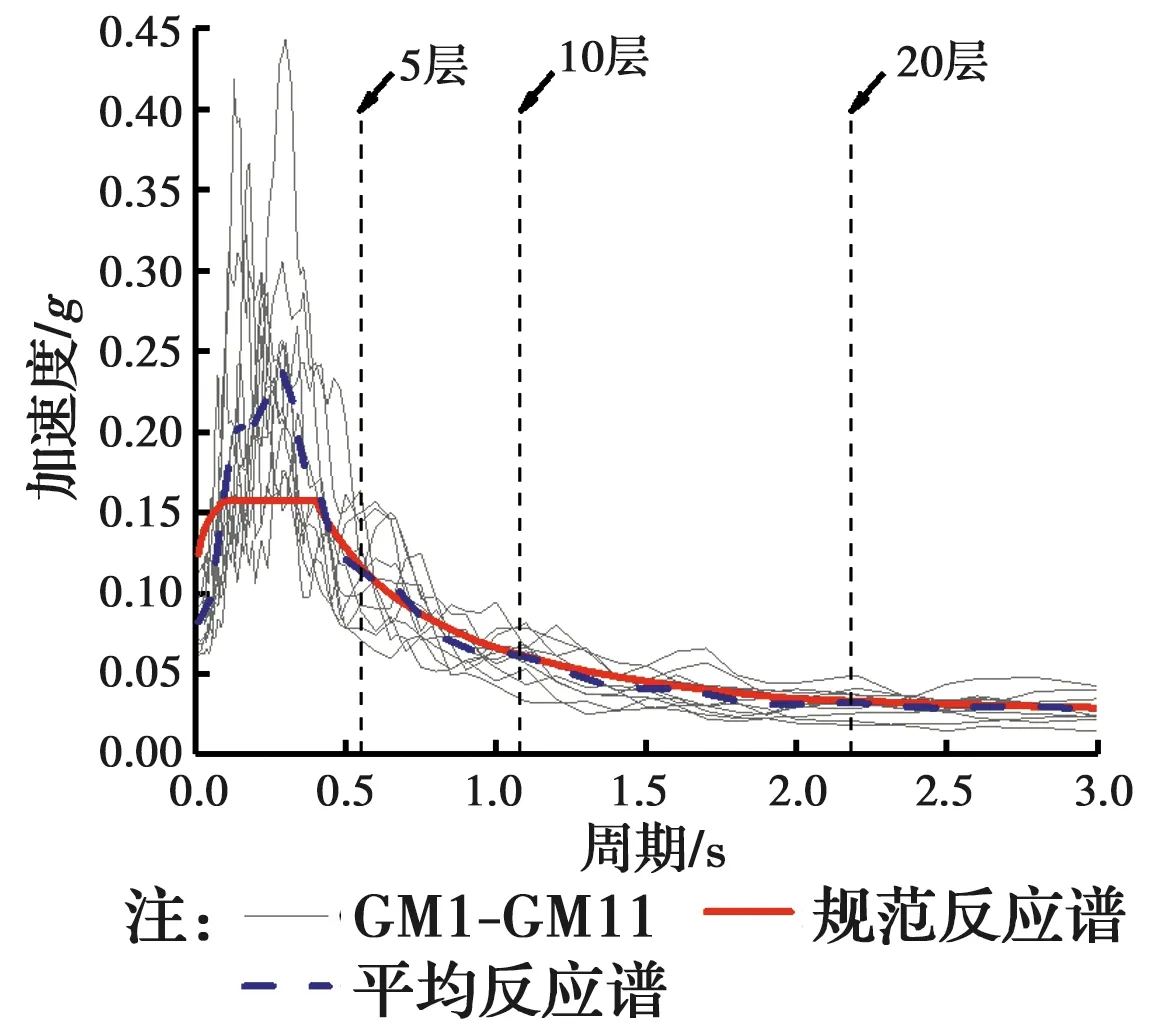
图7 加速度反应谱对比Fig.7 Comparison of response spectra

4 结构减震性能分析

将所选的11条地震动基于PGA调幅到《建筑结构抗震设计规范》(GB 50011—2010)中规定的罕遇地震加速度最大值，并分别对5、10、20层摆式电涡流TMD-钢框架结构进行动力时程分析，以得到不同质量比μm的结构地震响应。

表2 地震动记录参数Table 2 Parameters of ground motion records

4.1 层位移和层间位移角

将不同μm、不同层数结构在罕遇地震作用下的层位移和层间位移角进行对比，如图8和图9所示。比较5、10、20层结构的时程分析结果可知，最大位移均出现在结构顶层，最大层间位移角均出现在各结构的中低部，且在不同质量比下的变化趋势相似，说明摆式电涡流TMD的设置并未改变框架结构剪切变形的特点。同时，结构在设置摆式电涡流TMD后，其位移响应显著降低。

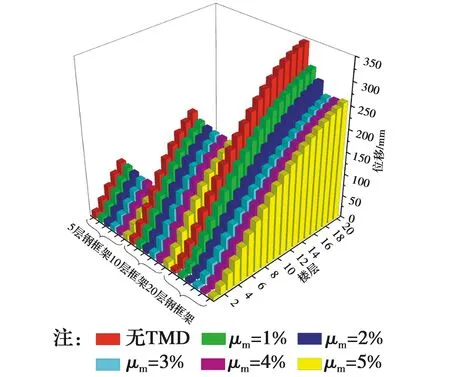
图8 不同质量比下的层位移Fig.8 Story drift under different mass ratios

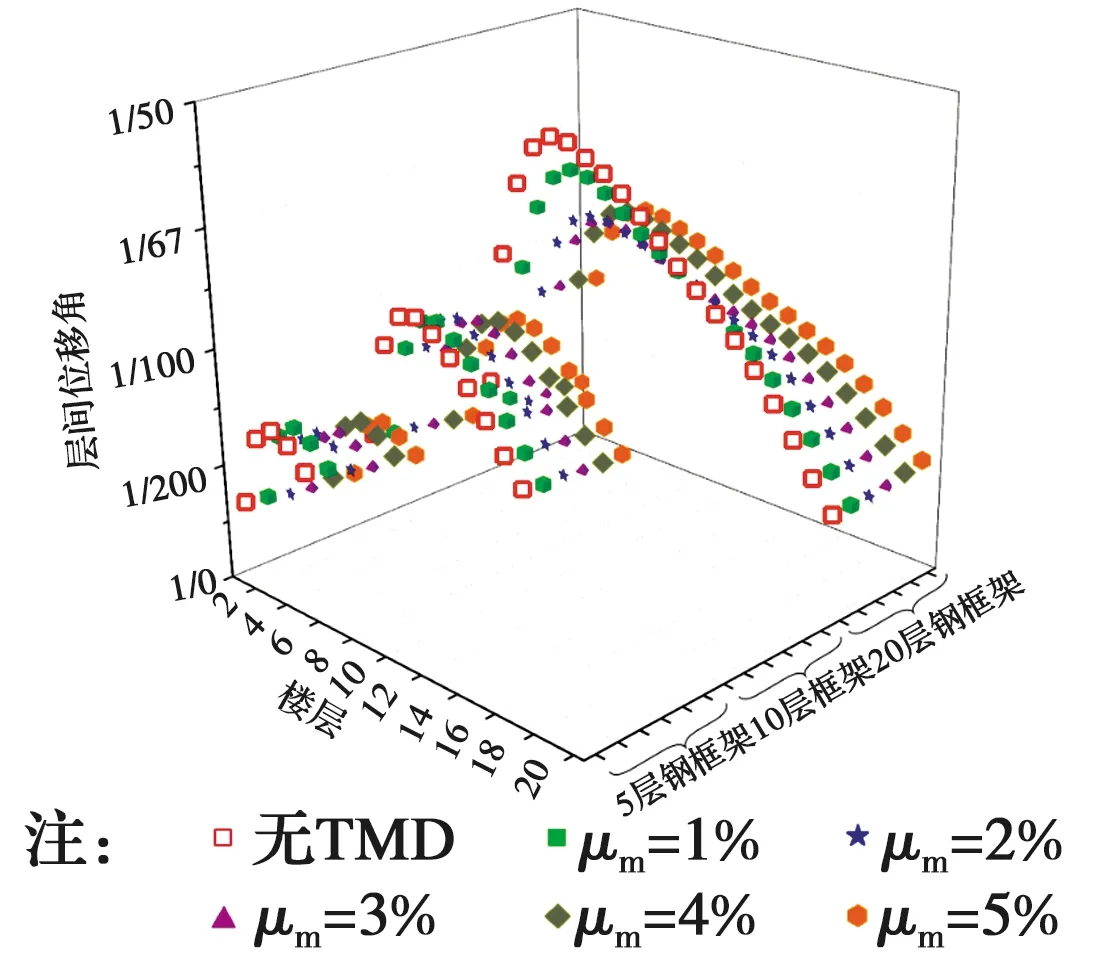
图9 不同质量比下的层间位移角Fig.9 Interstory drift ratio under different mass ratios

顶层位移和最大层间位移角见表3。由表3可知，当μm为1%时，结构顶层位移分别减小2.0%、6.3%、13.2%，最大层间位移角分别减小3.4%、4.9%、9.0%，随着μm继续增大，顶层位移减小率分别维持在10.2%、11.0%、25.9%左右，最大层间位移角减小率分别维持在17.5%、20.7%、27.4%左右。总体来看，结构高度越高，减震效果越明显。其中，当结构层数为20层时，μm为3%时的顶层位移相较于μm为1%时减小15.2%，但μm为5%时的顶层位移相较于μm为3%时反而增大了1.6%，这是由于μm的增大引起了水平地震作用的增大，且摆式电涡流TMD设置在结构顶层，鞭梢效应进一步增大了结构的位移响应，导致其减震效果并未随着μm的增大而发生明显变化，由此可见μm并非越大越好。

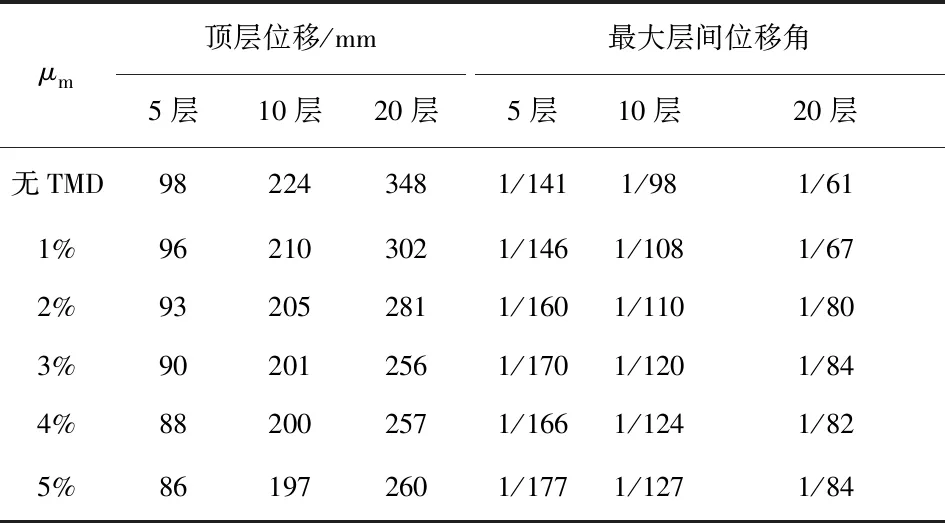
表3 顶层位移和最大层间位移角Table 3 Top story drift and maximum interstory drift ratios

4.2 层剪力

将不同μm、不同层数结构在罕遇地震作用下的层剪力进行对比，如图10所示。由图10可知，当结构高度较低时，摆式电涡流TMD对层剪力的减震效果并不明显，随着结构高度的增加，减震效果逐渐明显。这是由于摆式电涡流TMD的电磁阻尼力需要通过永磁体与导体板(连同调谐质量块)的相对运动产生，其相对运动又是由结构响应导致的。换言之，结构响应越大，相对运动越显著，产生的电磁阻尼力也就越大。因此，楼层数较少的结构相较于楼层数较多的结构，其层剪力的减震效果也就越不明显。随着μm的增加，各结构的减震效果逐渐增大。其中，当结构层数为20层时，μm为3%时的顶层剪力相较于μm为1%时减小了2.7%，而μm为5%时的顶层剪力相较于μm=3%时仅减小1.7%，也进一步验证了前面的结论。同时，当以层剪力为减震指标时，需考虑摆式电涡流TMD的质量过大带来的影响。

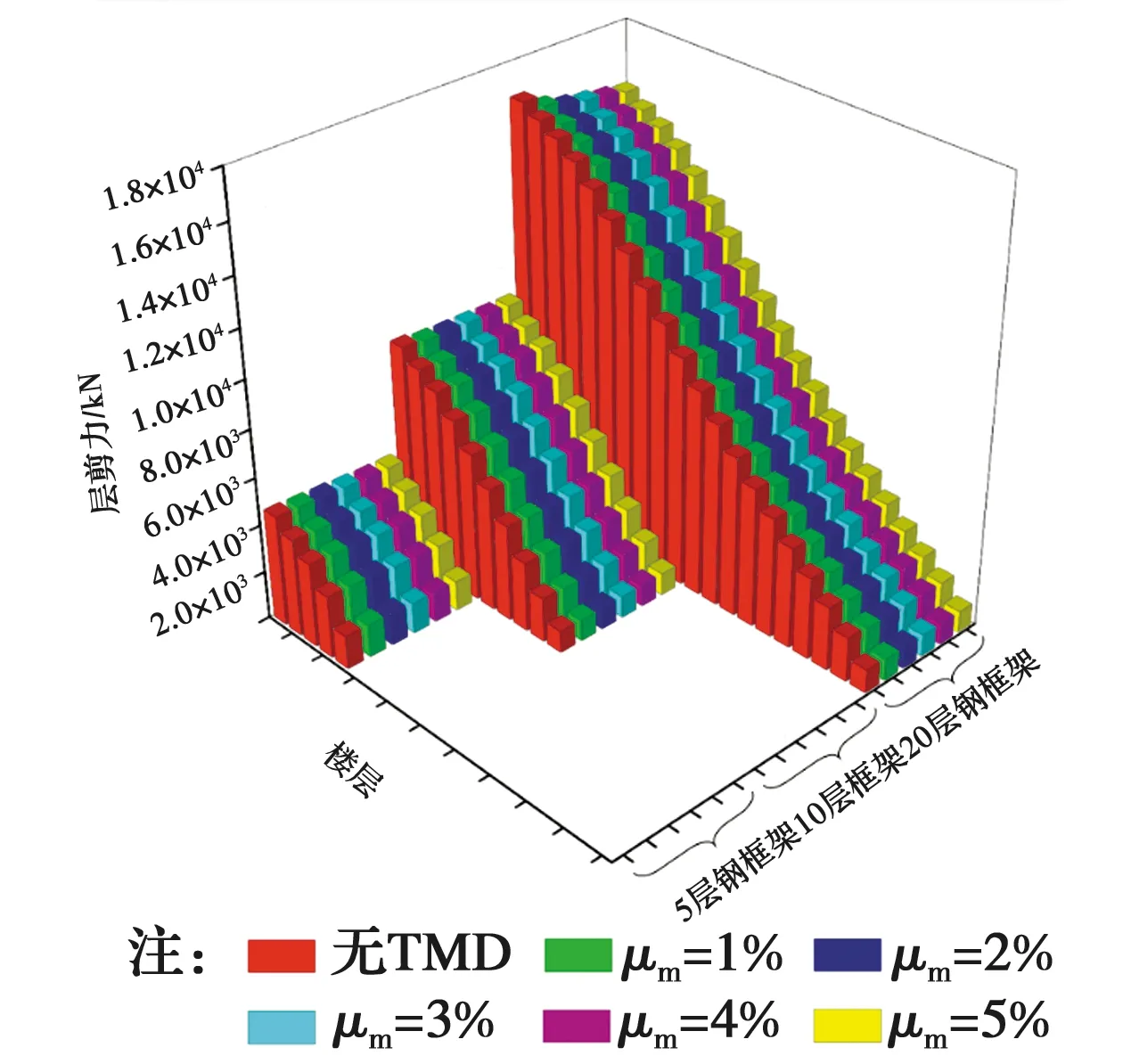
图10 不同质量比下的层剪力Fig.10 Story shear under different mass ratios

不同μm下的基底剪力见表4。由表4可知，μm=1%时，基底剪力分别减小0.7%、1.3%、2.8%，但μm大于3%后，基底剪力减小率维持在3.7%、2.2%、6.0%左右，减小趋势不明显。这也是由于水平地震作用的增大和鞭梢效应的共同作用，导致了μm的增大对层剪力的减震效果并不明显。

4.3 层加速度

不同μm、不同层数结构的层加速度对比见图11。由图11可知，最大加速度均出现在结构顶层。其中，无摆式电涡流TMD的结构层加速度最大，说明摆式电涡流TMD能够控制结构加速度响应，且随着μm的增大，加速度响应逐渐减小，但对比层位移和层间位移角，其对于加速度的减震效果并不明显。将同一μm、不同层数结构在罕遇地震作用下的层加速度变化趋势进行对比可知，随着楼层数的增加，结构高阶振型的质量参与系数逐渐增大，导致楼层数较多的结构相较于楼层数较少的结构，其加速度并非逐层增加。但基于结构一阶振型设计的摆式电涡流TMD仍能对各个振型的加速度加以控制，使结构的层加速度响应变化趋势与原结构仍保持一致，并随着μm的增大逐渐减小。

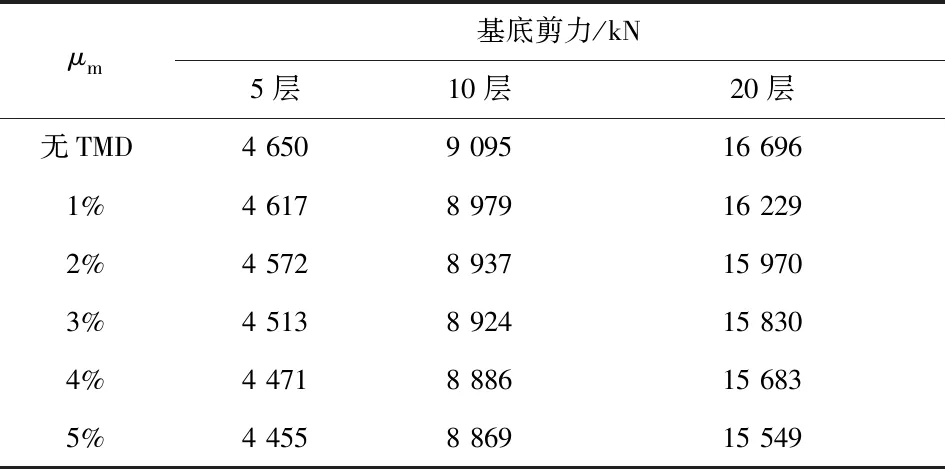
表4 不同质量比下的基底剪力Table 4 Base shear force under different mass ratios

4.4 减震率

为定量分析摆式电涡流TMD的减震性能，得出μm的合理取值范围，提出了公式(14)。

(14)

式中：ζj为减震率；j为不同的地震响应指标(d为层位移，θ为层间位移角，s为层剪力，a为层加速度)；i为楼层；n为总楼层数；R为无摆式电涡流TMD时的结构地震响应；r为设置摆式电涡流TMD后的结构地震响应。

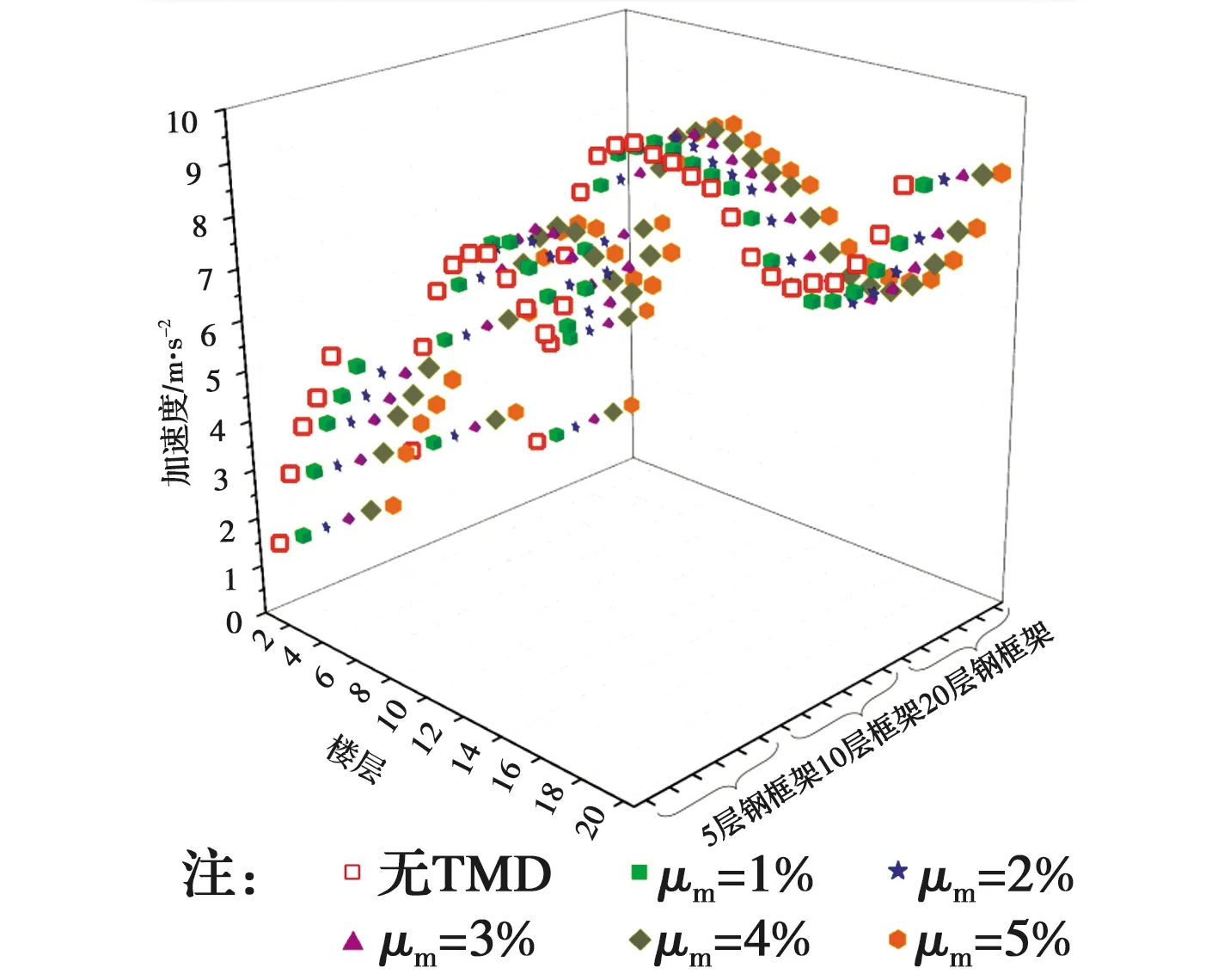
图11 不同质量比下的层加速度Fig.11 Story acceleration under different mass ratios

以20层钢框架结构为对象，按式(14)，分别对层位移、层间位移角、层剪力、层加速度等4个指标分别进行减震率计算，见表5。由表5可知，摆式电涡流TMD对层位移和层间位移角的减震效果最好，对层剪力和层加速度的减震效果较差。其中，ζd的平均值在22.4%左右，ζθ的平均值在17.8%左右。

表5 不同质量比下20层结构的减震率Table 5 Seismic reduction ratio of twenty story structure under different mass ratios %

从图12可知，当μm小于3%时，20层结构的各减震率随着μm的增大而逐渐增大，且上升趋势明显。但在μm大于3%后，ζs和ζa增长放缓，而ζd和ζθ的减震率呈下降趋势，这说明摆式电涡流TMD的减震性能随着μm的增大而趋于平缓，甚至降低。这是因为摆式电涡流TMD在地震作用下的响应存在滞后性，同时质量的增加会带来水平地震作用的增加以及鞭梢效应的加重，引起结构的地震响应更加剧烈，降低了摆式电涡流TMD的减震效果。

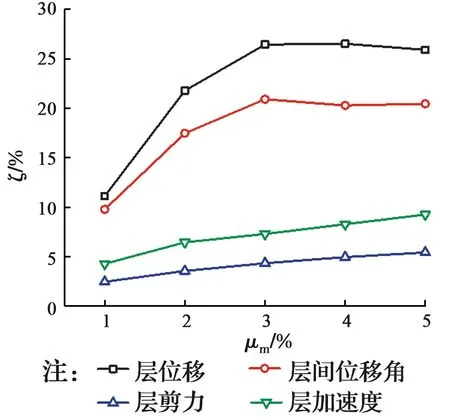
图12 20层结构的减震率-质量比关系曲线Fig.12 Relationship of Seismic reduction ratio and mass ratios of twenty story structure

5 结论

为研究摆式电涡流TMD对建筑结构的减震性能，提出了基于联合仿真的耦合计算方法，建立了5、10、20层钢框架结构模型，选取了11条地震动记录，比较了不同质量比的摆式电涡流TMD-钢框架结构在罕遇地震作用下的响应，得到以下结论：

1)基于联合仿真的耦合计算方法既能模拟钢框架结构在地震作用下的响应，又能模拟摆式电涡流TMD阻尼的时变过程，且计算流程简单直观，能够用于摆式电涡流TMD与钢框架结构的减震分析。

2)通过减震分析，摆式电涡流TMD能够减小钢框架结构的地震响应，结构越高，减震效果越好，且合理质量比建议为3%。其中，20层钢框架结构的层位移、层间位移角、层剪力和层加速度分别减小了26.5%、20.9%、4.3%、7.3%。摆式电涡流TMD对钢框架结构层位移和层间位移角的减震效果较好。

3)当质量比小于3%时，各指标的减震率随着质量比的增大而明显增加；当质量比大于3%后，虽层剪力和层加速度的减震率会随着质量比的增大而略微增大，但层位移和层间位移角的减震率会明显减小。建议在摆式电涡流TMD的减震设计过程中，宜根据减震指标的不同，选择合适的质量比。