粘贴铝合金板加固钢筋混凝土梁的界面剪应力

2020-08-24杨立军邓志恒梁朋杨海峰

土木与环境工程学报 2020年4期

杨立军，邓志恒，梁朋，杨海峰

(1.洞庭湖生态经济区建设与发展省级协同创新中心，湖南常德 415000；2.湖南文理学院土木建筑工程学院，湖南常德 415000；3.广西大学土木建筑工程学院，南宁 530004；4.德成建设集团有限公司,湖南常德,415000)

铝合金材料具有良好的力学性能：较高的强质比(是普通钢材的3倍)，不腐蚀，较好的变形性能，力学性能低温不敏感，具有特殊的光泽与质感，在工程中应用广泛[1-2]，尤其适合沿海侵蚀环境、潮湿、低温和高寒等极端环境混凝土结构的加固[3]。目前钢板和FRP作为钢筋混凝土(Reinforce Concrete，RC)结构的加固材料得到了充分的研究[4-6]，但钢板容易腐蚀，腐蚀后力学性能退化；FRP是脆性材料，破坏前没有明显的征兆。由于铝合金相对于这两种材料具有明显的优点，是一种理想的RC结构加固材料，开始吸引了研究者的兴趣。

目前，对铝合金加固RC梁的研究集中在抗剪、抗弯性能及破坏模式方面。Abdalla等[7]完成了不同方向铝合金板加固RC梁的抗剪试验，发现其抗剪承载能力可比未加固梁提高24%～89%；Obeidah[8]和Abu-Obeidah等[9]研究了不同形状与不同方向外粘铝板加固RC梁的抗剪性能，发现铝合金板加固RC梁的抗剪承载能力比基准梁提高10%～89%，并在此试验基础上，完成了三维非线性有限元模型开发，可用于铝合金板加固RC梁的抗剪性能预测；Rasheed等[10]完成了外粘铝板加固RC梁的抗弯承载能力试验研究，发现在端部锚固条件下，RC梁抗弯承载能力提高的同时，其延性相比CFRP加固梁提高13%到40%左右；Xing等[11]以纵向配筋率及混凝土强度为主要变量，完成了11根铝合金筋体加固混凝土梁的抗弯试验研究；柳红滨[12]基于板端钢筋是由于板端弯矩和板端裂缝间界面剪应力共同作用下屈服的假设，建立了板端弯剪破坏的破坏准则和计算公式，对铝合金加固RC梁破坏模式开展了理论与试验研究；宋启玺[13]通过对铝合金筋体外预应力加固RC梁的理论研究和有限元模拟后发现，用同等强度的铝合金加固RC梁，加固梁的承载能力得到较大幅度提高的同时，加固梁的延性也会得到了相应的提高。以上研究表明铝合金加固RC梁在提高RC梁的承载力同时具有很好的延性。铝合金与RC梁的粘贴界面力学行为关乎两种材料是否能协同工作，是铝合金板加固RC梁可靠工作的关键因素。这方面的研究目前未有报导，虽然杨立军等[14-15]通过铝合金板和混凝土块体的面内单剪试验对其粘结性能和粘结强度开展了研究，但因为其单向受力状态不同于铝合金板加固RC梁的弯剪复合受力状态，其成果仅能作为铝合金板加固RC梁粘贴界面力学行为的工作基础。

笔者通过铝合金板纵轴线上密布应变片的铝合金板加固RC梁简支梁三分点加载试验，得到了铝合金板与RC梁的粘贴界面剪应力；推导了一般荷载作用下的无附加锚固铝合金板加固RC梁的粘贴界面剪应力的通解，得到了常见荷载作用下的粘贴界面剪应力解析表达式和最大值。结合理论和试验研究结果，分析了铝合金板与RC梁的粘贴界面剪应力分布规律，为铝合金板加固RC梁的工程应用提供了依据。

1 界面剪应力的理论研究

1.1 一般荷载作用下的界面剪应力的通解

如图1所示铝合金板加固RC梁，铝合金板与RC梁通过满布的结构胶粘贴连接，没有设置附加锚固。设梁上作用任意分布力q(x)，跨度l，RC梁宽为b，高为h，形心轴与底边距离y0，铝合金板板端与支座距离l0。设RC梁截面形心轴为x轴，y轴通过铝合金板板端。

图1 铝合金板加固RC梁Fig.1 RC beam strengthened with AAP

设结构胶界面剪应力τ(x)，由图2所示微元体，有

(1)

(2)

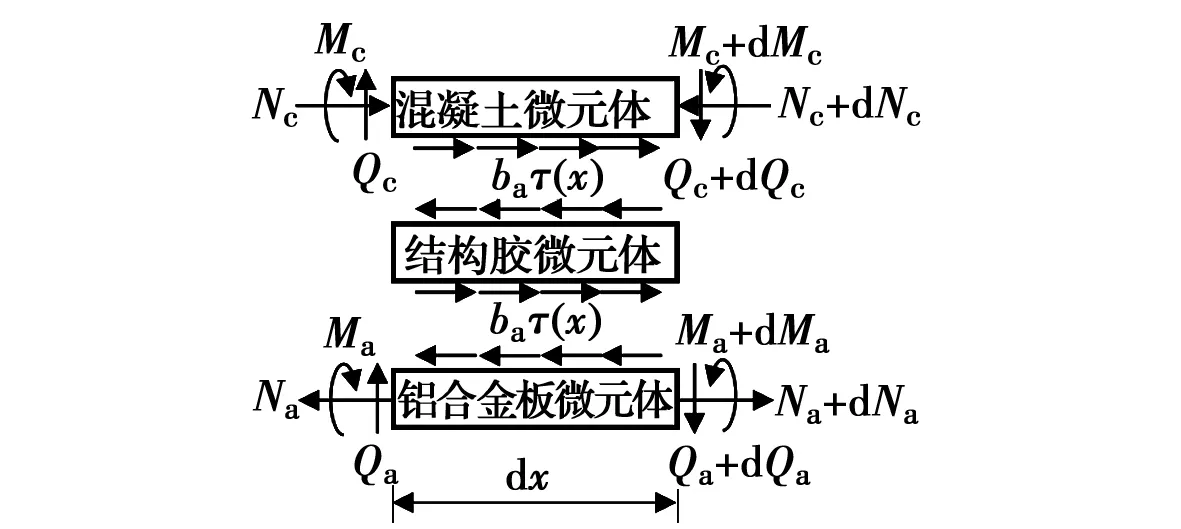
图2 微元体Fig.2 The small elements

设结构胶水平位移up，由于位移协调，上界面处水平位移为RC梁底面水平位移uc，下界面处水平位移为铝合金板上表面水平位移ua。考虑到结构胶厚度很小，设剪切变形沿厚度tp线性变化，则结构胶剪应变γp为

(3)

结构胶上、下界面处水平位移uc和ua分别为

(4)

式中：Ec、Ic和Ac分别为RC梁弹性模量、截面惯性矩和面积；Ea、Ia和Aa分别为铝合金板的弹性模量、截面惯性矩和面积。

设结构胶剪切模量为Gp，在剥离破坏前剪应力-剪应变关系符合胡克定律[16]，即

τ(x)=Gpγp

(5)

铝合金板厚度相对于RC梁高很小，相应的惯性矩相对更小，其承担的弯矩远小于RC梁，设所有弯矩M(x)由RC梁承担，即有Ma(x)=0，Mc(x)=M(x)。这样，对式(5)求导，结合式(3)和式(4)，有

(6)

再次对式(6)求导，并将式(1)～式(2)代入，可得

(7)

式(7)即为界面剪应力τ(x)的控制方程，其解为

τ(x)=C1cosh(γx)+C2sinh(γx)+τ1(x)

(8)

式(8)中：C1、C2为积分常数，由边界条件确定，τ1(x)是对应于-λQ(x)项的特解。

式(8)即为任意分布力q(x)作用下的无附加锚固铝合金板加固RC梁的界面剪应力τ(x)的通解。

1.2 常见荷载作用下的界面剪应力理论解

现在推导四集中荷载作用的铝合金板加固RC梁界面剪应力的理论解，如图3所示。梁的剪力方程Q(x)为

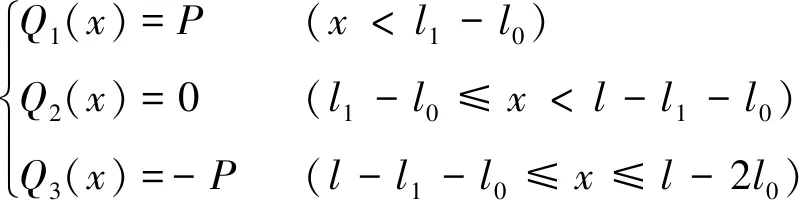
(9)

将式(9)代入式(8)，得到四集中荷载作用下的铝合金板加固RC梁的界面剪应力解为

(10)

图3 四集中荷载作用的铝合金板加固RC梁Fig.3 RC beam strengthened with AAP under four concentrated loads

当x=0时，Na=Nc=0，由式(6)可以得到

(11)

由梁的对称性，有

当x=0.5l-l0时，τ″(x)=0

(12)

根据界面剪应力τ(x)连续性条件，有

τ′(l1-l0)=τ″(l1-l0)，

τ″(l-l1-l0)=τ‴(l-l1-l0)，

(13)

这样，由6个边界条件得到6个方程，可以求出6个积分参数C1～C6为

(14a)

C3=-C4tanh[γ(0.5l-l0)]

(14b)

C1=C3+C4coth[γ(l1-l0)]-C2coth[γ(l1-l0)]

(14c)

(14d)

C5=C3+C4coth[γ(l-l1-l0)]-

C6coth[γ(l-l1-l0)]

(14e)

将积分常数C1～C6的值代入式(10)，即可得到四集中荷载作用的铝合金板粘贴界面的剪应力τ(x)的解析式。当l1=l/3时，即为简支梁三分点加载时铝合金板粘贴界面的剪应力τ(x)的解析式。

最大界面剪应力τmax在x=0即铝合金板板端取得，其表达式为

(15)

同样，由式(8)可以求得其他荷载作用时的铝合金板加固RC梁的界面剪应力的解析解。

当如图3所示铝合金板加固RC梁作用均布荷载q时，界面应力理论解τ(x)和最大界面剪应力τmax为

τ(x)=D1cosh(γx)+D2sinh(γx)+

(16)

(17)

当如图3所示铝合金板加固RC梁跨中作用集中荷载P1时，界面应力理论解τ(x)和最大界面剪应力τmax为

(18)

(19)

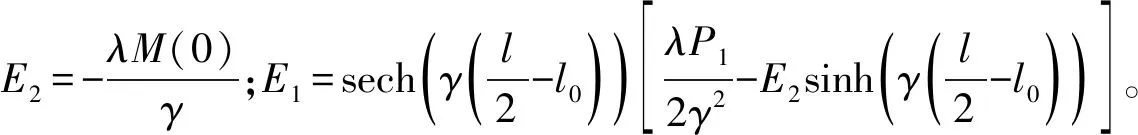
2 界面剪应力的试验研究

2.1 试验设计

以三分点加载的铝合金板加固RC梁来验证界面剪应力理论解，铝合金板加固RC梁示意图如图4所示，试验梁净跨2 700 mm，梁宽b×梁高h=200 mm ×300 mm。通过工字钢分配梁对试验梁三分点进行加载，形成了长900 mm的纯弯段BC和剪弯段AB、CD。箍筋和架立筋采用HPB300级钢筋，架立筋28，纯弯段箍筋8@180，剪弯段箍筋8@100；梁底配置纵筋212，HRB400级钢筋。混凝土设计强度等级为C35。RC梁端部附近区域弯矩较小，仅在纯弯段及纯弯段附近550 mm区域内贴板加固，为了贴板方便，铝合金板宽度稍小于RC梁宽度，取铝合金板长度la×宽度ba为2 000 mm×180 mm，厚度ta有2 mm，4 mm和6 mm 3种规格，型号为6061-T6。

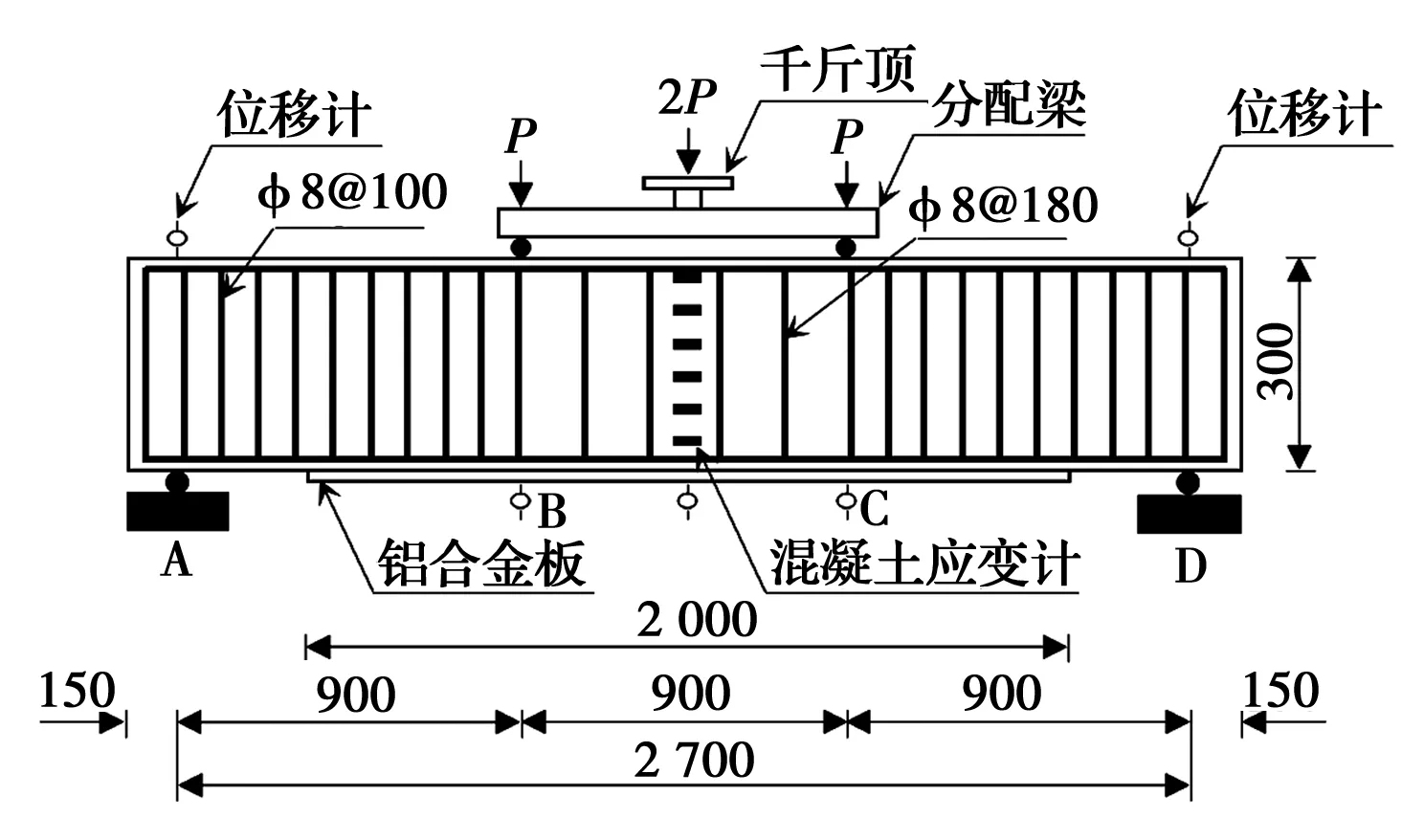
图4 试验梁示意图Fig.4 Schematic diagram of test beams

为便于粘贴铝合金板，翻转RC梁使受拉底面朝上。对铝合金板和混凝土粘贴界面进行打磨糙化、吹风机吹尘和乙醇清洗，粘贴界面自然干糙后在RC梁底面对称均匀抹涂3 mm厚JN建筑结构胶，粘贴铝合金板时均匀压紧铝合金板，使结构胶缓缓均匀从板的边缘挤出，此后在铝合金板上均匀平铺重物，直至结构胶达到设计强度后卸去重物。部分铝合金板加固RC梁在结构胶粘贴的基础上，在板端或梁的三分点处(即B、C位置)设置了铝合金U形箍附加锚固，U形箍由宽50 mm厚5 mm的5052-T6铝合金板冷弯而成，U形箍内侧均匀抹涂3 mm厚JN建筑结构胶后固定在RC梁预定位置，U形箍顶部采用M12化学螺栓固定在RC梁侧面，化学螺栓钻入混凝土80 mm，如图5所示。用U0、U1和U2区分U形箍设置情况：U0表示没有设置U形箍，U1表示仅在铝合金板板端设置U形箍，U2表示在铝合金板板端和梁的三分点处均设置U形箍。

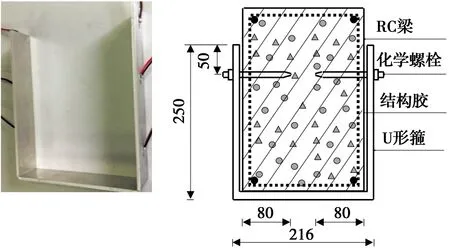
图5 U形箍和U形箍连接Fig.5 U-wraps and its connection

混凝土采用南宁华润西乡塘混凝土有限公司生产的商品混凝土，浇筑RC试验梁同时浇筑了3个150 mm×150 mm×150 mm混凝土立方体标准试块，试块与RC梁在同样环境下养护28 d后，按照《普通混凝土力学性能试验方法标准》(GB/T 50081—2016)采用华龙混凝土压力试验机对混凝土立方体同养试块进行了抗压试验，测得立方体抗压强度为41.3 MPa；铝合金材料从深圳市宝安区西乡鑫锦发铜铝材料行购买，力学性能如表1所示。表1中，Ea为弹性模量，f0.1(f0.2)为残余应变0.1%(0.2%)时的应力，fau为与极限应变εau对应的极限强度，n为反映材料应变硬化的参数。JN建筑结构胶由湖南固特邦土木技术发展有限公司生产，力学性能如表2所示。表2中，fpt、fpm和fpc分别为抗拉强度、抗弯强度和抗压强度，Ep为弹性模量，εpu为伸长率。钢筋为柳州钢铁股份有限公司生产，力学性能如表3所示。表3中，fy和fu分别为钢筋的屈服强度和极限强度，εy、εsu和Es分别为钢筋的屈服应变、极限应变和弹性模量。

表1 铝合金板力学性能Table 1 Mechanical properties of aluminium alloy plates

表2 结构胶力学性能Table 2 Mechanical properties of structural adhesive

表3 钢筋力学性能Table 3 Mechanical properties of steel bars

考虑铝合金板厚度和U形箍设置方式等因素，设计了6根铝合金板加固RC梁，试验梁的参数如表4所示。

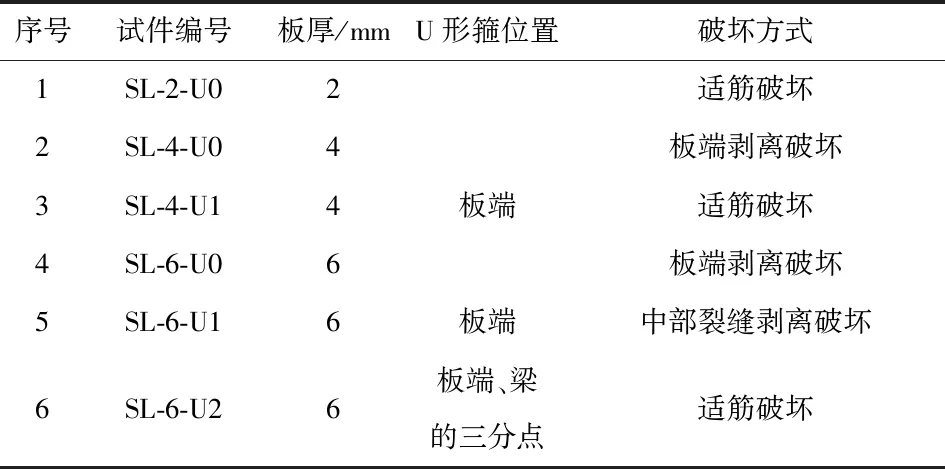
表4 试验梁的参数Table 4 Parameters of test beams

液压千斤顶以5 kN为一级对试验梁施加单调静力荷载，每级荷载持荷5 min，直到试件破坏，加载图如图6所示。试件破坏的标准为：1)RC梁最大裂缝宽度达到1.5 mm，或挠度达到跨度的1/50；2)受压区混凝土压碎；3)铝合金板与RC梁剥离。

图6 试验梁加载图Fig.6 Drawing of test beams under loading

2.2 测点布置

在混凝土梁跨中侧面沿高度方向布置6个混凝土应变片；试验梁支座、跨中和纯弯段端点布置位移计，二者布置示意图如图4所示。U形箍两个侧面各布置3个应变片，如图5所示。主筋在纯弯段三分点处各设置一个应变片，纯弯段端点处箍筋中部布置一个应变片，如图7所示。

图7 钢筋应变片布置Fig.7 Arrangement of strain gauges of bars

液压千斤顶和反力板之间放置压力式荷重传感器测试荷载大小。铝合金板纵轴线上每相距50 mm布置一个应变片，从左到右编号分别为A1～A39，应变片布置如图8所示(图中只画出了对称的左半部分)。荷载、应变传感器等信号通过DH3821测试分析系统实时采集，存储在计算机中。

图8 铝合金板应变片布置示意图Fig.8 AAP strain gauges arrangement diagram

2.3 试验结果

如表4所示，试验梁的破坏方式有：钢筋和铝合金板屈服后混凝土压碎——适筋破坏；铝合金板板端剥离破坏；中部裂缝剥离破坏。3种破坏的照片如图9所示。适筋破坏是延性破坏，后两种破坏统称为剥离破坏，属于早期破坏，具有突然性，是脆性破坏。发生板端剥离破坏时，界面剪应力将铝合金板板端从梁体分离，破坏界面平行于板面，从板端向跨中发展。发生中部裂缝剥离破坏时，界面剪应力将梁中部裂缝间的混凝土块体从梁体撕裂，沿纵筋向板端发展。

图9 试验梁破坏方式Fig.9 Failure modes of test beams

试验梁裂缝发展态势基本相同，加载至10%～25%极限荷载Pu时，纯弯段开始出现竖向裂缝，裂缝一出现就上升到一定的高度；加载至0.5Pu左右时，弯剪段出现斜向裂缝，所有裂缝宽度和高度随着裂缝变大而变大。图10给出了SL-4-U1的裂缝分布展开图。图10中，最上面一排数字代表该点与梁的支座之间距离，单位为cm，裂缝处数字代表该裂缝出现时千斤顶施加给梁的荷载值，单位为kN。

图10 SL-4-U1裂缝展开图Fig.10 Unwinding diagram of the cracks on the surfaces of SL-4-U1

图11为SL-4-U1在三分点荷载P=20、40……100 kN作用下截面应变沿梁高度方向分布图。图中纵坐标x代表到梁底的距离，横坐标ε代表相应位置截面应变。可以看出，当荷载增大时，中和轴向梁顶移动，截面平均应变沿截面高度方向呈线性分布，符合平截面假定。说明铝合金板和RC梁连接良好，连接能有效地抵抗二者的相对滑移，共同抵抗外力，有很好的承载性能。

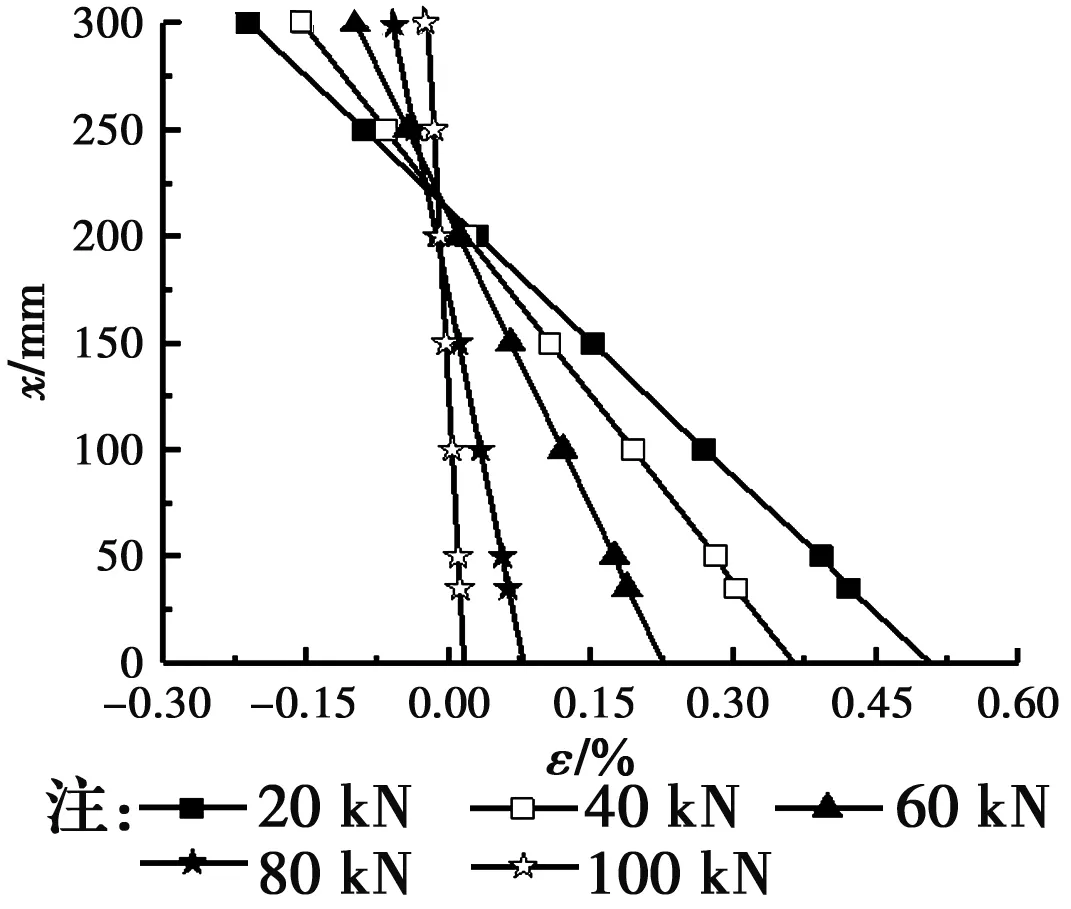
图11 SL-4-U1应变分布Fig.11 Strain distribution of SL-4-U1

图12给出了试验梁三分点荷载P-跨中挠度f曲线。由图12可以看出，适筋破坏的试验梁不但具有很好的承载能力，而且具有很好的延性，剥离破坏的试验梁承载能力和延性均有所降低。

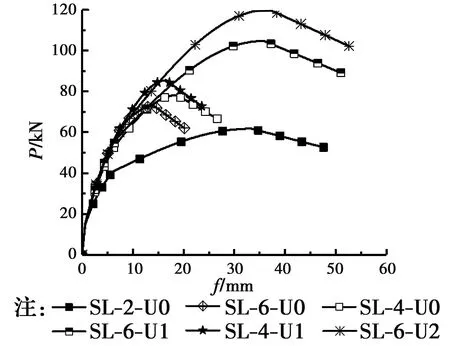
图12 荷载-挠度曲线Fig.12 Load-deflection curves

图13给出了试验梁三分点荷载P-铝合金板应变εa曲线。由图13可以看出，相对于剥离破坏的试验梁，适筋破坏的试验梁利用了铝合金板强度的同时，发挥了铝合金板良好变形的特性，铝合金板最大应变εa介于0.6%～0.8%，试验梁具有很好的延性。

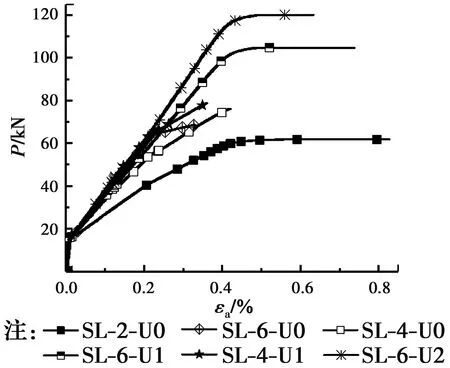
图13 荷载-铝合金板应变曲线Fig.13 Load-strain of AAP curves

2.4 界面剪应力的试验解

设图2铝合金板微元体厚度ta，宽度ba，正应力σa，则其截面积Aa=bata，将轴力Na=σabata代入式(2)，有

(20)

铝合金板正应力σa可以由应变片测得的正应变εa根据式(21)得到。

(21)

这样，由相邻两点的正应力σa, i、σa, i+1可以得到其间的界面剪应力

(22)

式中：Δi,i+1是第i个和第i+1个应变片的间距，试验中Δi,i+1=50 mm。

这样，根据式(21)，由试验测得的铝合金板应变片的读数εa,i，可以得到铝合金板各点应力σa, i，继而由式(22)即可得到各点的界面剪应力试验值τi。表5以试验梁SL-2-U0在三分点荷载P=10 kN作用下为例，给出了界面剪应力试验值τi求解过程，表中x为该点与铝合金板端的距离，考虑结构对称，仅给出了0～1 000 mm内界面剪应力。

表5 界面剪应力试验值求解过程(SL-2-U0，P=10 kN)Table 5 Solving process of test value of interfacial shear stress(SL-2-U0，P=10 kN)

2.5 界面剪应力的影响因素

根据试验梁在三分点荷载P=50 kN作用下粘结界面的剪应力试验值，做出界面剪应力的影响因素柱状图，如图14所示。由图14可知：

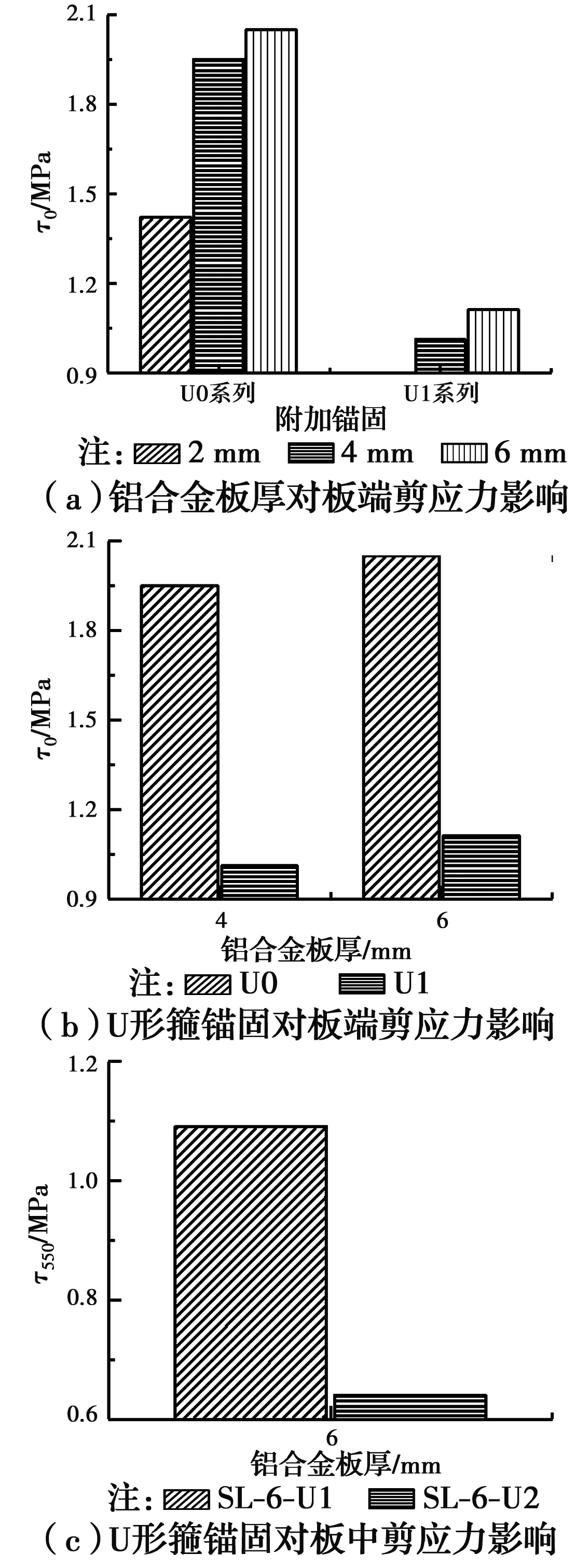
图14 界面剪应力的影响因素Fig.14 Influencing factors on interfacial shear stress

1)铝合金板厚度越大，板端剪应力τ0越高。如图14(a)所示，当不设U形箍锚固时(即图14(a)中的U0系列)，试验梁SL-2-U0、SL-4-U0、SL-6-U0在相同荷载(即P=50 kN)作用下，板端剪应力τ0分别为1.42、1.95和2.05 MPa；当在板端设置U形箍锚固时(即图14(a)中的U1系列)，试验梁SL-4-U1、SL-6-U1板端剪应力τ0从0.99 MPa增加到了1.11 MPa。式(16)表明，界面剪应力与铝合金板厚及其应力变化率之乘积成正比。因而铝合金板厚度变大，界面剪应力随之变大。

2)在板端设置U形箍锚固后，板端界面剪应力τ0变小。如图14(b)所示，铝合金板厚ta=4 mm时，板端增设U形箍的试验梁(SL-4-U1)板端剪应力τ0=0.99 MPa，比SL-4-U0的板端剪应力τ0=1.95 MPa要小；同样，SL-6-U1的板端剪应力τ0=1.11 MPa，小于SL-6-U0的板端剪应力τ0=2.05 MPa。由于铝合金板将部分界面剪应力通过U形箍传递给RC梁，从而铝合金板-结构胶-RC梁界面的剪应力变小。

3)在梁的三分点处设置U形箍后，该处粘贴界面的剪应力τ550变小(U形箍距离板端550 mm，故其剪应力用τ550表示)。如图14(c)所示，SL-6-U2的界面剪应力τ550=0.64 MPa，小于SL-6-U1的界面剪应力τ550=1.09 MPa。其原因和板端设置的U形箍相同。

3 界面剪应力的理论解和试验解对比

为了与界面剪应力的理论解对比，图15给出了无附加锚固的铝合金板加固RC梁SL-2-U0、SL-4-U0和SL-6-U0在三分点荷载P=10、20和40 kN作用下铝合金板粘贴界面剪应力分布曲线的试验结果。

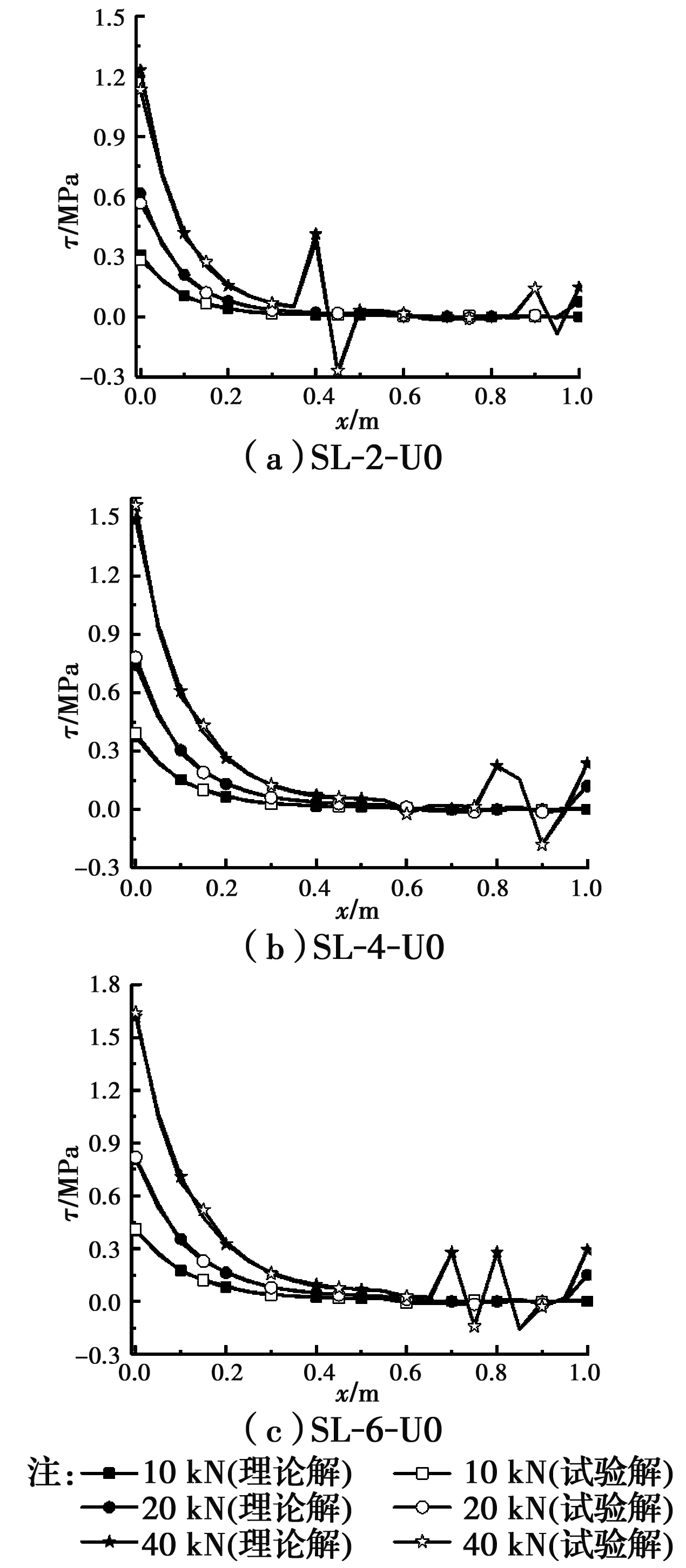
图15 界面剪应力分布试验曲线和理论曲线对比Fig.15 Comparisons of interfacial shear stress distribution curves between the test and the theory

取l=2 700 mm、l0=350 mm、l1=900 mm，结构胶、混凝土和铝合金板等材料力学性能取表1～表3中相应数值，RC梁截面惯性矩Ic及形心轴与底边距离y0按试验梁裂缝开展实际情况确定，由式(7)求得λ和γ的值，将λ和γ的值代入式(14)，得到积分常数C1～C6，继而由式(10)求得界面剪应力τi的理论解。为了便于和试验结果对比，将相应试验梁粘贴界面剪应力理论结果，一并列在图15中。图15中横坐标x为与铝合金板左边板端的距离，由于结构对称，只给出0～1 m的剪应力。

从图15可以看出，SL-2-U0、SL-4-U0和SL-6-U0等3根试验梁的铝合金板粘贴界面剪应力分布曲线的理论解和试验解相差不大，二者符合较好。在10 kN荷载作用下，铝合金板粘贴界面剪应力在板端取得最大值，然后迅速下降，在弯剪区(x≤550 mm)时略大于零，曲线平行横轴，进入纯弯区(x>550 mm)剪应力基本为零。在20、40 kN荷载作用下，受拉侧混凝土出现裂缝，裂缝处混凝土退出工作，拉力由铝合金板和钢筋承担，铝合金板正应力的变化使得裂缝处界面剪应力激增，曲线呈现波动。

界面剪应力在板端取得最大值，表6给出了SL-2-U0、SL-4-U0和SL-6-U0在三分点荷载P=15、37.5和60 kN作用下铝合金板板端界面剪应力的理论值τ01、试验值τ02和二者相对误差δ，δ=(τ01-τ02)/τ02。从表6可以看出，理论值τ01和试验值τ02符合较好，相对误差δ最大值小于5.37%，验证了理论方法的可靠性。

表6 板端剪应力理论值与试验值Table 6 Theoretical and test plate endpoint shear stresses

4 界面剪应力特性分析

4.1 界面剪应力分布曲线

为了分析界面剪应力的变化规律，利用三分点加载的铝合金板加固RC梁界面剪应力的理论解(式(10)、式(14))，材料性能、梁参数及截面惯性矩Ic按试验梁裂缝开展实际情况选取，图16(a)给出了SL-2-U0在0.1Pu、0.3Pu、0.5Pu、0.7Pu和0.9Pu作用下的剪应力分布曲线(Pu为试验梁的极限荷载)。从图16(a)可以看出：

1)在0.1Pu作用下界面剪应力在板端取得最大值，然后迅速下降到零值附近，其后应力基本没有变化。

2)在0.3Pu作用下试验梁纯弯区梁底混凝土出现裂缝，裂缝所在截面应力发生重分配，铝合金板应力发生突变，纯弯区界面剪应力曲线呈波浪状。

3)随着荷载的增大，混凝土裂缝变多，界面剪应力除板端应力变大以外，其波浪也越来越多；当荷载不大于0.5Pu时，波浪只在纯弯区出现；荷载达到0.7Pu后，弯剪区裂缝的出现使得该区域剪应力也呈波浪状。

为了与三分点加载的铝合金板加固RC梁界面剪应力分布曲线进行比较，材料性能、梁参数及截面惯性矩Ic相关参数按试验梁SL-2-U0选取，并按荷载相等的原则将三分点集中荷载P等效为跨中集中荷载P1和均布荷载q，SL-2-U0的极限荷载Pu为61.77 kN，则三分点集中荷载P=0.1Pu、0.3Pu、0.5Pu、0.7Pu和0.9Pu时，跨中集中荷载P1=2P，其值分别为12.35、37.06、61.77、86.48、111.19 kN；均布荷载q=2P/l，其值分别为4.58、13.73、22.88、32.03、41.18 kN/m。分别根据跨中集中荷载P1作用下的界面剪应力的理论解式(16)、均布荷载q作用下的界面剪应力的理论解式(18)，得到界面剪应力分布曲线，如图16(b)和16(c)所示。从图16中可以看出，3种荷载作用形式的界面剪应力分布曲线具有相似的分布规律：在板端取得最大值，然后以曲线形式迅速衰减到横轴附近。另外，由于无法预知RC梁裂缝分布情况，跨中集中荷载和均布荷载作用下的界面剪应力计算时全梁采用统一的梁参数及截面惯性矩，曲线是一条光滑曲线，与实际界面剪应力分布曲线略有差异。事实上，由于RC梁裂缝开展的随机性，无法采用一给定的理论解预测带有随机性的界面剪应力的具体分布。由于界面剪应力的最大值在板端取得，该值理论值与试验值符合良好，与裂缝无关，界面剪应力最大值是工程上最主要的关注点，并且理论解能够反映界面剪应力的变化规律，因此不影响理论解对实际工程的指导价值。

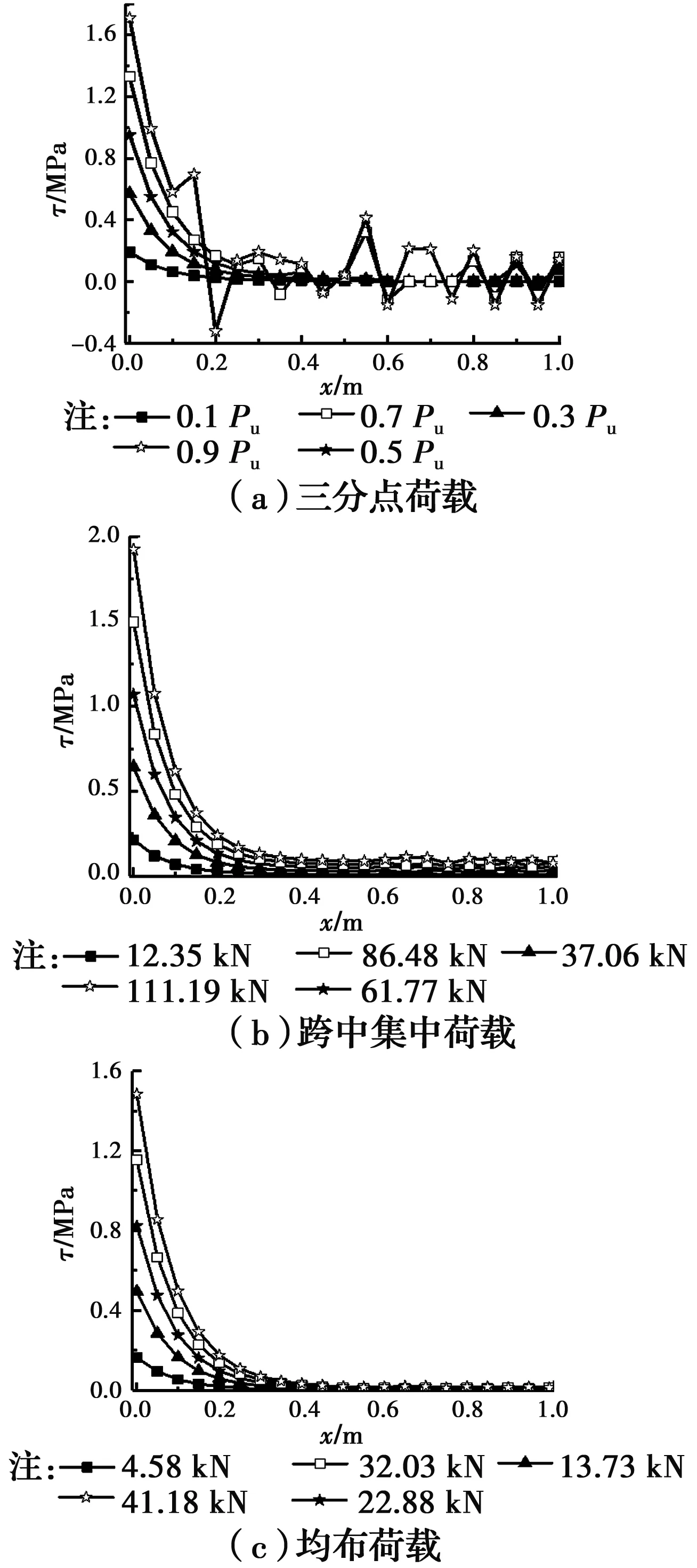
图16 界面剪应力分布曲线Fig.16 The curves of interfacial shear stress distribution

4.2 板端界面剪应力

最大界面剪应力是工程中最主要的关注点，最大界面剪应力在板端取得。之前根据试验结果讨论了铝合金板厚和附加锚固对最大界面剪应力τmax的影响，现在利用常见荷载作用下的界面剪应力最大值理论解式(15)、式(17)和式(19)、讨论荷载形式、板端与支座距离l0和结构胶厚度tp对最大界面剪应力τmax的影响。表7给出了三分点集中荷载P=25 kN、跨中集中荷载P1=2P=50 kN和均布荷载q=2P/l=18.52 kN/m的铝合金板加固梁的板端界面剪应力，除表中给定的参数外，其他参数均按试验梁SL-4-U0选取。比如，当表中给定板端与支座距离l0时，其结构胶厚度tp按试验中3 mm选取；当表中给定结构胶厚度tp时，其板端与支座距离l0按试验中350 mm选取。

表7 最大界面剪应力理论值Table 7 The maximum interfacial shear stresses N/mm2

从表7可以看出，相同条件下不同荷载形式的最大界面剪应力，跨中集中荷载时最大，均布荷载时最小，亦即荷载分布越分散和越均匀，最大界面剪应力τmax越小；当其他参数相同时，板端与支座距离l0越小，最大界面剪应力越小，加固时宜取较小的l0值，当然l0越小，所需的加固材料越多；当其他参数相同时，结构胶厚度tp越大，最大界面剪应力越小；但实际工程中并不是结构胶厚度tp越大越好，结构胶厚度tp越大，发生胶层撕裂破坏的可能性变大，对施工技术和结构胶质量提出了更高的要求。