直观引发归纳 转化明晰算理——以人教版《义务教育教科书·数学》五年级上册“小数乘小数”为例

陈为强

（江苏省徐州市贾汪区实验小学）

谈起推理，很多人不由自主地想起中学几何证明中的演绎推理，其实推理并不是中学几何的“专利”，它在数学的其他领域也被广泛运用。然而，计算教学中的推理运用往往被师生所忽略和遗忘，本文仅以人教版《义务教育教科书·数学》五年级上册“小数乘小数”为例，谈谈归纳推理和演绎推理在计算教学中的有效运用。

一、借助几何直观，进行归纳推理

借助几何直观能把抽象的结论变得形象化、可视化。六年级的“分数乘以分数”几何模型的呈现方式可使学生很形象地理解“分数乘分数”计算的算理和算法。利用小数和分数的密切关系，借鉴这种几何直观图，可使学生对小数乘以小数的计算结果从直观感知走向直观理解，进而引发直观猜测、直观推理。

如可以出示探索题：王老师家装修房子，购买了一种长0.6米，宽0.4米的长方形瓷砖，每块瓷砖的面积是多少平方米？

师：怎样列式计算？

生：0.6×0.4= 。

师：这道题与以前的小数乘法有什么区别？

生：以前学的是小数乘整数，这题两个数都是小数。

师：这就是今天要学习的内容“小数乘小数”（板书课题），你会算吗？（学生尝试）

生：0.6×0.4=2.4，因为 0.6 和 0.4 都是一位小数，所以乘积也是一位小数为2.4。

生：0.6×0.4=0.24，因为 0.6 米=6 分米，0.4 米=4分米，6×4=24（平方分米），24（平方分米）=0.24（平方米）。所以0.6×0.4=0.24。

师：哪位同学明白他的方法？

生：他是把小数乘法借助单位换算转化为整数乘法，算完后又把单位换算回来的。

师：这位同学很善于发现别人的闪光点，还有别的方法吗？下面的图你能看懂吗？

生：这是一个边长为1 米的正方形，阴影部分是长6 分米，宽4 分米的小长方形，其面积占大正方形的24/100，用小数表示为0.24，所以0.6×0.4=0.24。

师：能从图中看到乘积，不简单，如果让你计算0.6×0.9 ，你会吗？

生：可以假设 0.6 和 0.9 的单位为米，转化为分米进行计算，结果为54 平方分米，然后换算以平方米为单位，算出0.6×0.9=0.54。

生：我是借助画图的方式，从下图中可以看出0.9×0.6 占大正方形的面积的 54/100，所以 0.9×0.6=0.54。

师：这两题在方法上什么相同之处？

生：都是借助单位换算转化成整数乘法，算完后，再通过单位换算求出原来的结果，还可以借助画图的方法表示两个小数相乘的结果。

生：我还发现两个一位小数相乘，积就是两位小数。

师：仅仅从两个例子就得到这个结论，是否正确，还有待验证。

学生独立探索小数乘小数的计算方法，有的学生借助已有的小数加减法的计算经验进行类比推理，造成乘积中小数点的位置错误；有的学生借助生活经验，利用单位换算转化成整数乘法进行计算，然后进行单位还原求出结果；还有的学生利用小数和分数的关系，数形结合，借助直观模型形象地诠释0.6×0.4的结果。接着，教师出示0.6×0.9，学生运用刚刚学到的方法，利用转化表征或者图形表征来呈现结果。经此探究，引发了学生的直观洞察，他们进行不完全归纳推理：两个一位小数相乘，积是两位小数。因为不完全归纳推理的结论具有或然性，所以教师要引导学生对发现进行验证。

二、借助演绎推理，明确背后算理

因为不完全归纳法推导出来的结论具有或然性，可能是正确的，也可能是错误的，因而对结论的验证必须要经过演绎推理，只有通过演绎推理严格论证才能确定结论的必然性。而最新研究表明，10～11岁是儿童演绎推理认识的快速发展期，因此，作为数学教师，我们可以依据自己的教学内容，逐步渗透之，只要学生能“够得着”，我们就要开展演绎推理，让学生走出依靠直观形象和感性经验进行合情推理的框框，展开有根有据、有条有理的论证，让学生明白其中蕴含的道理，帮助学生树立理性思维。下面是王老师家房间和外面阳台的平面图。

师：你能提出什么问题？请列出算式。

生：房间的面积多少平方米？列式为3.8×3.2。

师：大家尝试一下？

生：利用单位换算把 3.8 米和 3.2 米转化为 38 分米和32 分米，38 与32 积为1216，1216（平方分米）=12.16（平方米），所以3.8×3.2=12.16。

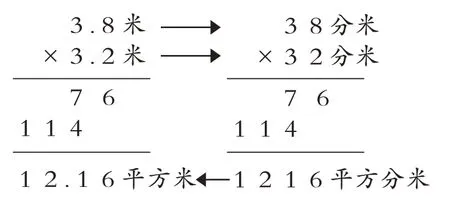
师：不借助单位换算的方法，能否说明小数乘法的计算道理？

生（皱着眉头）：从 3.8 变成 38 扩了 10 倍，3.2 变成32也扩大10倍，积也会扩大的，那怎么办？

生（激动地说）：我明白了，3.8 和3.2 分别扩大10倍是 38 和 32，积就扩大 100 倍，然后把 38 和 32 的积缩小100 倍是12.16。（结合学生的说明完成板书如下）

生：小数乘法是转化成整数乘法计算的，然后点上小数点。

师：一道题带给大家的感悟不少，会算阳台的面积吗？

（学生独立计算后展示）

生：我是按照小数点对齐计算的，算完后把小数点拉下来积是43.7，大家同意吗？

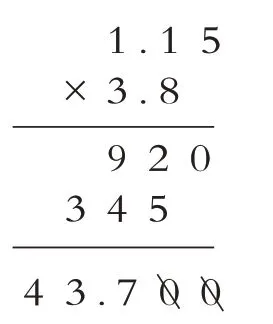
生：我不同意，如果把两个小数都看大一点，分别是2和4，乘积才是8，这题中积比8小。

师：利用估算初步判断1.15×3.8不等于43.7，正确的该如何计算呢？

生：按照末尾对齐来计算，把 1.15 和 3.8 分别扩大 100 倍和 10 倍为 115 和 38，乘积就扩大 1000 倍，115与38的积是4370，最后把积缩小1000倍为4.37。

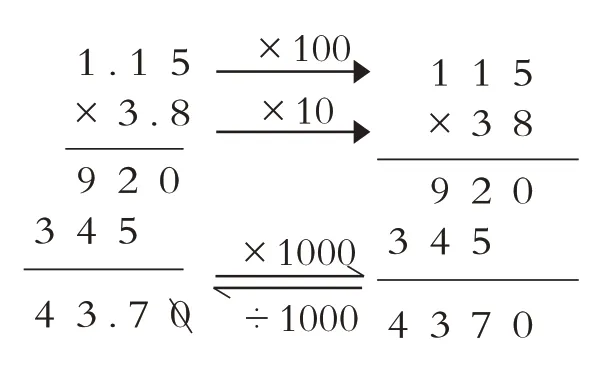
师：算出的积符合刚才估算的结果吗？（学生赞同）这位同学不仅说出了结果，还说明了原因。它们计算时有什么相同点？

生：都是转化成整数乘法进行计算的。

生：小数乘法列竖式计算最好末尾对齐。

师：为什么小数乘法列竖式计算末尾要对齐？

生：小数乘法列竖式计算如果小数点对齐，积的小数点和乘数的小数点不一定对齐。它和小数加减法不一样，小数加减法计算时小数点对齐，结果的小数点和上面小数点也对齐。

师：这几位同学讲得很好，能从小数乘法计算本质说明末尾对齐的合理性。

计算的本质就是推理，就是寓理于算的过程，本环节学生在刚刚获得两个一位小数相乘的算法后，能够利用单位换算完成3.8×3.2 的计算。但是学生对小数乘法的理解仅停留在“知其然”的表面上，没有理解藏在背后的算理。教师的适时追问“不借助单位换算转化的办法能否说明小数乘法的计算道理”“ 逼迫”学生进行了深入思考，通过箭头的指向打通了小数乘法和整数乘法之间的联系。学生有条有理地阐释了其中乘数和乘积的变化，逐步理解了小数乘法是利用积的变化规律转化成整数乘法计算，然后把积缩小相应的倍数求出原来结果的算理。转化过程的每一步都是严谨而有根据的，诠释了演绎推理的魅力，使学生明晰了背后的算理，从而“知其所以然”。教师并没有满足于学生对3.8×3.2 算理的理解，而是请其独立计算1.15×3.8。学生展示各自的算法并有理有据地阐释，通过对比，学生真正明白小数乘法末尾对齐的根本所在——都是转化成整数乘法进行计算，有效消除了小数加减法给小数乘法计算带来的负迁移，使其由对小数乘法由关注外在形式走向深刻理解内在结构。

三、注重说理训练，总结计算方法

通过不完全归纳法学生发现了小数乘法计算的关键点——乘积小数的位数和两个乘数小数位数之间的关系，然后通过演绎推理证明了开始的猜想。经历两种推理，学生进一步明确了小数乘法计算算理。算理是内隐的，算法是算理的外在表达方式，于是算法的总结完善就成为计算教学的必然。

师：你能给下面各题的积点上小数点吗？

生：0.87×0.9 两个乘数分别扩大 100 倍和 10 倍，转化成87×9=783，然后积再缩小1000 倍，成为0.87乘0.9，结果是0.783。

师：积的小数位数是怎样确定的？

生：8.7和0.9都是一位小数，积7.83是两位小数,72.9 和 0.04 分别是一位和两位小数，乘积 2.916 是三位小数。

生：我发现“积的小数位数就是两个乘数中小数位数的和”。

其实，泰勒的“第一等工人是指那些雄心壮志、从事适合自己工作的人”。用现在的话说就是用人坚持“人岗匹配”，持有这种观点的泰勒没有错。他认为人的差别不在智力高低，而在于渴望成功的愿望。所以，泰勒描述的“第一等工人”不是超人，而是我们大多数的普通人。

师：大家同意这位同学的发现吗？

生：我不同意，第三题 16.5×0.6=9.9，两个乘数都是一位小数，积还是一位小数。

生：不对，积 9.9 是原来乘积 9.90 这个两位小数化简得来的。

生：最好在刚才发现加上几个字变成“积的小数位数在没有化简之前等于两个乘数中小数位数的和”。

师：加上几个字就不容易产生歧义了，为什么存在这一现象呢？

生：如果两个乘数分别是两位和三位小数，转化成整数时分别扩大100 倍和1000 倍，乘积就扩大100000倍，积缩小100000倍就是五位小数。

师：如果不举事例，能不能说明这一结论？

生：小数乘法是转化成整数乘法来计算的，两个乘数分别有a位和b位小数，转化成整数分别要向右移动a位和b位，所得乘积向右移动（a+b）位。要求小数的乘积，就要把积向左移动（a+b）位，所以乘积的小数位数在没有化简之前等于两个乘数中小数位数的和。

师：这位同学用字母说明乘数小数位数与乘积中小数位数之间的关系，这样就能把所有情况全部概括了。谁能总结小数乘法的计算方法？

生：小数乘法是按照整数乘法的计算法则进行计算的，最后数出两个乘数一共有几位小数，就从积的右边起数出几位点上小数点。

学生把对算理的理解用自己的语言表征了出来，通过几道题的训练，学生发现小数乘积中小数位数和乘数小数位数的和之间有着直接的关系，借助两个小数转化成整数扩大的倍数以及积的变化规律对此关系作以深刻诠释，使得“算理”和“算法”相融而贯通。

四、沟通知识联系，拓展学生思维

有效的练习既注重“练（训练）”，更注重“习（习得）”，从“习”对“练”的过程的反省和思考，促使“练”与“习”向纵深处发展。作为练习，既要聚焦小数乘法的难点——乘积中小数位数的确定，又要注重发展学生思维，提升数学核心素养。

师：看下面的算式，根据小数乘积的小数位数给乘数点上小数点。

生：第一题应该为7.29×0.4=2.916，因为积为三位小数，乘数0.4 为一位小数，所以另一个乘数应为两位小数7.29。

生：第二题积在没有化简前为两位小数，所以两个乘数小数位数一共是两位，可以写成1.65×6=9.90；16.5×0.6=9.90；165×0.06=9.90三种情况。

师：这两题有什么区别？

生：第一题的答案只有一种，因为乘积与其中一个乘数的小数位数确定，另一个乘数的小数位数就确定了。

生：第二题要注意乘积没有化简之前是两位小数，所以在给两个乘数点小数点时，只要两个乘数一共有两位小数就可以了，所以本题答案不止一个，存在多种可能。

数学练习不求全，但求变，该练习引导学生根据小数乘法的计算法进行逆向推理，在“积”的不变中寻求两个乘数的状况，在“变与不变”中让学生不仅达到对小数乘法计算的通透理解，而且还发散学生的思维，增强思维的开放性。