基于响应面法的多材料优化模型与应用

柴 灏，黄 仪，张 征，卢纯福，鲁聪达

(浙江工业大学 机械工程学院，浙江 杭州 310014)

0 引言

传统的优化设计在汽车行业轻量化中很难同时兼顾各方面的性能，往往只能得到局部最优解，而汽车行业的轻量化设计必须综合考虑多个学科对其整体性能的影响，实际上是一个多目标优化设计问题[1]。结构优化是实现轻量化目标的重要手段之一，许多学者提出在汽车结构中应用轻量化材料(碳纤维、塑料、镁合金、高强度钢[2])以达到轻量化目的。Fang等[3]利用多项式响应面法建立了质量、刚度、模态的近似模型，并将其运用到汽车车门的多目标优化中;夏玉峰等[4]利用响应面法构建了装配间隙的近似模型，并将其运用到汽车B柱装配质量的优化中;白俊峰等[5]利用二阶响应面模型，建立了剪切位移、弯曲角度、加速度峰值的近似模型，并将其运用到汽车保险杠的多目标优化中;张勇等[6]利用多项式响应面法构建了B柱加速度、一阶扭转模态、质量的近似模型，并运用到整车的轻量化设计中。已有文献调研表明，大多数研究工作仅局限于结构优化(材料为单一材料)，尚未见考虑多种材料替换与优化而形成的多材料、多目标优化模型及应用的研究。

本文提出一种基于响应面法的多材料、多目标模型并应用其对汽车座椅进行轻量化设计。将汽车座椅骨架各零部件的材料类型作为离散变量，厚度作为连续变量，以总质量最小化和一阶模态最大化作为优化目标，利用响应面法构建近似模型进行寻优，最后对优化解进行强度校验。该模型在对结构进行优化的同时，能充分利用不同材料的优势，控制使用新材料所带来的成本增长。

1 多目标优化模型

考虑到在多目标优化问题中直接调用有限元软件进行仿真模拟会带来庞大的计算量，计算成本较大，因此本文利用最优拉丁方实验设计方法在样本空间采样，构建基于响应面法的多项式近似模型，然后在优化问题中调用该近似模型，以缩短计算时间、提高优化效率。

1.1 响应面法

响应面法是一种运用简单的表达式(通常是低阶的多项式)，拟合实际的设计变量与响应之间的关系，从而构建经验模型的拟合方法[7]。多数情况下，需要拟合的设计变量与响应的关系都是未知的，因此需要以试验设计和数值分析为基础，在自变量的区域内进行采样，在样本空间内寻求合适的逼近式来近似拟合自变量与实际函数的关系。该方法能利用较少的采样次数，在设计空间内得到比较精确的近似关系，并用简单的多项式表达出来，大大缩短了构建近似模型所需要的计算时间[8]。本文如下采用二阶响应面模型：

(1)

近似模型建立以后需要对其拟合精度进行评估。假设采样点总偏差平方和为Qz，残差平方和为Qc，回归偏差的平方和为Qh，表达式如下：

Qz=Qc+Qh。

(2)

(3)

1.2 优化拉丁方试验方法设计

优化拉丁方抽样方法通过分层抽样获得样本点数据，侧重于控制采样点的位置，避免在小区域内发生重叠。其基本原理是将A个随机变量划分为B个等概率的区间，从而将整个采样空间划分为BA个等概率区域，因此B个采样点必定会落入到BA中的某一个区域，且样本点将等概率地分散到整个采样区间。2因素9水平的优化拉丁方采样设计如图1所示。本文利用优化拉丁方抽样方法抽取180个样本点。

1.3 多目标优化模型与流程

对多个子目标同时实施最优化的问题称为多目标优化问题，实际的工程优化问题大多数属于多目标优化问题。各目标之间一般是互相冲突的，某子目标的改善可能引起其他子目标的降低，即同时使多个子目标均达到最优是不可能的，因此设计人员需要进行多目标的比较，并进行权衡和折中。常见的多目标优化问题的数学表达式为

minF(X)=[f1(X),f2(X),…,fi(X)]。

s.t.

gj(X)≤t;

i=1,2,…,m，j=1,2,…,n，k=1,2,…,p。

(4)

在多材料、多目标的优化问题中，可按如下步骤求解：

步骤1根据具体的优化问题，确定优化目标、材料变量以及设计空间范围等。

步骤2利用最优拉丁方试验方法在样本空间内生成构建近似模型所需样本点，对每个样本点递交有限元软件进行仿真计算，得出对应样本点的响应值，以获得的样本点数据。建立设计变量与响应函数的二阶响应面近似模型并校核模型精度是否满足要求，若精度较低，需要在试验设计中增加样本点个数，重构响应面模型，直到模型精度符合要求。

步骤3将构建的响应面模型应用到优化求解过程中，选择带精英策略的快速非支配排序遗传算法(fast elitist Non-dominated Sorting Genetic Algorithm, NSGA-Ⅱ)[10]对优化问题数学模型进行求解，最终得到该优化问题的Pareto前沿解集。具体的优化流程如图2所示。

2 基于响应面法的汽车座椅多目标优化

汽车座椅作为汽车内外饰的重要组成部分，其动态特性会严重影响驾驶员的安全性和舒适性[11]，因此在进行轻量化的同时，考虑对一阶模态进行优化具有重要意义。在构建座椅骨架总质量和一阶模态的响应面模型时，需要采用有限元方法对样本点的模态进行求解，因此首先需要在Hypermesh中建立座椅骨架的有限元模型，然后定义优化问题进行采样，在Radioss求解器中对样本点进行仿真，根据得到的样本点响应构建近似模型，最终运用NSGA-Ⅱ优化算法进行寻优，确定最终优化方案。

2.1 有限元模型的建立及设计变量选取

为了便于在Hypermesh中进行有限元建模，经过前处理，简化了一系列小的几何特征，最终得到座椅骨架的有限元模型,如图3所示。不带头枕的座椅骨架主要由薄壁结构构成(各零部件的厚度被认为是均匀的)，有限元模型中使用了壳单元、实体单元和梁单元，梁和rbe 2单元用于模拟螺栓和铆钉连接方式，rigid单元用于模拟焊缝连接方式。有限元建模时需严格控制三角形单元的数量、翘曲、最大和最小内角等条件，该模型共有163 933个单元和174 311个节点组成。

在Hypermesh模块中建立好整椅的有限元模型后，递交Radioss求解器对座椅模型进行模态分析。在有限元分析中，4个底脚螺栓周围的所有节点均受到全约束，原始模型的一阶模态如图4所示，按国标GB11550-2009《汽车座椅头枕强度要求和试验方法》对座椅骨架进行头枕静强度仿真，其头枕最大位移量如图5所示。

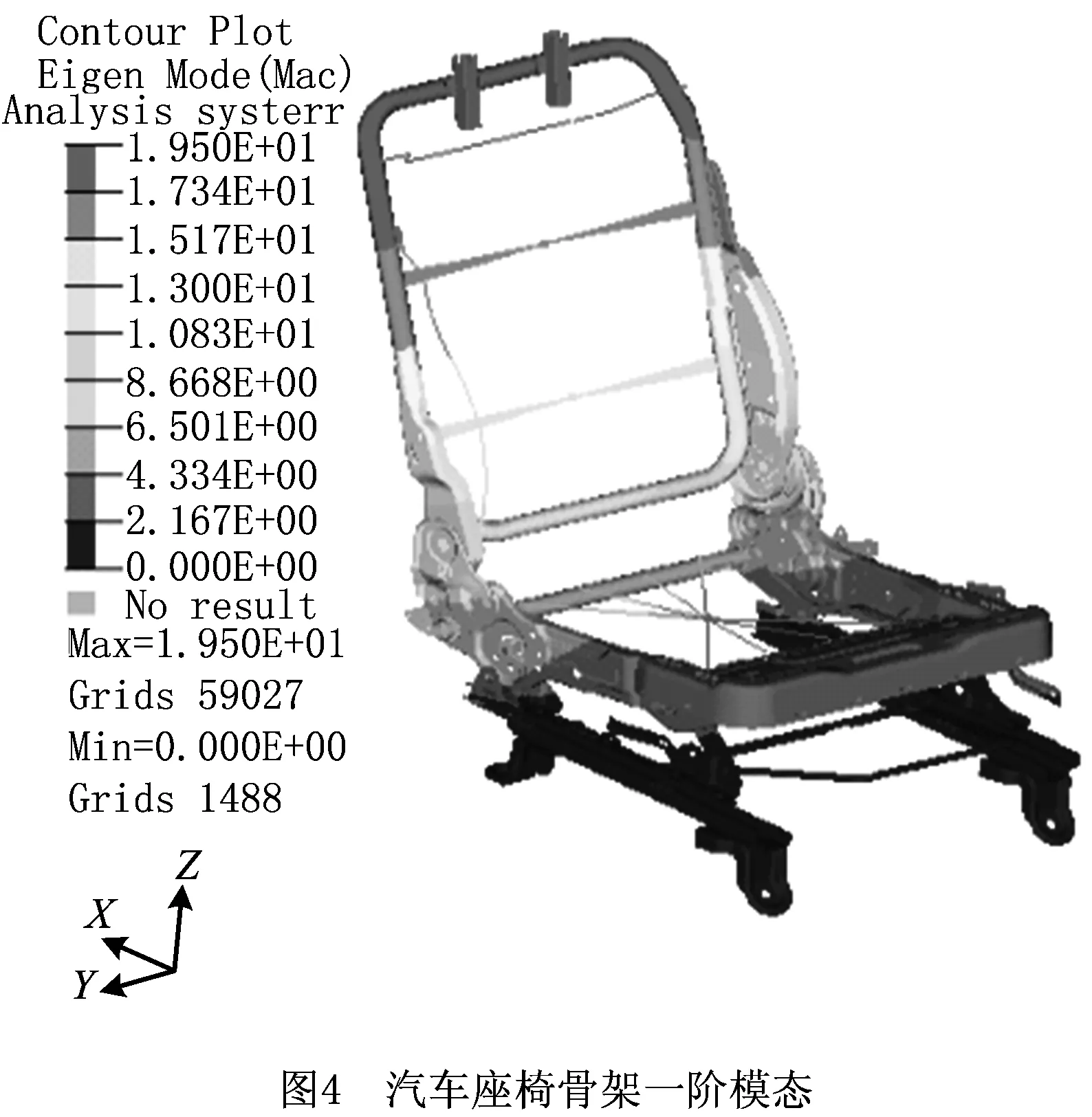
在满足其他性能的前提下，提升一阶模态的同时实现轻量化设计，所选择的部件必须在整椅中具有一定质量比，但避免选择结构的核心部件。最终选出7个零部件：头枕导套支撑管、靠背弯管、内外侧背连接板、内侧座连接板、外侧座连接板、座盆、前支撑管。

2.2 定义优化问题

选择图3中7个零部件的材料属性和厚度作为设计变量，由于零部件4和零部件5的材料类型需要相同，它们的材料类型被视为一个设计变量，因此本优化问题共定义了13个设计变量。每种材料都包含其自己的材料属性如弹性模量、泊松比、密度等，如果单独将各个属性单独作为变量会使得问题复杂化，因此本文将材料类型而不是单一的材料属性作为设计变量[12]，如表1所示，每个备选材料都被分配了相应的材料编号，记为mi。

表1 各材料编号

该优化问题定义为：

minM=M(Ti,mi);

maxf=f(Ti,mi)。

s.t.

i=(1,2,…,7);

mj∈(1,2,3);

j=(1,2,…,6)。

(5)

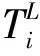
表2 零部件厚度上下限 mm

2.3 响应面模型的构建

本优化问题定义了13个设计变量和两个目标函数，为了构建二阶响应面模型，首先采用优化拉丁方试验方法在样本空间生成180个样本点，通过有限元仿真计算，得到样本点对应的响应值。将样本数据导入Isight软件构建二阶响应面模型，并评估其精确度。表3所示为响应面模型的误差，表中M和f分别表示座椅骨架总质量和一阶模态频率，它表明该响应面模型精度足够，可以用于后续的多目标优化求解。

表3 响应面模型精度评估

2.4 多目标优化结果分析

在Isight软件中基于2.3节建立的响应面模型，用NSGA-Ⅱ优化算法进行求解，对应的优化算法参数设置如表4所示。

表4 NSGA-Ⅱ的优化参数设置

经过NSGA-Ⅱ算法寻优后，最终获得Pareto前沿解集，如图6所示。

最终选出3组优化解，详细设计变量及其响应如表5所示。

表5 汽车座椅骨架的Pareto优化解

由于这3组方案一阶模态只有轻微差异，优化方案3在本研究中被视为最优方案。将第三组方案结果与原始模型比较(如表6)可以发现，在一阶模态提升10%的同时，头枕位移量减小23%，说明优化后的结构系统刚度变大，座椅骨架的总质量减少了21%。

表6 优化方案与初始方案对比

3 优化方案强度校核

将初始有限元模型按照上述优化方案的模型参数进行设置，并依据国标GB15083-2006《汽车座椅系统强度要求及试验方法》、GB11550-2009《汽车座椅头枕强度要求和试验方法》对优化后的座椅骨架分别进行靠背强度校核以及头枕静强度校核。

依据国标GB15083-2006《汽车座椅系统强度要求及试验方法》，对座椅R点对座椅骨架施加530 N·m的翻转力矩，总体应力云图、危险零部件应力云图如图7所示。危险零件为外侧座连接板，优化方案中该零件使用轻量化材料为高强度钢DP590，屈服极限为340 MPa，抗拉极限为590 MPa。由结果可知，该零部件在加载过程中进入塑性变形阶段，但仍未超出材料的抗拉极限，未造成材料失效，满足该项国标要求。

依据国标GB11550-2009《汽车座椅头枕强度要求和试验方法》，对靠背施加相对H点373 N·m的载荷时，头枕位移量应小于102 mm，且当加载力增加至890 N时，座椅零部件不允许失效。本处校核时，在靠背弯管顶部施加890 N载荷时，头枕位移量、整体应力云图、危险部件应力云图如图8所示。危险零件为外侧座连接板，优化方案使用高强钢DP590，屈服极限为340 MPa，抗拉极限为590 MPa。

由结果可知，该零部件虽进入塑性变形阶段，但未超过材料的抗拉极限，优化方案的座椅骨架能承受住国标规定的890 N载荷，而骨架无破损或脱落，满足该项国标要求。

4 结束语

本文建立了基于响应面法的多材料、多目标优化模型，将混合轻量化材料应用于汽车座椅骨架的轻量化设计中。利用NSGA-Ⅱ算法得到Pareto优化解，并依据相应的国标对优化方案进行强度校核。结果表明：采用多材料、多目标优化模型设计汽车座椅时，在保证座椅强度、刚度等基本要求的同时，可以获得更轻质的汽车座椅，对于汽车座椅的轻量化设计有较好的指导作用。本文所提优化模型基于响应面法建立，下一步将探究其他近似模型是否适用于于本文的优化问题建模。此外，可以考虑汽车座椅的动态性能，对其进行随机激励响应分析、瞬态响应分析、随机振动分析、NVH(noise, vibration, harshness)分析等。