一道高中数学毕业会考题的多种解法与教学建议

夏顺友，王常春，陈治友，汪少祖，刘益波

(1.贵州师范学院数学与大数据学院，贵州 贵阳 550018；2. 遵义师范学院数学学院，贵州 遵义 563006；3.贵阳学院数学与信息科学学院，贵州 贵阳 550005)

0 引言

解析几何是用代数方法解决几何问题的数学理论，是培养六大数学核心素养(数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析)的重要内容之一。高中数学的解析几何内容主要以五种曲线(直线、圆、椭圆、双曲线和抛物线)的定义(满足某种性质的动点集合)、代数形式(各种形式的方程表示)、性质(利用方程中系数特征进行分析)以及各种曲线之间关系(利用方程系数或方程组解情况研究)作为核心研究内容。但是由于该部分内容关键是从几何到代数的方程(组)建立和由方程来确定几何性质、几何关系等，需要较强的数形结合思维，因此是高中数学学习难题之一。

高中解析几何所包含的基本知识涵盖五种曲线的定义表述、方程表述、性质特征，以及直线、圆与圆锥曲线综合问题。另外还涉及五种曲线的极坐标和参数方程。在综合考核中该部分内容常与平面几何、函数、三角函数等知识内容、思想方法结合考查，增加了难度。

下面先简述解析几何的核心知识，然后给出2019年12月贵州省高中数学毕业会考数学第43题(解析几何综合题)的多种解法，接下来提出关于解析几何教学的几点建议。

1 解析几何的核心知识概要

1.1 直线的核心知识

直线的核心知识包括：直线的倾斜角、斜率概念、范围，斜率计算公式，以及两者对应关系，要注意的特殊情形；直线的点斜式方程、一般式方程、斜截式方程、两点式方程和截距式方程以及参数方程、极坐标方程；两直线平行、垂直的关系判定及其逆问题；点到直线距离、相交直线夹角和平行线间距离计算公式；直线族问题等。

注：确定直线一般需要两个独立条件。如已知其过已知点加上斜率两个条件等；特殊直线：垂直于坐标轴、过原点的特征。

1.2 圆的核心知识

圆的核心知识包括：圆的定义、圆的标准方程与一般方程。确定圆的关键是圆心与半径;直线与圆、圆与圆的关系以及德尔塔方法，圆心与直线距离及圆心与圆心之间的距离同半径关系判定方法;另外是圆的参数方程和极坐标方程。

注：解题中要特别注意圆的一些几何特征，如垂径定理等等。还要注意恰当方程的选取。

1.3 圆锥曲线的核心知识

圆锥曲线的核心知识包括：圆锥曲线的第一、二定义，标准方程、一般方程、极坐标方程和参数方程，顶点、焦点，准线、渐近线，长短轴、实虚轴，切线、割线，切线长、弦长，中点弦、焦点弦等问题。

注：确定方程需要两个独立条件(抛物线仅一个)。切线问题对圆、椭圆与双曲线、抛物线差别(封闭曲线的切线的特殊性)。割线与弦长、中点弦和焦点弦特征和一般计算方法及公式。

2 学生答题基本情况和该题的分析及多种解法

2019年贵州省高中数学毕业会考第43题是关于解析几何中直线与圆的方程及直线与圆的关系，并综合不等式、平面几何、参数方程、三角函数和函数最值的题目。其题目如下：

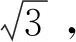
本题满分为10分，(1)与(2)分别为5分和5分。总试卷5万多份，根据评卷系统的最后统计结果，本题平均得分在包含零分卷时是2.08，如果不包含零分卷时，则平均得分是4.31。具体说来，得分为8分至10分的考生比例是1.5%，而得分为4分至7分的考生比例是26.29%，得分为0.5分至3分的考生比例是16.69%，得分为0分的考生比例是51.79%。这说明考生总体上对基础知识、基本技能和基本方法掌握得不好，能拿到本题的优良分数的考生不到2%。接近半数考生虽然能答对问题的(1)部分，但是在准确表达上还不够严谨，并且基本没有利用直线与圆的平面几何特征简洁求解的。特别是问题(2)，绝大部分考生不能求解。还有半数以上的考生对直线与圆的方程等基本知识没有掌握。

该题在考核直线与圆的概念、方程及关系的核心知识和方法之外，综合考核了有约束条件下的函数的最值问题的建模和求解，考核了学生的综合分析和解决问题能力，是此次考试中难度最大的题目。

下面先给出该题问题(1)的多种解法。其中解法一是命题者给出的参考解答。

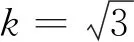
圆心O到直线l的距离为:

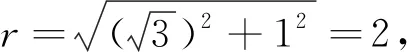
注：命题者意图是直线方程的点斜式，一般式，圆方程的标准式. 直线与圆相切的判定方法.

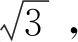
因此，圆O的方程为x2+y2=4.

注：该法借助几何性质，比较直接简单。

解法三：设直线l与圆O交点为C,D(左下右上)，C(x1,y1),D(x2,y2)，则

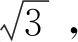
再设圆O的方程为x2+y2=r2，联立直线方程得：

x2+3(x+2)2=r2，即4x2+12x+12-r2=0.

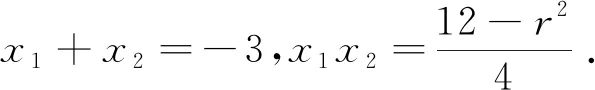
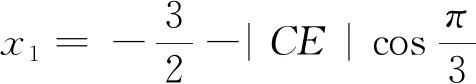
注：该法利用直线与二次曲线截得弦长的一般计算方法并结合几何特征。

解法四：设直线l与圆O交点为C,D(左下右上)，C(x1,y1),D(x2,y2)，则

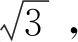
再设圆O的方程为x2+y2=r2，联立直线方程得：

x2+3(x+2)2=r2，即4x2+12x+12-r2=0.

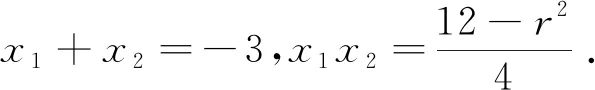
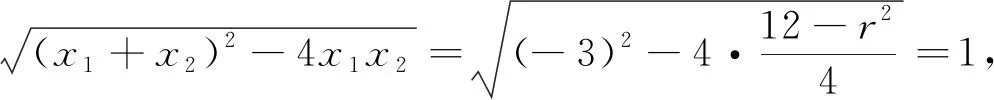
注：该法利用直线与二次曲线截得弦长的一般计算方法并结合待定系数法。

下面再给出该题问题(2)的多种解法。其中解法一是命题者给出的参考解答。

解法一：因为点P(x,y)(x≥0)在圆O上，所以

x2+y2=4.

又A(-2,0),B(4,0)，则

|PA|2=(x+2)2+y2=4x+8，

|PB|2=(x-4)2+y2=20-8x.

所以有

令u=8x+16,v=20-8x，则u+v=36.

因为0≤x≤2，所以16≤u≤32,4≤v≤20.

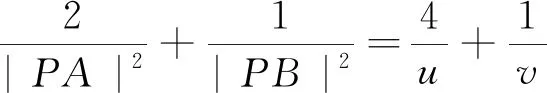
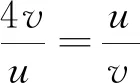
u=24,v=12

注：命题者意图是考核化归思想方法和均值不等式求解最值问题。

解法二：因为点P(x,y)(x≥0)在圆O上，所以

x2+y2=4.

又A(-2,0),B(4,0)，则有

|PA|2=(x+2)2+y2=4x+8，

|PB|2=(x-4)2+y2=20-8x.

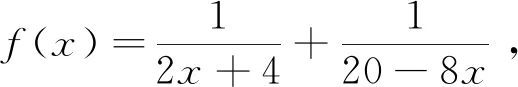
于是由f′(x)=0得，x=1,x=7.

因为点P(x,y)(x≥0)在圆O上，所以0≤x≤2.

因此x=1是所求最小值点。

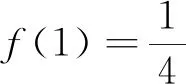
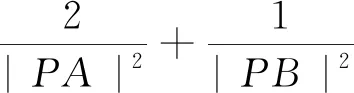
注：该法是化归为函数最值问题。

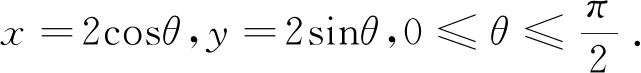
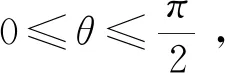
|PA|2=(2cosθ+2)2+(2sinθ)2=8(cosθ+1)

|PB|2=(2cosθ-4)2+(2sinθ)2=4(5-4cosθ)所以有

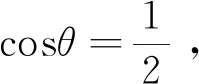
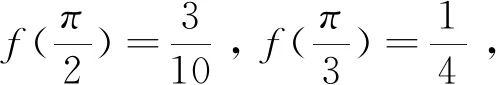
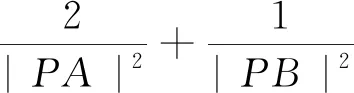
注：该法是利用圆的参数方程，再化归所求问题为含三角函数的函数的最值问题。

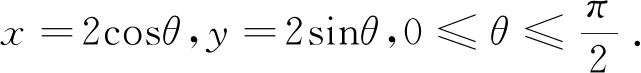
|PA|2=(2cosθ+2)2+(2sinθ)2=8(cosθ+1)

|PB|2=(2cosθ-4)2+(2sinθ)2=4(5-4cosθ)

所以有

令u=16cosθ+16,v=20-16cosθ，则有

u+v=36.

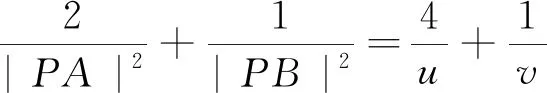
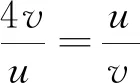
u=24,v=12.

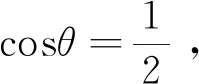
注：该法是利用圆的参数方程，再把所求问题化归为均值不等式求最值问题。

虽然题目涉及直线与圆，是解析几何学习的基础，但是不能就认为其简单。因为直线方程的选取可以是几种形式之一，圆的方程也可以是几种形式之一，不同选取的组合会产生其它不同解答过程(在此略去)。

另外，在第二问解答中出现一些考生对

连续作两次均值不等式，在第二次时断定PA=PB时取得最小值。尽管结果会正确，但其解法有缺陷。原因是两次均值不等式取等号的条件不同，仅用第二次取等号得出结论，需要证明没有逾越第一次均值不等式成立的范围。

3 关于高中解析几何教学的几点建议

高中解析几何主要内容是将直线、圆、椭圆、双曲线和抛物线这五种曲线在合适的平面直角坐标系下转化为二元一次方程(仅直线)或二元二次方程，然后通过研究方程(组)来研究曲线等具有的性质和关系。因为代数化以后，距离、夹角、面积和平行、垂直、相切以及弦长等问题都可以通过涉及方程系数的相关计算进行。不仅由于各种曲线的方程表示有几种情形，导致解决问题在选择上不一定唯一，从而体现灵活性，而且由于平面几何中计算和证明问题涉及较多点，如距离、面积和夹角等，从而容易与纯几何、函数、三角等内容综合考查。因此是考核综合分析解决问题能力的重要内容之一。

(1)重视平面几何的基本知识的几何集合表述到代数表述的理解与训练，增强学生从几何到代数的建模思想方法和能力。

建议从平面直角坐标系针对点与有序数对的一一对应开始使学生建立形与数的对应方法。 然后针对五种曲线(除直线外)定义出发建立方程的思想方法。这样重点培养由形到数(方程或方程组)的几何问题之代数表示思想方法。

(2)在建立曲线的代数表示(方程)后，强化如何利用方程的系数研究平行、垂直、相切和相交关系以及距离、夹角、弦长等计算方法与分析能力。

建议以直线和圆的相关内容为该要点的基础，避免许多教师和学生误以为此部分属于比较简单的知识。然后以圆锥曲线部分为强化与提高。重视思维误区点的点拨，一般方法与特殊情况的不同对待，综合问题的拆分与组合等训练与强化。

(3)对综合问题要恰当分类对待，如直线与二次曲线相切、相交中的问题以及分类，以便清楚常规类型和常规方法的深刻理解与应用。

建议从直线与圆的三种关系开始，重点突出常规方法，如德尔塔法和距离法等，强调在方程、方法、关系等选取上的不同会导致各种不同的求解过程，培养发散的灵活的思维能力。在教授圆锥曲线与直线关系时，先在直线与椭圆的关系和圆与直线的关系的比较上下功夫，再研究双曲线和抛物线与直线的关系处理的不同和相同之处。在“定”与“变”问题上下苦功夫。具体教学理论、策略和方法等可参考文献[1-4]。