血栓非线性黏度性质研究
2020-08-20高彭松刚芹果王光磊王洪瑞王中阳
高彭松, 李 艳, 刚芹果, 王光磊, 王洪瑞, 王中阳
随着人们生活水平提高,心脑血管疾病更为多发,成为引发其他各种疾病甚至死亡的常见疾病[1]。血栓是各类心脑血管疾病一大诱因[2],常见治疗方法包括抗凝药物、手术取栓及系统溶栓。介入技术发展,使得导管直接插入血栓溶栓普遍推广。然而介入取栓过程中血栓离析和重新凝结会导致患者突然死亡,这与其生物力学特性,尤其是流变学性质有着紧密联系[3]。近年许多学者对血栓进行研究,主要通过弹性实验、拉伸实验评价和比较血栓模型机械力学性能(回复度、最大拉伸长度),实验设计均从固体力学角度出发,相较于动态分析仪缺乏流变性质表述[4-7]。目前关于血栓流变性质研究相对较少。李元杰等[8]在血液和斑块等与血栓组织成分或环境相近流变学研究中发现,血栓形成与血液黏度有着紧密联系,认为血液黏度超过某一临界值时血栓会首先在管壁附近形成,血黏度低于临界值时血栓能逐渐化解,以至消失。李志勇[9]同样研究发现,血管在斑块生长过程中会逐渐狭窄,斑块因此处于高剪切环境,但斑块如何生长成为易损斑块和斑块最终如何破裂的生物力学机理尚不清楚。本研究在上述研究基础上,结合真实数据,分析血栓黏度随剪切速率变化的关系,并与已知流体黏度模型作对比,选择出拟合效果更好的模型,同时讨论方程模型中的某些参数,以此研究血栓流变行为。
1 材料与方法
1.1 临床资料与实验器材
2017年6月至2019年4月,与河北大学附属医院介入血管外科医师合作,获取8例患者手术取栓后离体1 h真实血栓样本(图1)。其中男7例,女1 例,年龄为 51~65 岁,平均(59.2±4.5)岁;发病时间 3~10 h,平均(5.8±2.4) h;病灶部位:左侧颈动脉3例、右侧颈动脉1例、左侧大脑中动脉1例、右侧大脑中动脉2例、基底动脉远端1例。实验仪器包括MCR301型旋转式流变仪(奥地利Anton Paar公司)、DC-2006型恒温水浴箱(上海舜宇恒平科学仪器公司)、BEKO系列空气压缩机(德国BEKO公司);实验试剂包括无水乙醇、4%甲醛溶液。

图1 临床获取血栓实物
1.2 流变性测试
将血栓样本从4%甲醛溶液中取出,置于旋转式流变仪检测平台上。选择直径为25 mm CP-25锥板作为测试转子;启动流变仪和测试程序,设置实验温度为37℃,对血栓进行速率-黏度扫描。设定剪切速率变化范围自1 s-1至100 s-1,取线性变化,每个样本重复5次实验,每次实验间隔30 min,得到血栓黏度随剪切速率变化的关系。
2 结果
实验获得血栓在温度为37℃时、剪切速率自1 s-1至100 s-1变化下的黏度曲线,不同血栓样本黏度虽有所差异,但整体变化规律基本一致。以血栓样本1共5次实验曲线为例(图2,为使曲线图更加清晰直观,纵轴刻度按照对数规律变化),由图可知血栓黏度随剪切速率增加而降低,黏度在剪切速率为10 s-1左右时下降幅度最大,在较高剪切速率范围内下降趋势较为缓和,总体表现为剪切变稀的假塑性流体;血栓黏度同时受到实验次数的影响,随着实验次数增加而逐步下降,曲线走势基本不随实验次数增加而变化。Surendra[10]在生物流体力学研究中指出,血液可被认为是幂律流体或Herschel-Bulkley流体;以此为基础,为进一步描述血栓黏度-剪切速率流变曲线,考虑应用描述假塑性流体黏度的常用模型幂律方程和Herschel-Bulkley方程。
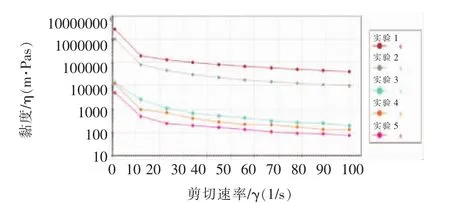
图2 血栓黏度-剪切速率曲线
2.1 模型选择
幂律方程是目前在工业领域应用最多的黏度模型方程,其表达式为:

若改写成应力-剪切速率方程,则为:

式中η为黏度,γ˙为剪切速率,K为黏度指数(K值越大说明样本黏度越高),τ为剪切应力,n为样本非牛顿指数。材料为假塑性流体时n<1,且材料假塑性越强,n偏离1程度越大。在γ˙一定变化范围内,K和n可视为常数。取每个样本第1次实验数据,得到拟合结果见表1。

表1 幂律方程拟合血栓样本实验数据所得参数
结合图2和表1拟合结果,发现幂律方程所得拟合曲线相关系数R2平均值为 0.922 0±0.011,说明拟合度一般(R2值越接近1,拟合效果越好),同时K值偏大,带来误差也较大。这种误差在剪切速率较低范围内尤为明显,这是由于幂律方程仅适合描述屈服应力很小且流变行为无依时性的物质[11],在物质处于很高(趋于无穷)或很低(趋于0)剪切速率时无法较准确地描述其流变性质。若观察幂律方程的应力-剪切速率本构方程,即公式(2),其应力在极低剪切速率段理论上应趋于0;而实际实验中可测得血栓在剪切速率趋于0时仍存在较大剪切应力,如表2。由此可认为,血栓流变学黏度性质中存在较大初始屈服应力,同时为了提高拟合精度,考虑应用带有初始屈服应力参数的Herschel-Bulkley黏度方程进行拟合。
Herschel-Bulkley黏度模型方程基本形式为:

若改写成应力-剪切速率方程,则为:

式中τ0为初始屈服应力。与幂律方程相比,Herschel-Bulkley方程多了初始屈服应力这一参数,其物理意义为流体仅在受力大于初始屈服应力时才会流动,受力小于初始屈服应力时流体剪切速率为0[12]。单次实验过程中,初始屈服应力可视为常数,数值大小可取表2中数据,取每个样本第1次实验数据,得到拟合结果见表3。对比幂律方程与Herschel-Bulkley方程对同一次实验拟合结果,可知Herschel-Bulkley方程有着更好的拟合精度,R2平均值为0.997±0.007,本构方程中参数设置也能更好地解释实验现象;不同血栓样本因其内部组成成分不同,初始屈服应力和黏度指数差异较大,两种方程拟合得出的K值与n值也有一定差异,但总体趋势相同,可以说明Herschel-Bulkley方程更适合描述血栓的流变行为。
2.2 初始屈服应力分析
Herschel-Bulkley方程中初始屈服应力通常被认为是一定值常数,在部分血栓样本中数值较大。观察图2可发现,血栓黏度会随实验次数增加而减小,若对重复实验数据选用初次测量的初始屈服应力进行拟合,则会导致方程(3)中第1项过大而无法对黏度作准确描述。现定义每个样本第1次实验所得初始屈服应力为τ0,后续实验中初始屈服应力为τ0'。实际上,罗静等[13]在材料流变学研究中就提出流体初始屈服应力大小会因添加剂多少和温度高低而改变。由于血栓特殊性,研究其力学行为需要在近似人体体温环境下进行,血栓组织中也不含添加剂成分。因此,可将后续每次实验中的τ0'视为随实验次数(N)和第一次实验得到的τ0而变化的函数,即τ0'=(N, τ0)。 图3为8例血栓样本分别在5次实验中初始屈服应力随实验次数变化的Matlab拟合曲线。

表2 剪切速率趋于0时不同血栓样本剪切应力

表3 Herschel-Bulkley方程拟合血栓样本实验数据所得参数
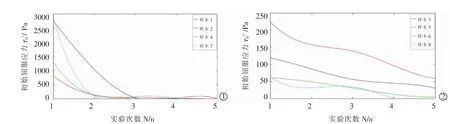
图3 血栓初始屈服应力-实验次数曲线
8例血栓样本的τ0'随实验次数下降表现出两种不同趋势,图3①中4例样本第1次实验得到的τ0虽有一定差别,但数值均较大,意味着样本本身黏度较大,仅在受到较大应力时才会流动,变化曲线体现出很强的非线性;图3②中4例样本τ0均较小,说明样本本身黏度较小,随实验次数变化规律接近于线性。总体上,随着实验次数增加,血栓样本内部流变性质均发生一定程度变化,即使在放置一段时间后也未完全恢复。τ0值大小可在一定程度上反映不同血栓样本内部成分的差异,影响后续实验中τ0'随实验次数变化的规律。若取初次实验与末次实验数据点对曲线作割线,所得割线斜率如下表4。割线斜率反映样本初始屈服应力随实验次数增加的变化速度,可看出8例样本曲线割线斜率大小基本可划分为两种状况。图3①中4例样本τ0均大于500 Pa,割线斜率值较高且相互差值较大;图3②中4例样本τ0均小于500 Pa,割线斜率值较低且较为集中,τ0具体数值可参见表2。

表4 血栓初始屈服应力-实验次数曲线割线斜率
根据现有样本,可初步以τ0=500 Pa为界限,推测τ0>500 Pa样本中不含钙化成分,变化规律如图3①,τ0≤500 Pa样本中含有钙化成分,变化规律如图 3②。 对于 τ0较大的血栓样本,如样本 1、2、4、7,前2次实验对血栓流变属性影响较大,实验次数>3后τ0'基本可视为随实验次数线性下降。5次试验后8例样本τ0'均已接近于0,即黏度也是以极低数值在很小范围内变化。根据已有样本实验数据对两种不同试验情况进行拟合,得出τ0'=(N,τ0)函数如下:
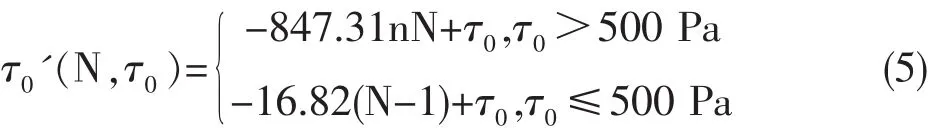
3 讨论
为了定量研究血栓流变学黏度特性,本研究应用旋转式流变仪测定了血栓样本在不同剪切速率下的黏度数值,并将实验数据输入Matlab拟合工具CFtool中,评价与选择合适的黏度模型对血栓流变行为进行描述。结果发现血栓是典型的剪切变稀的假塑性流体,与幂律方程相比,应用Herschel-Bulkley方程获得的血栓黏度-剪切速率拟合曲线拟合精度更高,方程中参数τ0设置也更贴合血栓流变学黏度特性。为了更好地解释重复实验中血栓样本黏度下降现象,对Herschel-Bulkley方程中τ0参数又进行讨论,分析不同种类血栓初始屈服应力的变化规律,以τ0=500 Pa为指标对血栓种类进行初步划分,并给出数学模型。该模型能够为临床上腔内介入取栓提供一定的生物力学依据。
本研究主要根据真实血栓实验数据在数值上分析血栓流变学黏性行为,然而对于一些数值差异难以给出准确的基于病理学的解释。血栓中有无钙化成分、是否存在炎症,均会影响其黏度及初始屈服应力,不同患者个体差异性也会导致血栓流变行为有所改变,如何精确建立分类标准还需要积累更多样本。此外,若按组织成分划分血栓类型,总体上可分为红色血栓和白色血栓两大类,不同血栓类型决定了不同治疗措施[14],如何根据血栓黏度性质确定其内部成分还有待进一步研究。
