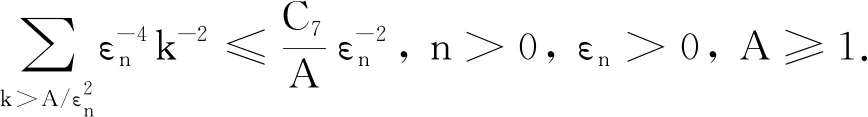基于临界Galton-Watson过程的随机游动的大偏差

杨旭， 国洪松

( 中国矿业大学(北京) 理学院， 北京 100083 )

0 引言

(1)

依照文献[5]中的方法，很容易验证Rn的正态大偏差概率为

(2)

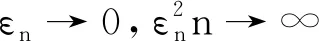
1 相关假设及引理

1.1 基本假设

1.2 相关结果

引理1[4](Fuk -Nagaev不等式) 对k≥1,εn>0,n≥1,r>1, 有

引理2[6](基本引理) 如果m=ΕZ1=1，ξ2=VarZ1<∞， 那么在0≤t<1上一致有

其中fn(t)为矩母函数f(t)的n次迭代.

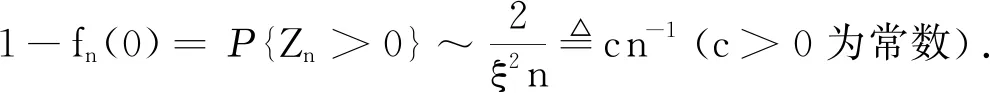
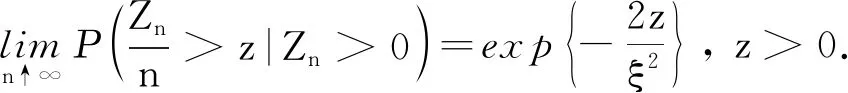
定理2[7]令ξ2<∞，k和n的比值k/n以有界的方式趋于无穷，那么有

其中d为{pk;k≥0}的最大公约数.

2 主要结论及其证明

定理3假设Z是临界 Galton -Watson过程，m=1，ξ2=VarZ1∈(0,∞)， 则根据式(2)有

(3)

证明根据全概率公式知，对∀δ∈(0,1)和1

以下分3部分证明定理3.

(a)根据引理3， 对∀k，n≥1, 有

(4)

(5)

(6)

综上所述，定理3证毕.

证明根据全概率公式知，对∀δ∈(0,1)和1

下面分3部分证明定理4.