基于神经网络的厚壁深裂纹定量检测方法
2020-08-19姜禄张东利王闯龙佟宇
姜禄,张东利,王闯龙,佟宇
(1 北方民族大学电气信息工程学院,宁夏 银川 750021;2 北方民族大学机电工程学院,宁夏 银川 750021)
在航空航天、能源核电等重要领域,为保障设备正常使用,要求对关键零部件的表面和内部深层都进行缺陷检测。目前,常用的检测方法有超声、射线、涡流等,其中,超声检测过程中需要用到耦合剂并且检测过程易受外界因素干扰,无法实现高效的快速检测[1],射线法由于有一定的辐射,只能在特定场合使用,这使得其在工程实践中受到很大限制[2],涡流检测对环境要求低且检测数据易于被数字化处理,使其被广泛应用[3-4]于金属材料检测,但在检测较深裂纹时,裂纹深度越大涡流检测信号敏感性越低,这使得深裂纹的反演定量较为困难。常用反演定量方法有标样法、优化法、神经网络等,其中,标样法只适用于缺陷形状已知的定量检测,对复杂缺陷的定量较困难;优化法在优化过程中需要根据正演问题模型反复迭代计算,计算量大且对计算环境要求较高;神经网络结构简单、包容性强、求解速度快,其被广泛应用于检测领域[5-7]。彭国平等[8]对自制不锈钢试件进行涡流检测,通过对比信号差异的方式检测出缺陷,从而证实了涡流检测对非铁磁性材料表面裂纹检测的可行性;黄凤英[9]对钢轨表面5 mm以内裂纹进行涡流检测,利用拟合的指数函数式对缺陷进行评估,结果表明对2 mm以内裂纹定量检测效果较好,裂纹深度超过2 mm时定量评估误差会大于10%;梁远远[10]利用新型探头对2 mm以内缺陷进行检测,以BP神经网络对缺陷进行定量评估,定量效果较好,相对误差平均值为4%。
综上所述,目前对5 mm以下浅表裂纹的检测及定量效果较好且研究较多,而工程实践中5 mm以上缺陷大量存在,所以对深裂纹进行定量研究具有工程实际意义。本文研究采用神经网络的方式对5 mm以上深裂纹的涡流检测信号进行训练,以期提高其定量检测的精度。先采用有限元软件ANSYS对深层缺陷进行涡流检测过程仿真[14-17],获得不同深度裂纹阻抗信号,再优化网络输入层结构,采用小波多分辨率分解的方式对阻抗信号进行预处理,从而降低数据冗余性,并通过优化神经网络的结构降低神经网络隐含层对识别精度的影响,最后利用实验测得的深裂纹阻抗信号验证该方法在深裂纹定量识别上的可行性与准确性。
1 不同深度裂纹的阻抗信号仿真
在涡流检测过程中,裂纹对检测信号的敏感性随检测深度的增加而降低。为使检测深度达到15 mm,依据标准渗透深度公式,通过计算决定采用频率为5 kHz的低频涡流信号对其进行检测。为了得到深裂纹的仿真检测数据,本文利用有限元软件ANSYS对涡流检测过程进行仿真,仿真过程中采用自发自收式圆形线圈对深裂纹进行检测,使用的线圈参数见表1。

表1 线圈计算参数
仿真过程中被检试件使用材料为304不锈钢,尺寸大小为40 mm×25 mm×20 mm,其属性参数见表2。由于后续实验中加工的深裂纹为人工通槽,所以仿真中裂纹的属性采用表2中空气的属性参数,形状是宽度为0.2 mm的通槽,仿真试件、探头位置和扫查方向见图1。

表2 材料属性

图1 试件和探头放置位置
使用上述模型对5.00~15.00 mm(间隔0.01 mm)深度的裂纹进行涡流仿真计算。各深度裂纹分别进行3次仿真取平均值处理,以减少计算误差,共得到1 000组有效数据,其中部分裂纹在仿真下得到的阻抗模值数据见图2。由图2可以看出:随着裂纹深度的增加,阻抗数据的幅值也增加,说明二者存在一定的映射关系,同时,随着裂纹深度增加,阻抗数据模值的增量随之减小,这一点符合检测灵敏性随裂纹深度增加而降低的特性。

图2 部分深度裂纹阻抗仿真计算结果
2 基于神经网络的深裂纹定量识别结果
本文采用单隐含层神经网络对深裂纹进行反演定量识别,图3为其结构拓扑图,其中各层之间为全连接,即在一次前向迭代中计算次数为各层节点数的乘积,其结构复杂性主要取决于输入节点和隐含层节点数量的多少。
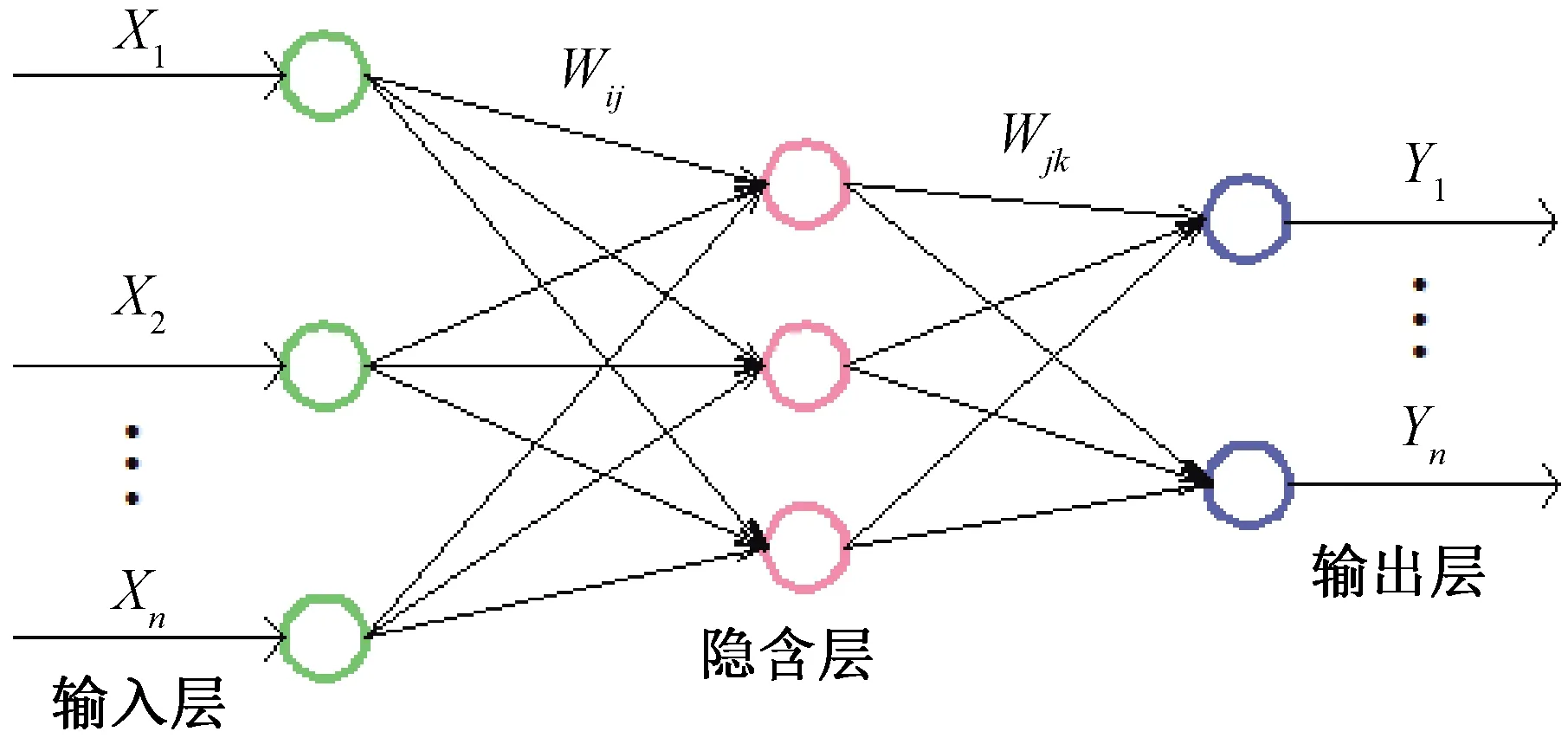
图3 神经网络拓扑图
由于检测得到的数据很多,若直接以检测得到的数据作为神经网络输入,会导致网络产生过拟合的现象,使裂纹反演定量精度变差,所以降低网络输入结构复杂性和数据冗余性非常必要。针对这一问题,本文利用小波多分辨率分解对深裂纹的阻抗信号进行优化处理,以处理后的某层信号极值作为输入,以达到降低输入数据冗余性和简化神经网络输入节点的目的。
神经网络隐含层节点个数的选择会影响最终的反演精度,因此,确定最合适的隐含层节点个数非常必要。本文首先通过经验公式计算出隐含层取值的范围,之后再固定输入层和输出层的个数,在取值范围内多次取值进行计算,以深裂纹识别值相对误差最小为依据,最终确定最优隐含层节点数。
2.1 神经网络输入层结构优化
过多的数据量将产生较大的数据冗余性,为降低数据冗余性需要简化神经网络输入层节点结构。本文研究利用小波多分辨率分解对裂纹检测信号进行提取特征值处理,以8 mm裂纹在涡流检测仿真下得到数据为例,以db5为小波基对仿真得到的阻抗信号进行三层分解,得到4个频率级,结果见图4。

图4 小波多分辨率分解结果
其余各组数据做相同处理,统计各裂纹分解后结果得出:原数据进行分解后,第1层细节信号极大值为3个,第2层细节信号极大值为1或2个,第3层近似信号极大值为1个。为保证神经网络输入节点数结构具有一致性且具有较高辨识性,选用第1层细节信号的极大值(表3)作为神经网络的输入。

表3 部分深裂纹阻抗经小波变换后第1层细节信号极大值
2.2 神经网络隐含层结构优化和识别结果
神经网络隐含层节点数由以下3个相互独立的经验公式确定:
l (1) (2) l=log2n, (3) 其中,n为输入层节点数,l为隐含层节点数,m为输出层节点数,a是1~10之间的常数。 为得到最优网络结构获得最佳裂纹识别准确率,通过上述3个公式计算得到范围取并集和隐含层节点数l∈[2,12]。 本文以裂纹识别准确率相对误差最小为依据,相对误差=|(真实值-预测值)|/真实值,用优化处理后的随机950组数据作为网络训练样本,其余50组数据为测试样本,在3-l-1网络结构下对裂纹深度进行定量识别。识别结果(表4)表明:3-6-1网络结构下裂纹深度识别值的相对误差平均值最小为0.626 5%,识别准确率最高。 表4 隐含层取值对裂纹深度定量识别结果的影响 本文利用ANSYS对深裂纹进行涡流检测过程仿真,以db5为小波基对得到的检测数据进行三层分解,利用第1层细节信号的极大值作为神经网络输入,以3-6-1网络结构对其进行裂纹的定量识别,识别相对误差为0.626 5%,表明此方法对深度裂纹定量识别有效,识别准确率较高。 上述结果为仿真计算所得,为验证此方法在实际中的有效性,还需进行实验验证。 设计加工(仅部分裂纹)SUS304不锈钢试件(图5),其尺寸为1 350 mm×350 mm×20 mm,电导率为σ=1.43×10-6S/m,相对磁导率为ur=1。裂纹为不锈钢试件上均匀加工的人工通槽,宽度均为0.2 mm,深度分别为5、7、10、13、15 mm。 图5 部分不锈钢试件 为了减少实验操作造成的误差,将检测线圈和激励线圈安装在三维扫查台,保持恒定速度在不锈钢试件上表面进行扫描;使用爱德森涡流检测仪作为采集系统,常规圆形涡流探头作为采集端和激励端(图6)。 图6 实验装置位置 实验使用的激励线圈内径为8 mm,外径为15 mm,激励频率f为5 kHz,提离d为0.5 mm,匝数n为140匝。实验结果(图7)显示:涡流检测得到的阻抗数据的幅值随裂纹深度的加深而增加,与仿真中阻抗数据幅值与裂纹深度的关系一致。 图7 不同裂纹阻抗的实验结果 采用仿真过程中的处理方法,以db5为小波基对实验得到的阻抗数据进行三层分解,提取第1层细节信号极大值作为神经网络输入。由于试件有限共得到5组数据,将其中三组为训练数据,另二组为检测数据,用3-6-1网络结构对裂纹深度进行定量识别,识别结果(表5)表明,识别值的相对误差较大。对比仿真过程及结果分析其原因为实验数据较少,网络训练不充分,偶然性较大。 表5 裂纹深度定量识别结果 裂纹深度增加时阻抗幅值也增加,说明二者之间存在一定的映射关系,因此,对其进行以下增量处理:在图7数据的基础上,在同一检测位置以不同裂纹深度值为自变量,其对应的裂纹阻抗幅值为因变量,利用三次样条插值原理对其进行插值增量,增量至1 000组数据,用其中950组数据为训练样本,剩余50组为检测样本。重复上述定量过程,识别结果见图8,经统计表明:深裂纹识别值的相对误差最大值在5%左右,相对误差平均值为2%左右。 图8 不同裂纹深度识别结果 本文对实验数据与仿真数据进行相同处理,都得到较高的裂纹识别准确率,二者识别精度虽略有不同,但都在误差允许范围内,说明本文提出的基于神经网络的定量识别方法对深裂纹可以进行有效定量识别,且精度较高。 本文使用有限元软件ANSYS仿真涡流检测过程及对深裂纹定量反演的方法可对深裂纹进行有效的定量检测,定量识别的准确率约为98%。这种方法可为深裂纹的定量检测提供参考,为确保机械设备安全运行提供可靠依据。
3 深裂纹定量结果实验验证
3.1 实验验证


3.2 实验结果与分析



4 结论
