电缆防护层故障点的红外立体视觉检测

程羽佳，杨晴，王凡

（电子科技大学中山学院机电工程学院，中山 528400）

0 引言

对于电力系统来说，输电稳定性至关重要，有了稳定的电能输送，电力设备的工作效率才能得到最大程度的保证。作为电能输送的载体，高压电缆防护层需要保证良好的绝缘状态。因为在现代电能输送过程中，高压、超高压输电已经成为常态。若电缆防护层被击穿破损，则会造成难以想象的后果。严重的，甚至会带来人员的安全隐患。

电缆与普通的电气设备不同，其安装位置较高。同时，经过不断地绝缘技术改良，其温度变化的趋势较小。因此，在普通的电气检测过程中，电缆的工作状态检测难度较大。若发热的异常点长期存在，经过积累，会造成绝缘材料的击穿。此时虽然发生了故障，但击穿点较小，同样难以精准定位，造成检修的困难。常用的方法是基于表面颜色变化或采用点温仪对电缆防护层进行测量，但是测量的精度得不到保证，存在较大的安全隐患[3-4]。另外，可以使用红外检测技术来进行测量，这种方法的优点主要体现在以下两点：

（1）红外检测技术属于无损检测，不会损坏电缆表面。同时，非接触式的测量，可以最大程度地保障测量人员的人身安全。

（2）相对于人眼识别或者传统的点温仪检测方法来说，红外检测技术的精度较高。由于点温仪属于发散检测，而电缆架设较高，测量距离相对较远，则误差更大。实验表明，点温仪对于电缆绝缘材料温度的检测误差达到5～10℃。而通过人眼观测表面形态或颜色变化来确定温度异常点的方法，其测量结果更是无法保证精度。而红外立体视觉检测技术发展迅速，能够很好地反应电缆表面温度，测量精度较高。

1 算法实现

1.1 红外电缆图像特征点提取

在红外图像处理的过程当中，首先要进行特征点的提取。因为图像中的信息较多，尤其在电缆红外检测中，被测对象所处环境复杂多样，为了排除干扰，需要滤除不必要的信息。特征点的提取方法较多，根据实际需要，红外电缆图像检测特征点的提取采用SIFT算法。其特征尺度由可变高斯函数结合二维图像信息组成[5]，如式（1）所示。

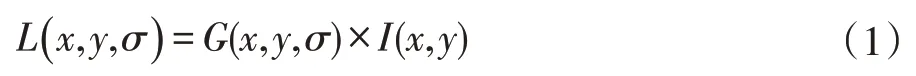
式1 中，I(x,y)包含的是二维图像信息，而G(x,y,σ)为可变高斯函数，经过相应的运算，可以转化成式（2）。

上式中，（x,y）表示的是二维图像坐标，σ表示尺度因子。首先，利用高斯函数，搭建相应的DOG 模型，每个模型对应一个图像特征点，此模型的形式与金字塔结构类似。对每一个模型进行极值点的检测，从而确定每一个特征点的具体坐标信息。

在DOG 模型中直接取值会导致计算误差变大[6]。因为利用SIFT 算法进行特征点检测，其核心为区域检测，即以固定区域的中心作为特征点，所以存在一定的误差，需要对DOG 模型搜索到的数据进行二次检测，从而确定最终的特征点坐标。对测量的特征点数据进行插值运算，并通过3D 二次方程进行处理。空间尺度函数假设为D(x,y,σ)，经过特征点拟合后，其泰勒展开式可由式（3）表示：

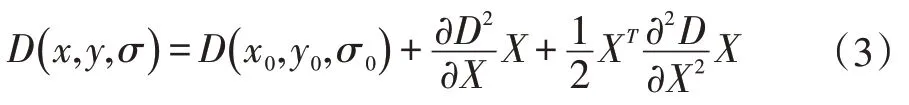
上式中，通过相应的差分运算，可以求得空间尺度函数的二阶导数。在此基础上，通过式（4）重复进行二阶求导，同时设改值为0，可以求取精确的极值Xmax。

为了提升后续的图像匹配效果，在特征点提取的过程中，需要把干扰噪声点消除。所以。匹配不佳的特征点需要从结果中筛除。式（3）和式（4）联立方程组，得到式（5）。特征点筛除需要选择一个临界值，经过实验研究，临界值选择 0.03 效果最好，即特征点若符合此条件，该点保留，继续参与后续处理过程。若不符合，则删除。

针对图像中一些已经选取的特征点，但其效果不是特别理想的，可以通过式（6）的Hessian 矩阵再次进行处理。该矩阵属于二阶矩阵，通过该矩阵可以把邻域差分法中计算出的每个特征点的偏导数，置于其各个分量中，矩阵如式（6）所示。该数据是通过近似估计求取。

每个特征点的主曲率都可以通过式（6）中的方阵H 求取。当矩阵中的特征值越大，则说明D（Xmax）的值也越大。因为两者成正比例关系，所以，只需把正比例系数ratio 求出即可，而不需要求取特征值的具体数字。设特征值的给定峰值为α，次峰值为β，两者的比值设置为P2j（x,y,z），则通过式（7）可以求取正比例系数ratio：

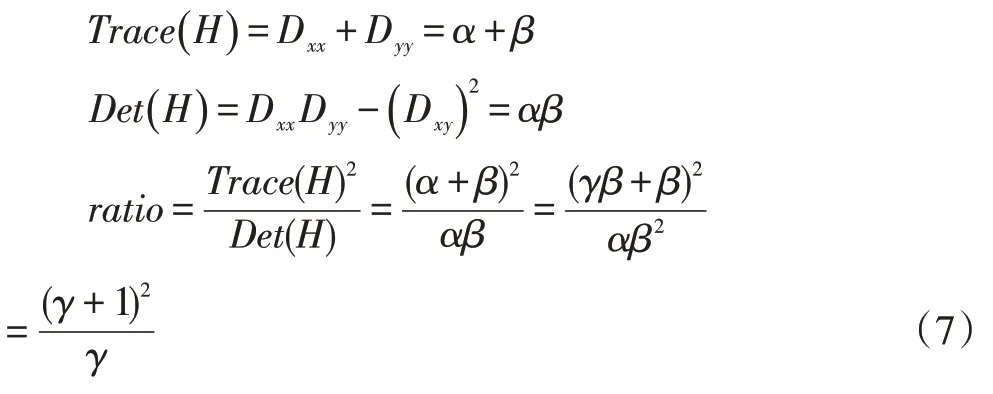
通过前期计算验证，当γ=10 时，检测效果较好，可以准确地获得特征点的具体坐标及其旋转角度。只要正比例系数满足式ratio≤(γ+1)2/γ即可。

1.2 特征点匹配

基于SIFT 算法进行红外图像特征点匹配的方式，属于特征匹配算法。即在进行特征点测量的同时，也在开展特征点匹配的工作。对每一个检测到的特征点，MATLAB 都会赋予其一个特定的标志。通过该标志，系统可以正确地识别每一个特征点。因此，匹配特征点的工作可以转化成匹配标志点的工作，标志点也可以被称作描述子。在进行SIFT 算法的特征点匹配过程中，若能准确地检测每个特征点的描述子，将会大大提高特征点匹配的精度。而对于描述子检测来说，如何对其进行优化和区分，是最为关键的步骤。

在描述子检测过程中，可以把每个特征点的位置坐标以特征向量的形式表现出来。在特征点发生移动的时候，特征向量也会随之改变。同时，在另外一种情况下，当有强烈光照时，特征向量不变。此特征与描述子的变化方式类似。所以，通过把特征点转化成特征向量，可以更好地检测描述子。同时也能满足对于特征点方向，旋转角度等信息的匹配。另外，对于特征点附近的微小区域，也进行相应的处理，使得特征点能够更加突出地显示。设特征点坐标为（x,y），每个特征点的梯度值及梯度方向都可以通过式（8）求取，即：

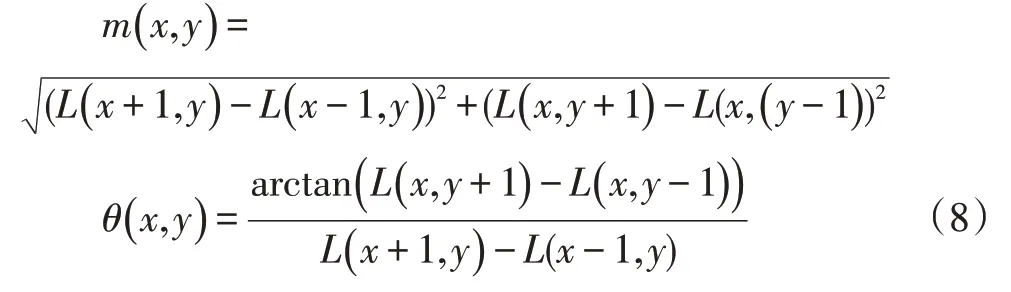
被测红外图像中，每个特征点的位置都不相同，通过式（8），把图像二维坐标（x，y）与该特征点的差异尺度L 相结合，可以求取每个特征点所对应的像素位置。

距离函数可以判断两幅特征点检测图像的对比度。对于两图的对比情况，本文选择距离函数进行评判。常用的距离函数有两种，分别是马氏距离与欧氏距离。其中，欧氏距离也被称作欧几里得度量。该方法在评判对比图像特征点直线距离方面精度较高，所以本文使用欧氏距离，评判红外检测图像的相似度对比。具体的实现原理是分别求取两对比图像特征点对之间的直线距离，然后对比两距离的长度，从而对两幅红外被测图像相似度做出判断。

通过欧氏距离进行处理后，两幅红外被测图像的特征点匹配工作便初步完成。为了更进一步提升特征点匹配的准确性，得到更好的立体匹配效果，可通过k-d tree 最近邻搜索法检测“叶结点”。具体过程是选择一个特征点，在该特征点附近搜索离其最近的另两个特征点并将其设置为“叶结点”，“叶结点”之间的直线距离作为最小距离。然后继续进行搜索，判断是否有另外的“叶结点”，其直线距离比最小距离更小。若没出现更小的距离，则判断两数据点可选；若出现更小的距离，则将该距离设置为新的最小距离，其对应的两数据点作为新的“叶结点”。

综上，在红外被测图像的匹配过程中，首先需要确定每个特征点所对应的描述子。然后，利用欧氏距离判断匹配图像对的相似度，并求取特征向量。最后，通过k-d tree 最近邻搜索方法对匹配结果进行检验。即将“叶结点”之间的最小距离作为检测距离进行搜索。如不存在更小的“叶结点”距离，则该特征点对匹配成功；若附近存在更小的直线距离，则有其作为新的最小距离，再次进行递归搜索。随着最小值的不断缩小和替换，特征点对的数量不断减少，但是特征点对的精确率不断提高。因为错误点对被不断地剔除。匹配效果更好。同时，引入极线对比校正方法，即通过极线对比，使得二维图像校正转换成一维校正，该方法程序简单，缩短计算时间。通过SIFT 算子对红外图像进行特征点匹配的工作过程总结如下：

（1）使用两台后外摄像机采集红外图像，选择背景效果良好的图像进行匹配；

（2）采取SIFT 算法进行特征点匹配；

（3）对图像特征点描述子进行检测，使用欧式距离判断两幅匹配的对比度，计算特征向量，完成初步匹配工作。

（4）采用k-d tree 最近邻域法进行“叶结点”距离的搜索，不断筛除错误的特征点匹配点对，提高红外图像匹配精度。

2 电缆故障点红外检测结果

对长段电缆分成两部分进行检测，经过特征点匹配后，进行拼接，特征点匹配效果如图1 所示：

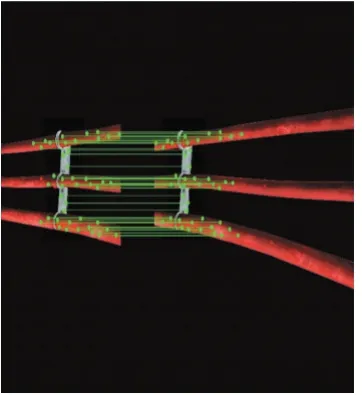
图1 两段电缆特征点匹配

从图1 可知，红外电缆拼接表面特征点提取准确，特征点匹配效果良好，能够较好地完成后续的图像处理工作。实验证明了拼接技术能较好地应用在大型高压电缆的红外检测当中。

在完成红外图像匹配及拼接处理后，发现每段电缆的红外图像都存在红色的异常点。此类异常点的产生是由于电缆在产期工作中，由于绝缘材料的损耗，产生了电树枝。并且造成热量的积累，若不能及时进行处理，排除故障，热量会急剧上升，造成热畸变甚至材料被击穿。通过MatLab 软件对此类红外图像异常点进行灰度处理，比较灰度值的变化，便可以正确提取发热异常点，如图2 所示：

图2 温度异常点检测

通过图像处理软件统计被测电缆红外图像温度异常点的数量和在电缆图像当中的比例，还可以判断该电缆绝缘材料性能的优劣。

3 结语

本文对电缆红外图像进行立体匹配的工作，从测量结果看出，特征点提取良好，匹配准确；同时，对长短红外电缆图像进行拼接，从拼接效果可以看出，拼接表面光滑，完整地反映了长段红外电缆的特征；最后，对红外电缆图像中的温度异常点进行提取，从温度异常点的数量及所占比例，判断电缆的工作情况。