证券投资个股风险的VaR值测算分析
2020-08-18杨可可
杨可可
(安徽大学经济学院 安徽 合肥 230601)
一、VaR基本理论概述
(一)VaR的概念及特点
VaR(Value at Risk),即风险价值度。通常解释为:VaR是在一定置信水平和一定持有期内,某一金融资产或组合在正常的市场条件下所面临的最大损失额。
具体含义为:在一定时间期间(T)内,我们有X%的把握,损失不会大于V。这里的V就是我们要求的风险价值度VaR。时间期间(T)和置信度(X)是构成VaR函数的两个基本要素。VaR就是在X%的情况下,T天持有期内可能导致的最大交易损失。
用数学的语言来表述为:Pr(ΔVΔt>VaR)=1-c,式中,ΔVΔt为资产或资产组合在拥有期间Δt内的亏损;VaR为置信水平c下处于风险中的价值。就数学统计上的含义看,VaR可解释为在一个既定的盈亏预期函数分布中,一定置信水平下的分位数。换句话说,VaR值计算的主要环节是确定资产未来盈亏的统计分布或概率密度函数。
由上可知,VaR方法之所以能够变为当今流行的风险测度方法,与其自身的特点息息相关:第一,VaR将一系列复杂的风险测度问题量化为具体一个数值,简单明了,不仅让投资者知道了发生损失的大小同时让投资者了解了发生损失的可能性;第二,VaR方法较其它方法更灵活,其可以选择不同的置信程度得到不同风险状况下的VaR值,针对性更强;第三,其说明的金融资产受整个市场风险的影响,更能反映市场价格的波动规律。
(二)VaR的计算原理和计算方法
VaR从根本上说是对投资组合价值波动的统计测量,所以求解它关键应是构建资产价值盈亏的数学分布,或者更准确来说是对反映投资组合变动的相关数学概率函数进行求解。它最基本的思想是运用单只证券或者投资组合历史价值的变化信息来对其未来的变动规律进行推测,与其他方法的不同之处在于其对将来价值变动的预估不是数值而是与其相关的概率函数。也就是说只要能较为精准的求出投资组合的概率函数,求出的与之相对应的VaR值也就比较准确。
因此,在求解VaR时,首先得到市场因子目前的价格水平,通过定价公式用每日结算的方式对资产的价值进行估计;此后是通过对市场因子将来价格水平的概率分布来对以上资产的价值进行重新估计,根据以上步骤我们可以得知资产价值变动具体值,同时也就得出了资产的盈亏分布;最后根据自身需求选择不同的置信程度和持有资产的时间长短得到资产的VaR值。
目前来说,计算VaR值的主要方法有三种:
(1)历史模拟法,此方法是将历史在未来可以重现作为假设前提,利用历史数据的分布函数来代表将来一段时间的收益率分布,此时VaR的估值就是对应的上面分布函数的收益率。
(2)蒙特卡罗模拟法,其原理是先将利用计算机产生大量随机数,再通过模型模拟收益率的不同分布对整体分布进行推测,也就是通过特定的随机过程反复拟合得到最后的收益率分布,从而依此计算VaR值。
(3)方差-协方差法,又称模型构建法,它是一种局部估值法。此方法原理在于先假定所要考虑的市场因子服从于一种数学分布,例如常见的正态分布和泊松分布,此后结合历史数据样本估算分布的相关参数,最后在给定置信水平和持有期的前提下快速求解得到VaR值。
方差-协方差法最显著的优势在于求解效率高且能够很好的刻画金融资产的时间序列特征,他能够简化VaR计算的主要原因是应用了数学上的概率统计原理。这种方法考虑到了多种风险因子,理论上适合对我国股市上的股票进行研究分析。因此本文选用方差-协方差法对单只股票进行计量研究。
值得注意的是,方差-协方差法理论基础是金融资产价值变动服从标准正态分布,根据大量的实证研究发现,我国股市股票价值历史分布较正态分布有较大的出入,其呈现尖峰厚尾的特征,那么如果继续采用这种方法,求解的VaR值就会因为不符合原假设而低于实际值。基于此,Bollrslev提出了GARCH模型,即通过建立GARCH模型来解决历史数据时间序列上波动聚集的特点,以此来增加对数据分布特征的描述的准确性,同时VaR值得求解也更精准。
二、VaR值测算实证分析
(一)数据的选取与预处理
实证研究对象的选取是整个分析的基础,本文选取恒生电子(600570)这支股票收盘价作为研究对象来对计算其以日为期限的VaR值。样本数据日期从2017年1月9日到2020年1月9日总计731个有效数据,对于数据的研究处理采用易于处理得对数收益率方法,具体计算公式为:Rt=ln(Pt/Pt-1),公式里Rt表示每日的股票收益率,Pt表示恒生电子的每天收盘价。在Eviews 10中键入公式R=dlog(P)对收盘价P进行求其对数收益率并差分R,从而得到730个对数收益率数据,也就是收益率时间序列。
(二)正态性检验
对恒生电子收益率时间序列的正态性检验过程是利用Eviews 10进行,检验结果如下:Mean为0.000766,Kurtosis为8.773035,Skewness为-0.494463,Jarque-Bera为1043.471,Probability为0。
从检验结果中可知,样本峰值8.773035比正态分布的峰值3略大,偏度S是-0.494463小于0,因此不符合正态分布,另外注意到J.B.值较大是1043.471,对应的p值为0,进一步说明样本期间内恒生电子对数收益率时间序列不满足严格正态分布的特点,从图中我们又能发现其收益率呈现尖峰厚尾分布的特点,由此开始思考利用建立GARCH模型来求解VaR值。
(三)平稳性检验
我们在建立模型时首先要保证收益率序列是平稳序列,因此必须检验恒生电子对数收益率的平稳性。本文运用Eviews 10软件对时间序列进行ADF检验,如果求解的ADF绝对值比标准值大时,则认定此序列是没有单位根,说明序列平稳,反之则不成立,具体结果为:Augmented Dickey-Fuller test statistic(ADF)为-26.31777;1% level检验结果为-3.439093;5% level检验结果为-2.865289;10%检验结果为-2.568822。
从检验结果我们得知,ADF的值是-26.31777,其绝对值与三个不同水平下的临界值进行比较结果是均略大,并且ADF检验结果是P为0,基于此我们可以认定恒生电子的对数收益率在此期间是平稳的。
(四)自相关性检验
由于做传统回归模型要保证随机误差项必须没有自相关性,以提高求解结果的准确性。本文对以上时间序列的自相关性的检验同样利用Eviews 10软件进行,具体结果如图1所示。
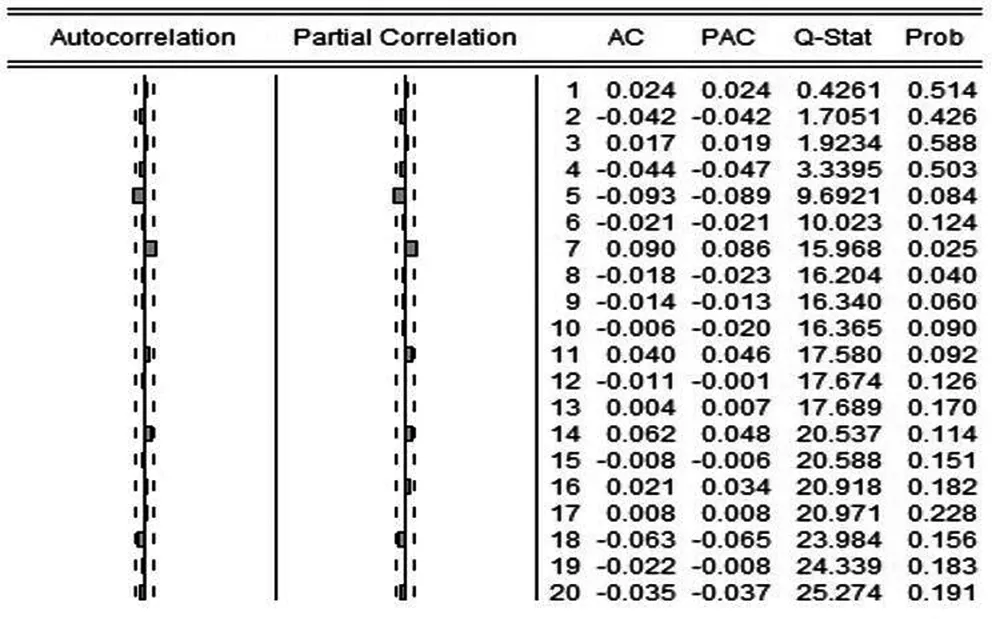
图1 样本数据的自相关性检验
在图1检验数据中,AC和PAC分别表示的是序列自相关值和偏自相关值,通过检验数据可知,两者的检验值都在零的左右徘徊并且都没有超过直方图虚线区域;再就Q值检验结果而言,都比要求的显著性标准值要小,另外P值检验结果也是较显著性标准略大,基于以上结果可知无自相关性的假设成立,因而本文认定恒生电子收益率时间序列之间的自相关性较弱并不影响模型建立。但是就检验结果而言残差序列明显有高阶的ARCH效应,此时,建立GARCH模型可以更方便描述这一过程。所以,我们下文选用GARCH(1,1)模型。
(五)GARCH模型的估计
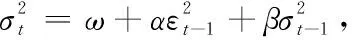
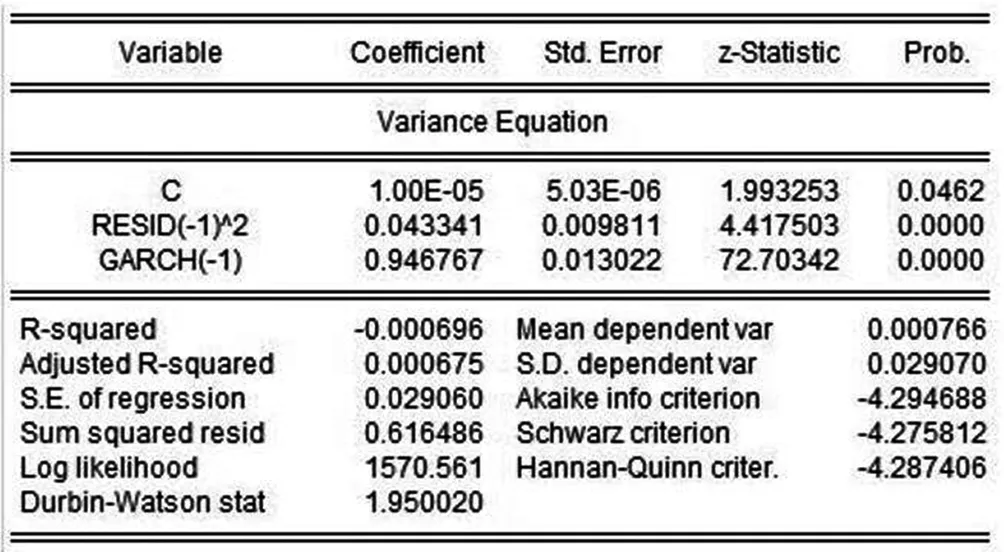
图2 GARCH(1,1)模型估计
通过估计结果得知,上面公式中的ω就是结果中的C值,0.04334对应的是式中的回报系数α,小于0.25,0.9467对应的是式中的滞后系数β值大于0.7。计算可知α+β<1但是却和1相差无几,D.W值是1.95约等于2,基于此我们得知残差序列的自相关性为零。另外,通过观察AIC和SC的检验值可知,二者皆为负数,表明建立的模型精简度符合要求。总体来说,建立GARCH模型估计结果理想。
(六)VaR值的计算
根据以上建立的的模型GARCH(1,1)参数估计结果,建立如下方程:
同时在Eviews10.0中导出GARCH方差序列,再开根号后就是σt的值,最后根据公式:VaR=Pt-1Zασt,可求出VaR值,其中Zα为置信度,在95%的置信度下Zα的值为1.645,在99%的置信度下Zα的值为2.33,根据投资者风险偏好的不同就可以选择不同的置信度进行计算,最终计算95%置信度下VaR值为2.8015,99%置信度下VaR值为3.9682。可以看出通过建立GARCH(1,1)模型对数据拟合后计算出来的VaR值能够对投资者投资恒生电子这一单一金融资产起到参考作用,可作为其控制风险的一种手段。
三、总结与建议
经过以上研究我们可以得到如下结论:单一证券投资个股恒生电子的对数收益率不严格符合正态分布的特征,收益率时间序列有明显尖峰厚尾、波动性集聚的缺陷,与此同时,建立GARCH(1,1)模型可以很有效率的对此特征进行研究,并且这种方法适合我们国家的不够完善的金融市场;另外,通过将计算的VaR值与实际值进行比较可得知,用方差-协方差法计算的VaR值较大,相对应的风险很高,说明虽然VaR方法可以对我国的金融市场投资者提供一定参考思路,但是其也留有一定缺陷,模型有待进一步改进。
