两点爆炸荷载下地铁隧道动力响应数值分析
2020-08-18刘家绮
刘家绮,赵 敏
(西安工业大学 建筑工程学院,陕西 西安 710021)
1 引言
随着制导武器的发展,地下结构的抗爆性能越来越被重视。不同爆点产生的冲击波在爆点对称面处发生碰撞[1],聚能效应会加剧结构的破坏。因此,研究多点爆炸对于地铁隧道的毁伤评估具有重要价值。
许多学者就多点爆炸进行了大量研究。顾文彬等[2]研究发现水中两点同时爆炸,冲击波相互作用叠加提高了爆炸威力。张世豪等[3]通过研究多点爆炸能量聚集效应,发现多点爆炸应力波会在装药对称位置发生叠加,进而扩大了毁伤区域。胡宏伟等[4]研究了多点同步地面爆炸,结果冲击波超压和冲量得到显著增大。孙少峰[5]研究了单层球面网壳内两点异步爆炸冲击波的传播规律,发现两炸点起爆时间不同时,冲击波相遇的位置和所具有的能量均有所变化。在上述研究基础上,本文对两点对称装药同步爆炸进行模拟,研究两爆炸冲击波相互作用规律及隧道结构的动力响应,为隧道抗爆设计提供借鉴。
2 数值模型及材料参数
本文两起爆点位于地铁隧道上方且垂直于隧道纵向轴线等药量对称分布,考虑对称性以XOY 面作为对称面建立1/2 模型;模型对称面采用对称约束,四周及底面设置为无反射边界,采用cm-g-µs 单位制。
两点对称爆炸模型如图1 所示,计算模型尺寸为30 m×30 m×30 m。隧道截面为圆形,外径为3 m,衬砌厚0.3 m,埋深12 m。两点装药量均为450 kg,炸点间距d取2 m、4 m、6 m、8 m、10 m、12 m、14 m 工况,埋深h取1 m、3 m、5 m。有限元模型采用SOLID164 三维实体单元,空气、炸药、土体采用Euler 单元,隧道结构采用Lagrange单元,两种单元之间通过关键字*CONSTRAINED_LAGRANGE_IN_SOLID 实现流固耦合[6]。
模型中,炸药采用*MAT_HIGH_EXPLOSIVE_BURN 材料和JWL 状态方程描述[7]。空气选*MAT_NULL 材料模型和*EOS_LINEAR_POLYNOMIAL 状态方程定义。土体采用*MAT_SOIL_AND_FORM 材料模型[8]。地铁隧道为整体式[9],并采用*MAT_PLASTIC_KINEMATIC 随动强化模型描述,其中衬砌密度取2.65 g·cm-3,杨氏模量取39.1 GPa,泊松比取0.25,切线模量取4.0 GPa,屈服强度取0.1 GPa。
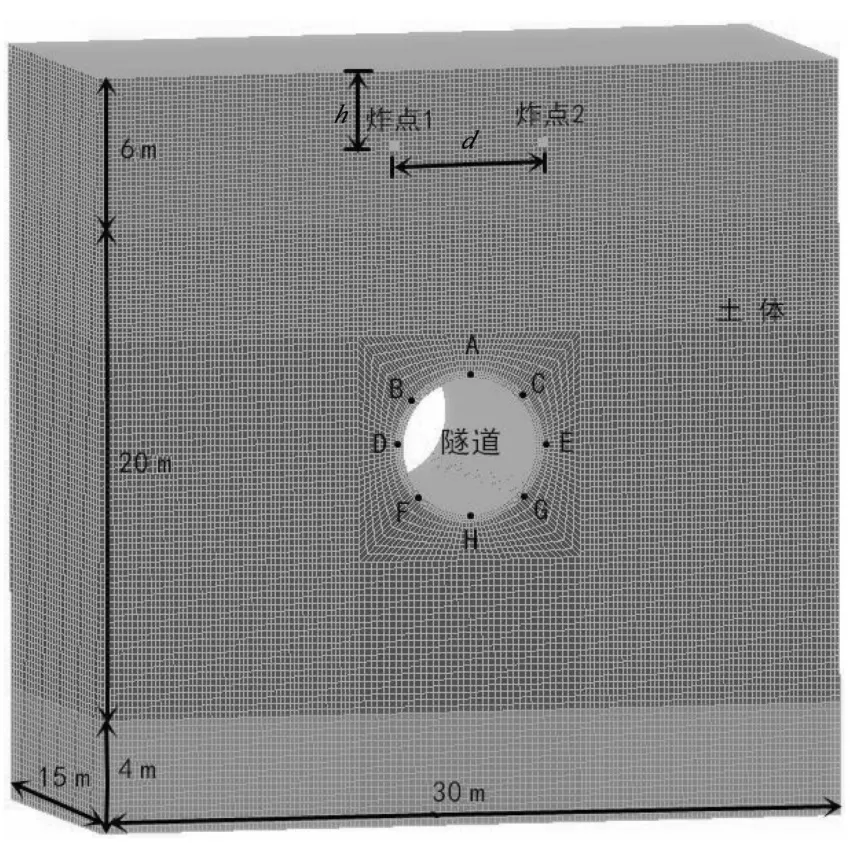
图1 两点对称爆炸模型
3 计算结果分析
3.1 两点对称爆炸冲击波的相互作用
两点对称同时起爆后,两冲击波碰撞前后的压力时程如图2 所示,碰撞前正向冲击波和反向冲击波的压力幅值分别为37.47 MPa 和37.36 MPa,两冲击波的波形和幅值基本一致,发生碰撞后,碰撞面处压力急剧增至84.31 MPa,大于碰撞发生前正、反向冲击波的压力幅值之和,并非是两个冲击波幅值的简单相加。
3.2 不同工况隧道响应分析
为了研究两点对称爆炸荷载作用下地铁隧道响应情况,选取炸点间距d为6 m、埋深h为3 m 工况隧道模型进行分析,不同时刻隧道von-Mises 应力云图如图3 所示。可以看出,在两对称爆炸荷载作用下,炸点所在面隧道截面应力最先受到影响。6 ms 时刻隧道上部正对装药对称中心区域应力先发生变化,同时隧道应力沿周向不断扩展;20 ms 时刻,隧道上部应力开始衰减,隧道下部应力开始产生明显变化;27 ms 时刻,隧道整体应力有所减小,拱底出现应力聚集。
在炸点连线所在隧道截面上,以隧道上部中心为起点,沿周向顺时针方向每隔45°取一个测点。各测点位置如图1所示。工况3 模型隧道周向位移随时间变化情况如图4 所示。可以看出,隧道上左右对称测点的水平位移竖向对称,其中点D、E 水平位移最大,达0.221 cm,而点A 和H 水平位移最小。各对称点的竖直位移基本一致,其中A 点竖直位移最大,达0.621 cm,H 点的竖直位移最小,A、H 两点的竖向位移差值先减小后增大。表明该时间段内由于隧道自身的弹性作用,其横截面先保持圆形,约在30 ms 时圆形截面开始发生不均匀变形和沉降。
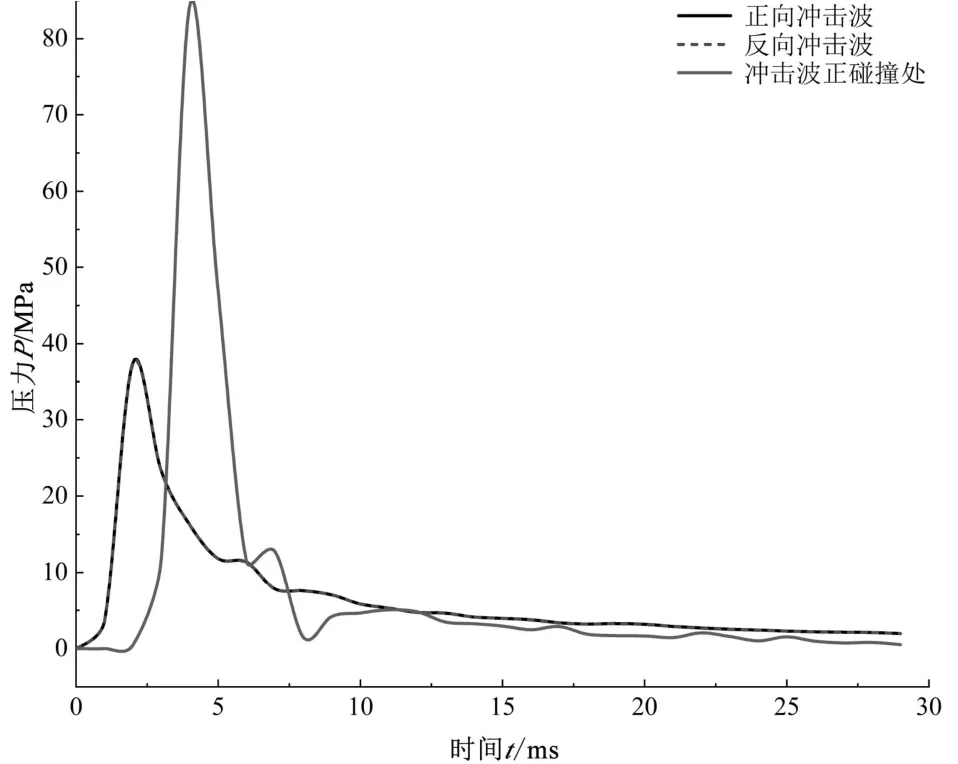
图2 冲击波正碰撞压力时程曲线
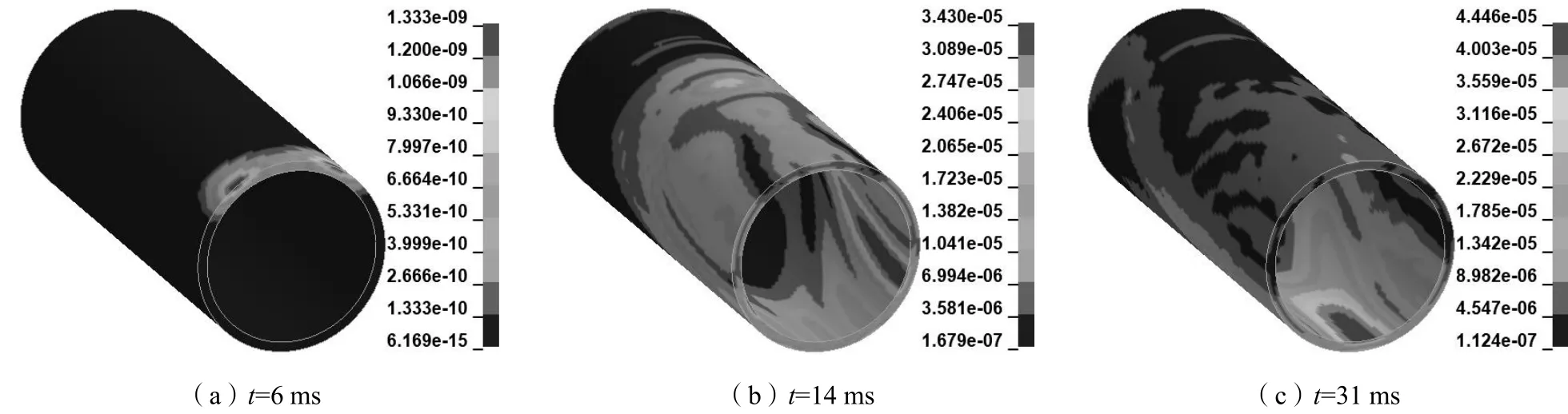
图3 隧道von-Mises 应力云图

图4 隧道截面沿x 和y 方向位移时程曲线
隧道周向各点应力曲线如图5 所示。爆炸初始,各位置应力发生小幅度波动;随着爆炸能量扩散范围的增大,土层对地铁隧道的挤压作用增强,同时在压缩波及拉伸波反复作用下,点1、2 及5 以受压为主,点3 和4 主要受拉,随着冲击波的衰减,土壤挤压作用减小,点1 和5 由受压状态转为受拉状态,而点3 由受拉转为受压。由于混凝土的破坏大多是拉伸破坏,可见隧道底部及拱腰等处易先出现拉裂 脱落。以隧道拱顶为起点,顺时针方向记为隧道0°~330°,相同埋深及当量条件下,不同炸点间距隧道各处最大等效应力如图6 所示,可以看出隧道截面上应力呈竖向对称分布,且最大应力随d的增加先增大后减小,d越大,底部“端部效应”越明显。d<10 m 时,最大应力位于72°~90°及270°~288°范围内;d≥10 m 时,最大应力位于 125°~130°及 230°~235°范围内。炸药当量和间距一定,不同埋深隧道各处最大等效应力如图7 所示。可知炸点埋深增加,隧道截面各处最大应力增大。
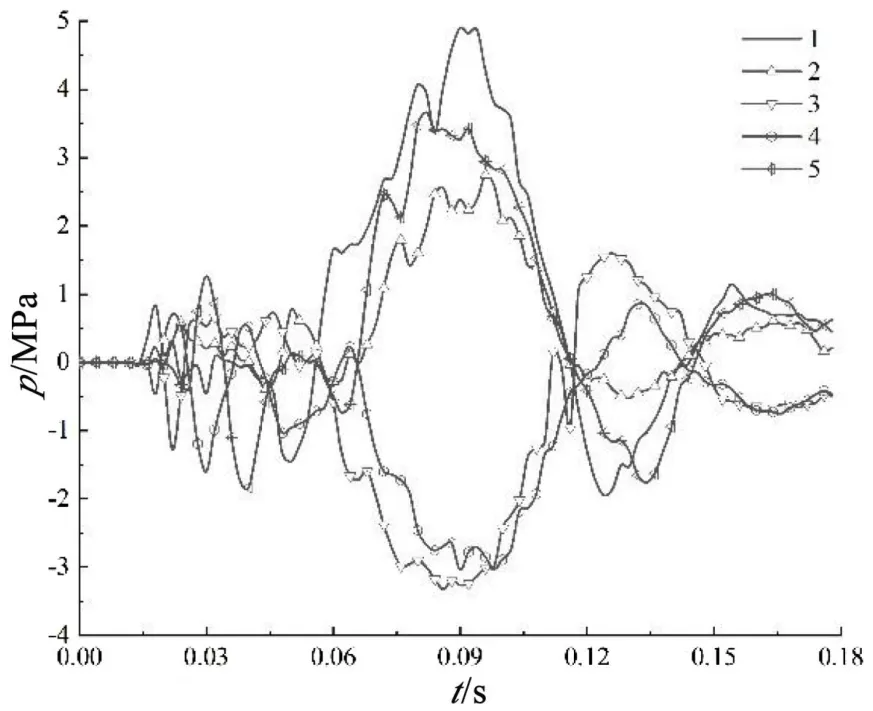
图5 隧道周向压力时程图
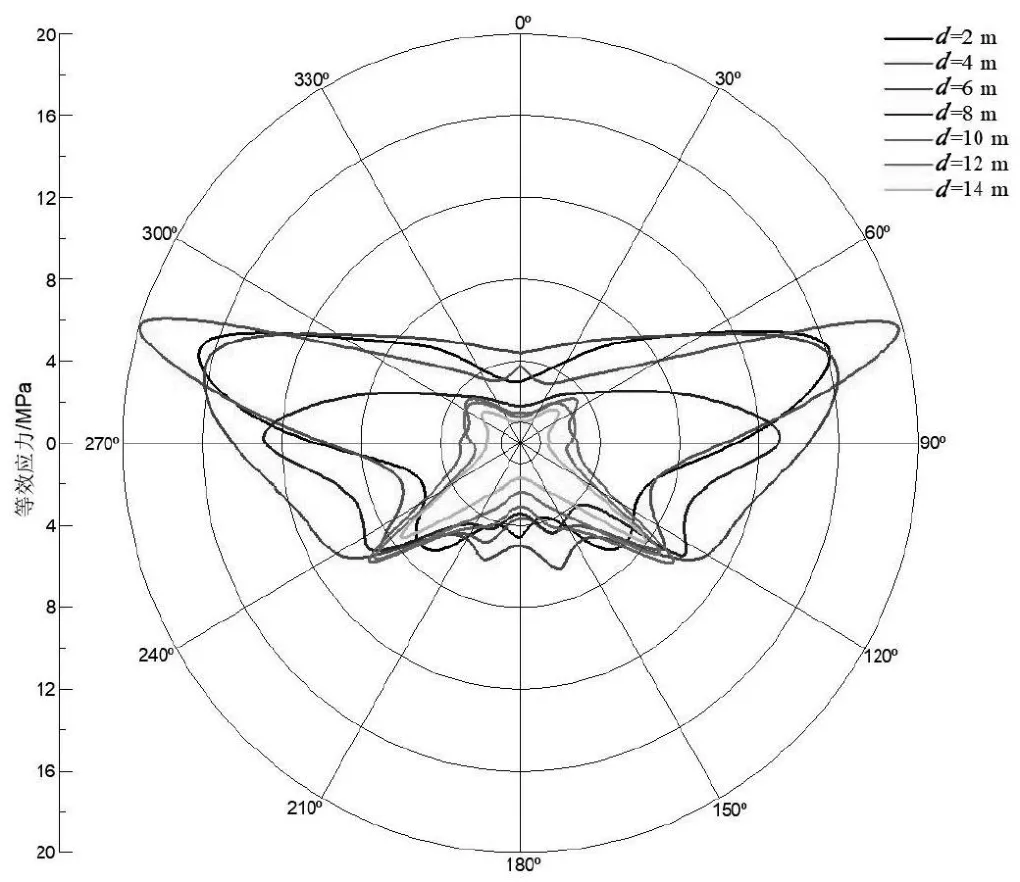
图6 不同炸点间距隧道截面最大等效应力
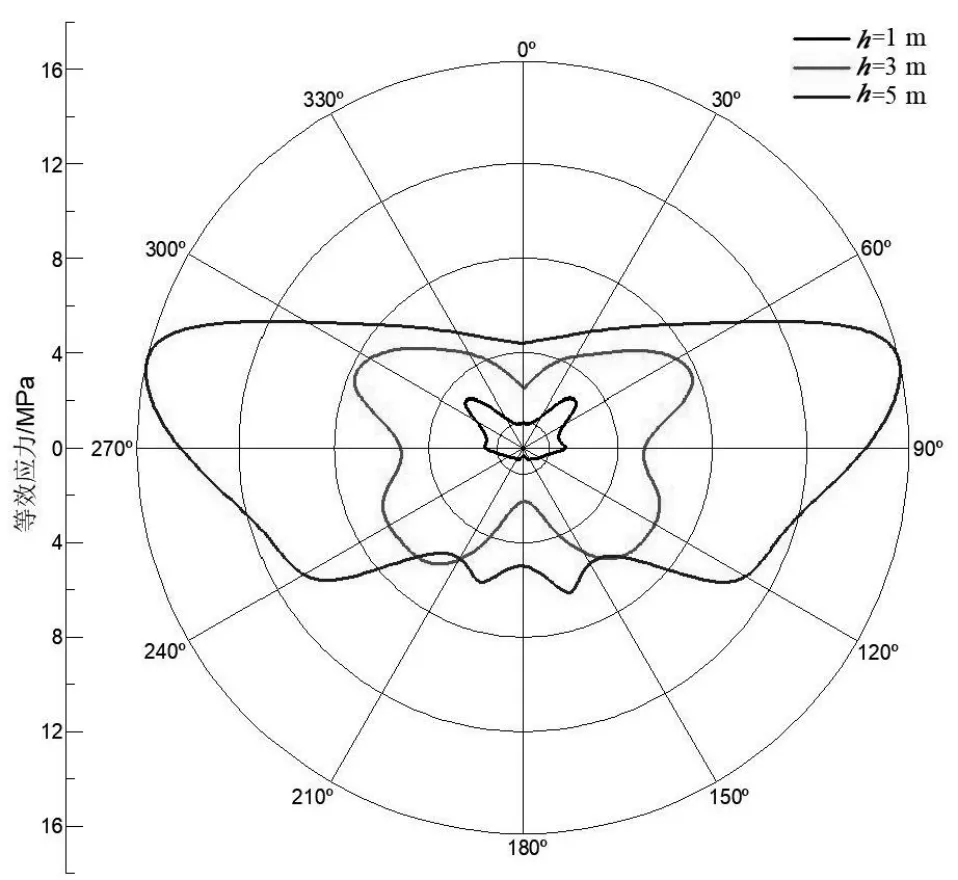
图7 不同炸点埋深隧道截面最大等效应力
4 结论
通过LS-DYNA 软件模拟了两点对称同时爆炸,对不同炸点间距及埋深下地铁隧道动力响应的结果进行对比分析,主要得到以下结论:①土中两点同时起爆时,两相向传播的冲击波在装药对称位置发生正碰撞,碰撞界面处压力急剧增加,碰撞面上强度大于两冲击波的强度之和,并非两个冲击波压力的简单线性相加。②在两对称爆炸荷载作用下,隧道衬砌拱顶、拱底及拱腰等位置易先发生损坏。爆点间距增加,荷载分布范围增加,结构的动力响应先减小后增大再减小;两爆点埋深越大,隧道动力响应也越大。
