高中数学概率教学试题探究———以2019年文科和理科全国卷为例

◇ 山东 李衍利

随着科技的不断发展，教育也得到了丰富和发展，同时也被赋予了不一样的内涵，各个学校开始注重建设新的课程体系，越来越多的高中注重和大学知识的衔接.数学是很多学科的基础，高中数学会涉及概率知识，可以认为高中数学的概率知识是大学数学概率和统计知识的基础.笔者认为概率知识可以培养学生的学习意识，提升学生的学习能动性，同时可以充分体现当代数学的有效性以及应用性.

1 注重概念教学，丰富课堂的教学内容

概率统计相关的知识与实际生活息息相关，能够让学生进行全方位的思考，教师在教学的过程中要鼓励学生积极参与到课堂教学中，培养学生自主学习的意识，提高学生的思维能力.概率教学并不仅仅是为了让学生不断学习、不断总结，进行题海战术，而是要让学生掌握统计思想以及统计的解题方式，并且让学生能够把课堂上学到的概率统计知识用于日常生活中，真正地学以致用.也就是说，教师要优化课堂的教学步骤，提升学生的理解能力，有效地分析教材上的题型，加强学生的记忆以及理解，培养学生的学习能力.另外教师还要把教材里抽象的概率概念具体化、形象化，提高学生对概率知识的理解程度，让学生能够运用自己的思维去思考.

例1(2019 年全国卷Ⅰ)我国古代典籍《周易》用“卦”描述万物的变化.每一“重卦”由从下到上排列的6 个爻组成，爻分为阳爻“——”和阴爻“— —”，图1就是一重卦.在所有重卦中随机取一重卦，则该重卦恰有3个阳爻的概率是( ).

图1

分析本题主要考查利用计数原理与排列组合计算古典概型问题，既渗透了传统文化又体现了数学运算这一核心素养.“重卦”中每一个爻有2种情况，该重卦恰有3个阳爻是相同元素的排列问题，利用直接法即可求解.

详解由题知，每一个爻有2种情况，一重卦的6个爻有26种情况，其中6爻中恰有3个阳爻情况有，所以该重卦恰有3 个阳爻的概率为故选A.

本题是利用排列组合知识计算古典概型，求解时首先要分析元素是否可重复，其次要分析是排列问题还是组合问题.

2 认真设计教学方案，提升课堂的教学效果

概率统计知识的教学内容以及研究的对象不确定性很强，容易让学生出现思维混乱以及解题错误的情况，所以教师在教学的过程中要把教材上传统的教学内容进行充分研究和分析，让学生学会灵活地思考和分析问题，以应对复杂多变的概率统计内容.对于概率的定义，教师要利用实际事例给学生分析，让学生掌握其中的规律.概率指的是可以进行重复性实验的状况下，随机事件发生的频率大小.在教学的过程中，学生如果没有认真研究，那么这个知识点并不容易被理解，所以教师要把教材上的概念转变成自己的语言，引导学生进行思考，并结合例题给学生进行详细的分析.

例2(2019年全国卷Ⅰ)甲、乙两队进行篮球决赛，采取七场四胜制(当某队赢得四场胜利时，该队获胜，决赛结束).根据前期比赛成绩，甲队的主客场安排依次为“主主客客主客主”.设甲队主场取胜的概率为0.6，客场取胜的概率为0.5，且各场比赛结果相互独立，则甲队以4∶1获胜的概率是.

分析本题应注意分情况讨论，即前5场甲队获胜的2种情况，需用独立事件概率的计算公式求解.题目有一定的难度，注重对基础知识、基本计算能力及分类讨论思想的考查.

详解前4场中有1场客场输，第5场赢时，甲队以4∶1获胜的概率是

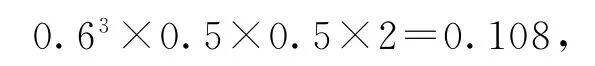
前4场中有1场主场输，第5场赢时，甲队以4∶1获胜的概率是

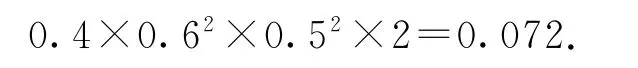
综上所述，甲队以4∶1获胜的概率是0.108＋0.072＝0.18.

本题题干较长，解题的关键点主要包括3个，其一是能否静心读题，正确理解题意；其二是思维的全面性，要考虑甲队以4∶1获胜的2种情况；其三是能否准确计算.

3 结合具体案例教学，提升解决问题的能力

概率知识对于学生来说有些难懂，部分知识点容易存在盲区，所以教师在教学的过程中要给学生正确讲解其中的定义，不要让学生出现思维上的偏差.在教学的过程中，教师要根据学生的具体情况设定合理的教学目标.教材中并没有对概率进行详细的描述，所以教师要根据概率统计的特点，结合自己的教学经验，激发学生学习的能动性，让学生了解概率的定义以及相应的公式，这样才能够给学生打好基础，提高学生解题的效率.在教学的过程中，教师不能盲目选择教学的素材，要有理有据，素材的选择不在多而在精，要能够帮助学生有效思考，提升学生的想象能力.

例如，有一个自来水公司为了能够让居民养成节约用水的好习惯，试运行了用水的定额管理办法，居民每个月用水的标准都没有超出一定的标准，就按平价收费，超出的部分就按议价收费.在保证居民日常生活的情况之下，应怎样来制定这个标准?

在这个问题中，教师可以让学生进行讨论.学生需要知道居民的用水情况，表现在数学里面就是要知道频率分布，进而就要知道怎样去画概率分布直方图，以及直方图的特点是什么.

经过讨论，学生认为要利用抽样调查这种方式收集样本数据，来对居民的用水量分布情况进行估计，根据这一情况来制定收费标准比较合理.通常学生会用直方图来反映频率的分布，绘制直方图的步骤包括求这组数据的极差，然后确定组数和组距，把数据分别列出，画出频率的分布表，最后画出直方图.频率分布直方图有自己的特征，在直方图上能够一目了然地得到数据的总体趋势，但是在直方图上看不到原始的数据.另外，设定数据的不同，单位不一样，得到的形状以及图象也会有所区别，这样会影响判断，所以要认真观察.

例3(2019年全国卷Ⅰ)某商场为提高服务质量，随机调查了50名男顾客和50名女顾客，每位顾客对该商场服务给出满意或不满意的评价，得到列联表，如表1.

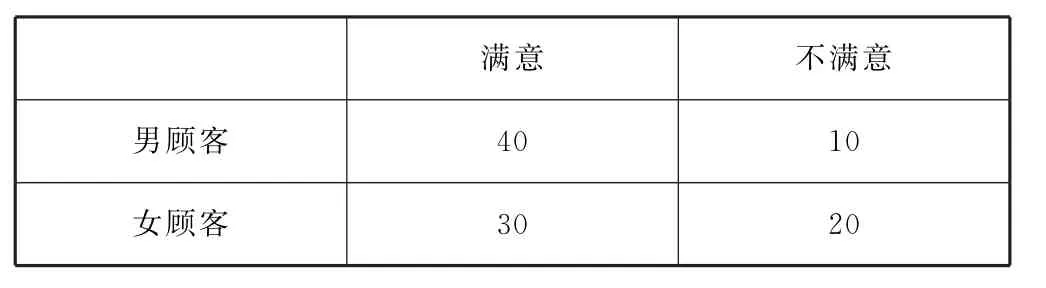
表1

(1)分别估计男、女顾客对该商场服务满意的概率；

(2)能否有95%的把握认为男、女顾客对该商场服务的评价有差异?

附

表2

分析本题主要考查独立性检验的基本思想，第(1)问比较简单，就是一个常规的概率问题.但是第(2)问涉及独立性检验，学生要确定两个分类变量之间的关系，按照所学的知识去一步一步推理，这个问题对学生来说不难.

详解(1)由调查数据可知，男顾客中对该商场服务满意的比率为因此男顾客对该商场服务满意的概率的估计值为0.8.

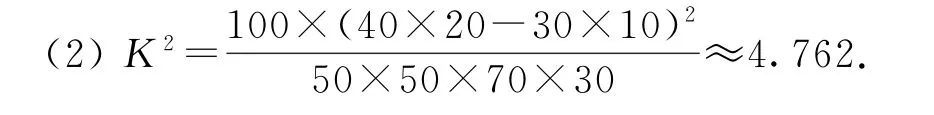
由于4.762＞3.841，故有95%的把握认为男、女顾客对该商场服务的评价有差异.

这道题题目内容比较少，题目中已经给出公式，我们只需要代入数据就可以算出K2，再结合给出的临界值表作出判断，这道题就很容易地解决了.

总而言之，在概率统计教学的过程中，教师要站在学生的角度思考问题，根据学生的具体情况去设置合理的教学目标，利用实际生活和生产中的案例引导学生理解相关概念，不断丰富课堂的内容，提升课堂教学的质量，激发学生的主观能动性，提高学生的数学核心素养.