自适应连续集稀疏分解声音识别算法

李丹鹤，陈晓东

（1.唐山工业职业技术学院，河北 唐山 063200；2.辽东学院工程技术学院，辽宁 丹东 118000）

1 引言

公共场所的安全防护和广场、街道等区域突发事件的实时监测，随着经济的发展越来越受到高度重视，异常事件的发生通常伴有尖叫、物品破碎及爆炸等与事件相关的异常声音，准确识别这些公共场所的异常声音以辅助安全监控对维护秩序、保护公共财务和公民安全，具有重要的研究意义[1]，已成为当前公共安全领域研究发展的重要方向。

国内外学者对各种环境下的异常声音事件检测展开了大量研究，文献[2]在对异常声信号进行经验模态总体平均分解基础上，提取分解固有模态函数的MPCC、短时能量等特征，提取方法，并采用改进无环图SVM 进行识别，但算法仅适于五种特征信号；文献[3]借助粒子群算法的连续字典集特性对粒子滤波进行优化改进，然后将改进的粒子滤波用于SVM 中，以提高SVM 跳出局部最优的能力，从而提高算法对公共环境中异常声音的识别率并降低算法复杂度；文献[4]提取异常声音信号的过零率、相关系数、MPCC 等多特征组成复合特征，通过粒子群优化改进的SVM 算法对四类声信号进行分类。文献[5]通过判决表示和声谱图提取异常声音信号的组合特征并将SVM 和神经网络的分类识别优势融合后对组合特征进行分类，但算法在多隐层DNN 训练时易形成深层错误问题。

由于公共场所的背景噪声具有非线性和存在耒知突变等复杂性，已有方法进行实际环境的异常声音识别时往往噪声干扰过强而达不到理想识别效果[3]。正交匹配追踪（Orthogonal Matching Pursuit，OMP）[6]遵循信息的自适应分解原则，通过在一个过完备集中追踪时频特征能够自适应最佳匹配原始信号内部结构的最优原子，实现声信号的稀疏分解并重构，适于非平稳非线性噪声环境下的声音事件识别。文献[6]通过冲激响应稀疏模型优化MP算法提取声信号的时频参数特征，但参数难以保证对非平衡背景噪声的适应性；文献[7]通过反卷积法优化MP 重构声源信号，基于数值仿真成像图和偏差值分析声源信号的频率、信噪比等特征；文献[8]采用基于优化OMP 和短时谱估计的二次重构方法消除公共环境中的非平衡非线性噪声，然后提取MPCC 和MP 时频参数等特征通过DBN 实现声信号识别，并通过40 种声事件对算法的有效性进行了验证。

在已有研究基础上，提出基于自适应连续集MP 稀疏分解的公共环境异常声音识别算法。算法通过相关参数的自适应改进实现自适应PSO 算法，然后借助PSO 算法的连续空间搜索优势对MP 稀疏分解进行优化和构建连续Gabor 超完备原子集，从而提高稀疏分解获得的最优原子的匹配度，最后提取重构声信号的复合特征以SVM 算法实现异常声音事件的快速准确识别，实验验证了算法的有效性和对公共环境噪声的鲁棒性。

2 OMP 信号稀疏分解

匹配追踪的思想是将信号表示为一系列最优匹配的时频原子的线性组合，利用最优原子精确描述含噪信号中的纯净目标信号。数学上，OMP 通过Hilbert 空间H=RN的一个过完备集D=｛gi，i=1，2，L，Q｝中的原子组 a=｛a1，a2，L，am｝来线性组合表示信号f∈H，即 f=a·g，如果 a 中大部分值近似于 0，则认为 f=a·g 是稀疏的。

遍历过完备集中的所有原子，利用式（1）所示内积计算式搜索最优原子，即时频原子可以最优的逐步匹配原始信号的某一特征，

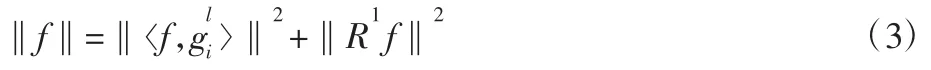
为使‖R1f‖取得最小值，以使最优原子组线性组合最优表达原始信号，须在每次迭代时取得最大值。令MP 迭代开始时f=R0f，进行k 次迭代后的剩余信号为fk=Rkf，则以其作为待匹配信号，继续重复式（1），在D 中搜索最优匹配原子D，则得到分解所得的最优原子，即满足：

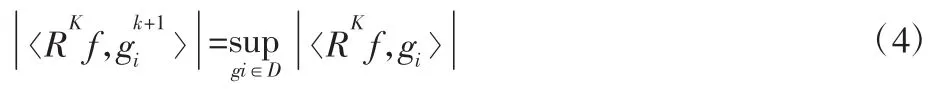
不断重复式（1）直到剩余信号振幅小于预设并值，此时，原始信号f 的MP 稀疏分解可表示为：

OMP 算法在稀疏分解的每次迭代过程中，都需要遍历D 中的所有原子以搜索剩余信号的最优匹配原子，因而计算量巨大，且要求D 为有限[5]，通常选择参数离散方式获得的Gabor 集作为过完备原子集。这样，在进行实际声音检测时，MP 稀疏分解对γ 的离散化和Gabor 集的冗余性需求，本质上存在一定的矛盾。PSO 算法能够实现连续空间的全局搜索优化[6]，因而通过目标函数调整改进，可以将PSO 的连续空间能力用以改进MP 稀疏分解，提高最优匹配原子的匹配性能。

3 PSO 优化MP 声信号识别

3.1 自适应学习PSO 算法

PSO 算法[10]将种群的个体视为多维空间搜索的粒子，以位置、速度和适应度三个特征值表示第个粒子特征，m 个粒子在d维空间以一定的速度飞行，根据自身与其他粒子的飞行经验，即个体历史最优和种群历史最优，改变其飞行的速度和方向，从而实现全局搜索的寻优过程。种群惯性权重用以平衡全局探测和局部开采，学习因子控制粒子向最位置飞行的步长。

借助密度聚类方法，将种群粒子自适应划分，子群采用不同的学习策略以提高多样性。对每个粒子赋于局部密度ρi和间距两个变量，定义为：

式中：dii—两粒子之间的距离；dc—其截距，当某子类的局部密度最大，则有ρi=maxidij。根据式（6）可得子群的聚类中心为ρi和δi都较大的粒子，其他粒子则可以归入与其距离最近的中心粒子局部子群中。

划分后对子群内的非最优粒子需要基于最优粒子位置引导，提高其局部搜索能力以获得更优位置，采用式（7）进行位置更新，即：

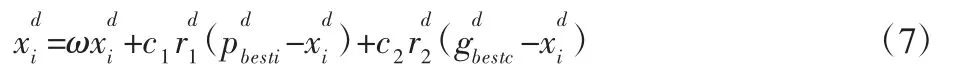
式中：ω、c1和 c2—PSO 算法的惯性权重和学习因子—位于［0，1］且满足均匀分布的随机数—子群c 的最优位置粒子，而对于需要根据种群历史最优进行位置和速度的更新，更新公式为：

每个子群中的最优粒子是全局最优解的可能性最大，因而采用式（8）子群平均信息引入其更新，以加强子群寻优信息交互，避免局部最优。

已有研究表明，增加扰动到粒子更新过程中有利于帮助粒子跳出局部解，因此采用高斯变异进一步增加PSO 粒子多样性，避免局部最优。由高斯概率函数重构高斯变异函数Gi（t）：

经过一定迭代次数后，大部分粒子位置向最优粒子飞行，易造成算法“早熟“，为此，采用Gi（t）增加扰动，以减少粒子进入局部解的概率，基于高斯变异扰动的粒子位置更新式为：

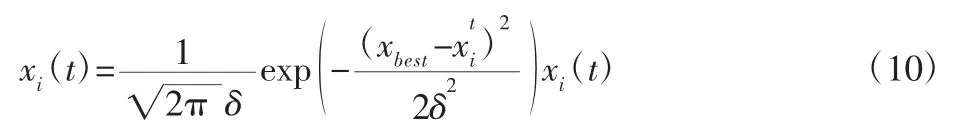
3.2 改进算法的目标函数构建

基于高斯窗函数伸缩变换得到的Gabor 字典集，其信号特性与声事件特性相关性较好[10]，基于PSO 函数的连续空间搜索能力，采用连续Gabor 过完备集进行改进MP 稀疏分解。

设含噪声信号为f=fs+fn，式中：fs—纯净声信号，而fn—噪声。则文中PSO 改进MP 的目标函数为：

根据目标函数，初始化后，在迭代过程中，根据适应度函数更新粒子的位置和速度。迭代次数的增加会使最优字典集的维数逐渐增高，使算法在重构信号时复杂度激增，为此采用Hermitian求逆实现信号重构。

分块形式表示Hermitian：

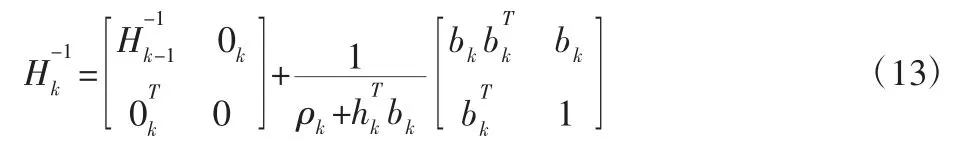
根据式（13），在信号重构时，当次矩阵求逆可以表示为前次求逆结果线性组合，从而提高矩阵求逆效率。

设PSO 改进MP 稀疏分解的每次迭代更新后，原子集字典变为 DΔk=［DΔk-1gyk］，gyk—当次迭代更新后获得的最优匹配原子，则有：ΘΔk=［ΘΔk-1dyk］，其中，ΘΔk=φψΔk，dyk=φgyk。φ 为观测矩阵。

熟悉金刚石专业加工设备的操作及维护，金刚石刀具结构设计，金刚石模具装配、装料和取料，掌握金刚石检测工具的选择与合理使用及加工工艺。

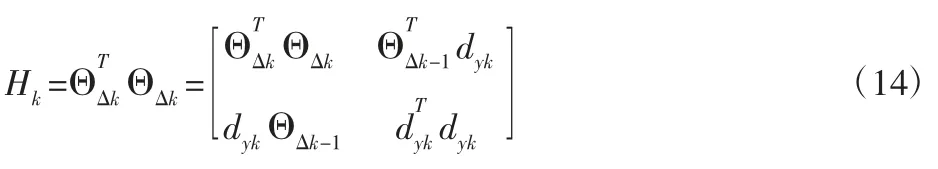
图1 改进算法的稀疏分解流程Fig.1 Improved Algorithm Sparse Decomposition Process

3.3 异常声音事件识别

通过高斯函数变换获得的Gabor 集中的原子能够较好的描述公共环境中异常声信号的时频特性[9]，而与环境背景噪声的相关性较低，因而实际环境中获得的含噪信号经改进MP 稀疏分解算法分解后，其最优原子组的时频参数集合可以较好的描述实际信号中的纯净声信号，而有效消除噪声干扰，可以作为声信号识别的特征，这里以时频参数集合中的与的均值和标准差作为公共环境异常声音的识别特征。设实际采集声信号经预处理后被分为M帧，则采用改进算法对信号完成MP 稀疏分解后，最优原子组中的s与 v 分别为 s=［S1，S2，L，Sλ，L，SM］和 v=［v1，v2，L，vλ，L，vM］，识别特征为 Fmp（λ）=｛u（Sλ，vλ），σ（Sλ，vλ）｝。

SVM 可以在训练样本量较少的情况下取得最优的分类识别结果，适合公共场所的异常声识别环境。为此，采用SVM 算法以提取的 Fmp（λ）=｛u（Sλ，vλ），σ（Sλ，vλ）｝进行声信号识别。

4 实验分析

为验证改进算法（简记为APso-MP）在公共环境噪声下的异常声音识别性能，实验以DCASE[10]库中的5 种室内声音和10 种公共场所异常声音为数据，选取雨天环境噪声、车站环境噪声、闹市环境噪声和高斯噪声四种噪声进行不同信噪比混合，以仿真实际环境实测声信号，采样率fs=22.05Hz，训练样本100 组，测试样本30 组。最大迭代次数kmax=200，粒子群算法的位置边界Xmax=［N，N，π，2π］，初始位置为边界内随机值。

4.1 改进算法信号重构性能分析

从实验数据中随机50 组声信号样本，并与四种噪声以－5 dB 分段信噪随机混合，改进算法对某含胡高斯噪声的声信号稀疏分解并重构后的波形图和时频谱图，如图2 所示。可以看出，算法较好的降低噪声干扰，并保持声信号波形，时频谱图中也显示出算法较好的降噪作用。进一步，采用这里算法、PSO 改进MP 算法（记为 Pso-MP）[4]及原始 OMP 算法对重构信号的均方误差（MSE）、波形相似性（NCC）[9]及信噪比（SNR）等评价指标进行分析，多次实验结果平均值，如表2 所示。

图2 改进算法重构信号Fig.2 Reconstruction Signal of the Proposed Algorithm

表2 实验结果进一步验证了这里改进算法在信号稀疏分解和重构方面的优势，自适应的参数设置增加算法对不同异常声信号的适应性，而连续集最优原子增加了与声信号的匹配程序。

表2 重构性能分析实验结果Tab.2 Calculation and Reconstruction Performance

4.2 异常声信号识别性能实验

为验证算法别性能，以识别率p=（U1/U）×100%为指标，式中：U—总样本数；U1—准确识别样本数。将这里APso-MPSVM 算法与 OMPSVM[10]、Pso-MPSVM[9]、APso-MPRF 三种已有算法进行声信号识别性能比较，APso-MPRF 算法为以文中改进MP 稀疏分解重构信号而采用树数500 分类属性5 的随机森林作为分类器。将测试样本以不同分段信噪比与噪声混合进行识别，多次实验平均值，如图3 所示。

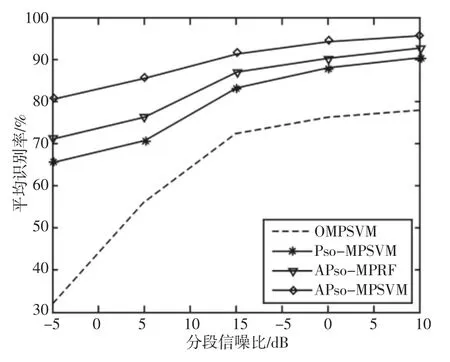
图3 实验算法在4 种噪声环境的声音识别率Fig.3 Average Recognition Rate of Each Algorithm in 4 Noise Environments

从图3 中可以看出，APso-MPSVM 算法的异常声信号识别率最高。在分类器相同下APso-MPSVM 算法比APso-MPSVM 算法的平均识别率更高，说明APso-MP 分解获得的最优原子组参数具有更好的识别性能，主要因为参数自适应设置使得算法对不同声信号具有更好的适应性，而连续超完备集的使用又使最优原子与声信号匹配性更好。

5 结束语

为实现公共环境复杂背景中异常声信号识别以辅助公共场所安全监控，提出基于连续完备集的自适应MP 稀疏分解声音识别算法，算法通过相关参数改进实现自适应PSO 算法，然后借助PSO 算法的连续空间搜索优势对MP 稀疏分解进行连续集优化，从而提高稀疏分解最优原子的匹配度，最后提取重构声信号的时频参数特征以SVM 算法实现异常声音事件的快速准确识别。实验结果表明，与已有算法相比，所提识别算法显著降低了计算量，并取得了最优的声音识别率和识别鲁棒性。