一种距离特征融合的机械三维模型检索方法

杨 岩，张 红，何 苗，路世青

（重庆理工大学机械工程学院，重庆 400054）

1 引言

随着三维CAD 技术及数字化设计技术的发展，三维模型已经在机械设计、动画设计及分子生物学等领域得到了广泛的应用。统计分析表明，在现代工业产品的设计中，约40%是重用过去的设计，约40%是对已有设计的微小修改，只有约20%是完全新的设计[1]。所以，在新产品研制过程中，快速准确地找到与设计需求相似的已有模型并加以重用，是提高机械设计效率、缩短产品开发周期的关键之一。针对三维模型检索，文献[2]提出了D2 形状算子，其通过计算任意点对间的欧式距离，并构建形状直方图来描述模型的特征，以此进行模型匹配。文献[3]采用模型表面顶点关联的三角形面积构造了面积序列，然后对其进行归一化操作和傅里叶变换等处理，最终得到面积分布算子，取得了较好的检索效果。文献[4]提出了一种基于曲度特征的三维模型检索算法，可同时克服平均曲率对平滑模型的不敏感性和高斯曲率分布较均匀的缺点，能够更真实地反映三维模型的局部弯曲程度，非常适用于曲面模型的特征描述，但不能直接用于机械零件的检索。文献[5]采用准随机数发生器产生随机数，计算任意两点有向线段距离及所在面面积之间的比值，同时以距离、面积比为坐标轴构建网格坐标系，统计出现在相应网格中特征点的频次，形成距离-面积特征分布矩阵，算法在应用于农机CAD 模型时，得到了较好的检索性能。文献[6]提出一种局部匹配方法，首先选取零件已有的典型结构，然后通过典型结构的面之间的拓扑关系进行检索。

提出一种结合D2 距离与协方差距离的三维模型检索方法，对三维模型的特征描述更充分。不仅能有效提高检索效率，同时对噪声、采样密度的变化也具有较好的鲁棒性，在对机械三维模型检索时取得较好的效果。

2 算法原理

协方差描述子[7]可以看作是一种对点的领域信息的抽象表示，它将代表不同特征的信息融合作为联合分布的采样，弱化了领域点的空间分布信息，且具有旋转、平移和缩放不变的特征，相比直方图描述子更具鲁棒性。

首先采用蒙特卡洛算法在三维模型表面随机取点，计算随机点对的D2 距离和协方差距离。然后对D2 距离和协方差距离进行联合统计，形成距离分布矩阵，以此矩阵作为模型的特征描述符。算法的实现步骤如下：（1）随机取点：在模型表面生成随机采样点。（2）计算特征距离：首先计算所有随机点的D2 距离，然后计算随机点对间的协方差矩阵，并得到协方差距离。（3）构建距离分布矩阵：以随机点对D2 距离为x 轴，协方差距离为y 轴构建一平面网格，统计网格中距离出现的频次，从而得到一个m×n 的特征矩阵。（4）模型相似性评价：采用曼哈顿距离评估模型之间的相似性。

3 算法实现

3.1 模型表面随机取点

采用文献[2]提出的蒙特卡洛方法进行随机取点，以模型表面三角形面片的面积大小为依据。首先，定义一个三角形面片Ti，利用海伦公式计算三角形面片的面积Si。

式中：qi（qi=（ai+bi+ci）/2）—三角形周长的一半。将所有三角形面片面积相加得到模型表面积S，则随机选取三角面片Ti的概率可表示为：

把［0，1］区间等分成k 段，其中，第i 段的长度与P（Ti）在数字上是相等的，第j 个节点数值为前（j-1）个三角形面片的和，只要在［0，1］之间生成一个随机数，即能找到三角形面片的索引号i，如图1 所示。

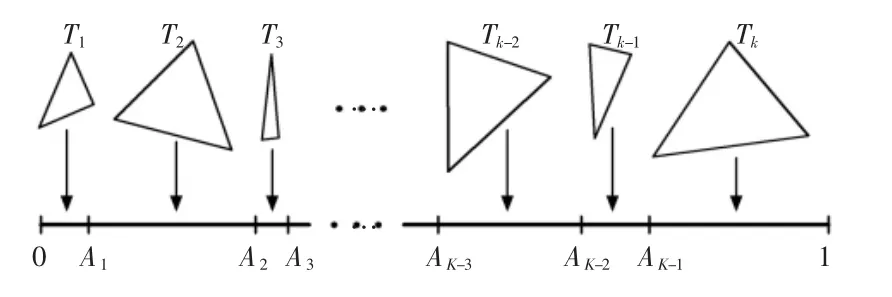
图1 三角形选取示意图Fig.1 The Diagram of Triangle Selection

随机点的位置将从上述选取的三角形中生成，方法是随机生成2 个介于［0，1］区间的数字 r1和 r2，随机点 p 的位置可表示为：

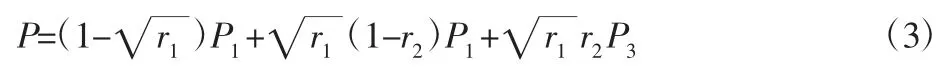
3.2 协方差距离及D2 距离计算

采用基于模型三角网格信息来提取特征，所以忽略模型颜色属性、材料属性等特征。根据文献[7]，协方差描述子可定义为随机变量从点云中提取出的一些列几何特征。文中只考虑三个角度特征，这样可以大大减小计算量，且具有平移、缩放和旋转不变性。建立协方差描述子的第一步是建立特征向量φ。

φ=（P1，P2，…，Pm-1，Pm）表示三角形 ABC 邻接三角形的中心点集合，α 是随机点 P 法向量 n 和的夹角，它表示以P 点为中心的局部凹凸状况，如图2 所示。β 表示Pi点的法向量和的夹角，它可衡量P 点领域内的局部曲率。γ 是P 点的法向量和Pi点法向量的夹角，作为一个3D 的空间角，它以一种非模糊的方式表示了局部曲面信息。随机点所在位置的局部特征将用这三个角度进行表征。

图2 协方差矩阵计算Fig.2 Calculation of Covariance Matrix

它们分别可用如下公式进行计算：

因此，随机点P 的协方差描述矩阵可表示为：

式中：up—三角形ABC 所有邻接三角形特征向量φ 的平均值；m—ABC 邻接三角形的个数。C（P）—一个3×3 的正定矩阵，它的对角线元素表示的是每个特征分布的变化，而非对角线上的元素表示两两特征的相互关联特性。这样，每个随机点处的局部特征都由一个协方差矩阵来表示，而两个随机点的协方差矩阵之间的距离即为两点的协方差距离，它可表示两点局部特征的相似性。文中采用曼哈顿距离来计算矩阵的距离。D2 距离采用文献[2]中方法进行计算，该方法较为简单，故此处不再赘述。设模型的任意两个随机点 pA=（xA，yA，zA），pB=（xB，yB，zB） 对应的协方差矩阵分别为mA和mB，则D2 距离d 和协方差距离D 可表示为：

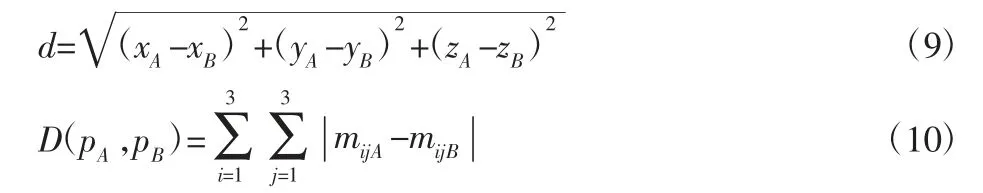
3.3 距离分布矩阵计算

以D2 距离为x 轴，协方差距离为y 轴统计两种距离特征的概率分布，以形成距离分布矩阵。具体步骤如下：

（1）将D2 距离和协方差距离区间分别划分为n1和n2等分，节点处的值分别为 di、Di。

（2）当 D2 距离和协方差距离同时满足 dk≤di≤dk+1，Dm≤Di≤Dm+1时，网格平面所对应的小方格加1，由此可以统计出D2 距离和协方差距离的概率分布。

（3）利用一个n1×n2的矩阵M 来表示上述网格，从而将三维模型特征用距离分布矩阵M 来表示。

3.4 模型的相似性度量

欧式距离和Manhattan 距离是两种常用的相似性度量方法，都具有计算简单、易实现的优点，但欧式距离在计算中没有充分考虑到各个分量之间的相关性，区分能力不足。所以文中采用Manhattan 距离来评价两个模型之间的差异性。Manhattan 距离是两个特征向量对应分量差值的绝对值求和。设三维模型A 与B的距离分布矩阵分别为MA和MB，则模型A 和模型B 的相似性度量函数为：

3.5 检索性能的评价

采用查全率-准确率曲线来评价算法检索性能，具体描述为：设查询模型为q，模型库Q 中与q 相似的模型数量为S，在Q中检索q 得到的检索结果集合为M，M 中与q 相似的三维模型数量为N，则查全率、准确率计算如下：

对于一个给定的查询模型，其查准率与返回的模型数量成反比关系，查全率与返回的模型数量成正比关系，查准率会随着查全率的增大而减小。所以查准率-查全率曲线是一条逐渐下降的曲线。在理想的情况下，查准率-查全率曲线应该为一条值为1的水平线。

4 实例检索与结果分析

为验证算法的有效性，采用普渡大学工程标准模型库ESB（Engineering Shape Benchmark）中的部分零件和来自微耕机传动机构中的部分零件作为检索对象，共计160 个三维模型，模型格式为OFF。实验平台为：IntelCorei3-3220CPU@3.3GHz。文中以代表性较强的齿轮类、轴类、端盖类零件作为实例检索对象，设置随机点个数为500 个，然后分别采用D2 距离算法[2]、直方图算法[8]、距离夹角形状分布算法[9]、算法进行实验，并按模型相似性从大到小顺序返回前9 个模型。实例检索结果，如图3 所示。查准率-查全率曲线，如图4 所示。不同算法平均时间，如表1 所示。

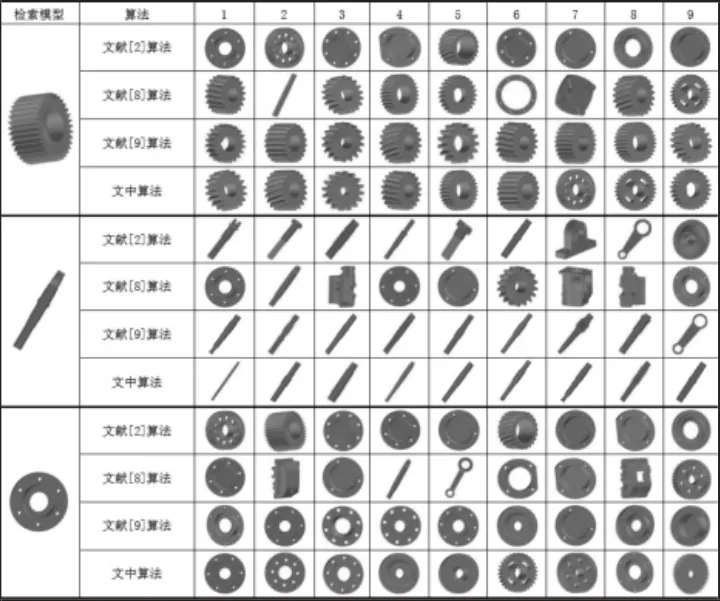
图3 不同检索算法的结果Fig.3 The Results of Different Retrieval Methods

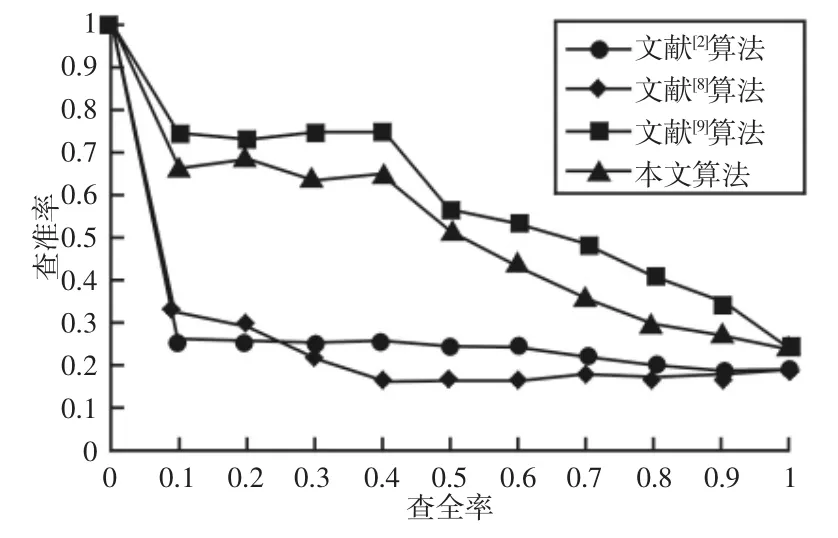
图4 查准率-查全率曲线图Fig.4 Precision-Recall Graph

表1 不同算法平均时间（ms）Tab.1 Mean Time of Different Methods（ms）

从检索结果不难看出，算法性能明显优于文献[2、8]中算法，特别是检索轴类零件时，文献[8]算法检索结果中仅仅只有一个是正确的。从形状上看，齿轮零件与轴类零件相差很大，但由于其空间点云分布相近，所以会被判定为同一类。这也显露出单一特征对模型形状描述不足的缺点。文献[9]和文中算法都采用了特征融合的方法，效果明显好于文献[2、8]。对于文献[9]中算法，虽然在检索效果上略优于文中算法，但相差并不大，另外，从算法平均时间上看，文中算法较文献[9]算法快了接近0.1s，0.1s 虽然对于只有160个模型的小型数据库来说很少，但当应用于大型模型库检索时，则可大大减少算法时间。所以，综合考虑查准率-查全率曲线和算法平均时间，文中算法较其它三种算法具有更好的检索性能。从全局特征和局部特征的思路出发，综合考虑D2 距离特征和协方差距离特征，避免了单一特征对模型特征描述不全的问题，提高了三维模型检索效率。

（1）采用的协方差距离特征同时考虑了随机点处的局部凹凸状况和局部曲率状况，对模型局部特征具有更好的描述能力，另外，协方差矩阵只受局部向量夹角的影响，而与模型的姿态无关，所以它还具有平移、旋转和缩放不变性。（2）D2 距离算法仅通过随机点间的距离来表征模型，无法全面的描述模型特征。这里在D2 距离算法的基础上引入了协方差距离描述符，可同时从全局特征和局部特征两方面对三维模型进行描述，避免了单一特征对模型特征描述不全面的问题，从而提高检索效率。实验表明，这里算法在时间和性能都能较好的满足检索需求，可适用于机械零件三维模型的在线实时检索。综上所述，这里算法一定程度上提高了机械三维模型检索的综合性能，对三维模型在线实时检索具有一定的参考意义。