复杂曲面五轴加工全局干涉检测

孙胜博，杜 娟，陈 峙，智红英

（太原科技大学机械工程学院，山西 太原 030024）

1 引言

随着以互联网为核心的第四次工业革命的蓬勃发展，人们对工业产品的性能和外观提出了越来越高的要求。由于五轴联动数控机床能够加工复杂曲面零件，特别是在加工航空发动机的涡轮叶片、汽车变速箱壳体、船用螺旋桨叶片和手机外壳等方面拥有巨大的优势，因此使用五轴数控机床进行复杂曲面加工得到了广泛应用。五轴数控加工相对于三轴数控加工拥有更好的灵活性，但是由于被加工复杂曲面凹凸变化不规律在曲率变化较大的区域，在加工过程中很容易出现全局干涉。全局干涉具有巨大的危害性，它可能导致刀具、夹具甚至机床床身的损坏[1-6]，所以对于五轴数控加工进行全局干涉检测及刀位修正研究是非常必要的。

文献[7-8]提出基于层次包围盒（OBB）的碰撞检测算法，将刀具用包围盒进行包裹，工件表面近似为一个八叉树基于三维投影的分离轴理论进行干涉检测，该算法较为繁琐计算量大且选取包围盒时需要在简便性和精确性之间进行取舍增加了选择难度。文献[9]提出基于自适应模拟退火遗传算法进行全局干涉检测，寻找自由曲面离散点到刀轴线段的最短距离并判断是否干涉，同时对干涉点进行相应的刀位修正。

针对环形铣刀五轴数控加工复杂曲面的全局干涉检测问题，首先将被加工参数曲面沿参数方向进行网格划分得到若干离散网格点，然后用六个平面包围环形铣刀的圆柱面形成包围盒，通过平面上指定点与加工曲面离散网格点连线的量与平面法向量的数量积的正负判断加工曲面离散网格点是否落在刀具包围盒内。若存在离散点落入刀具包围盒则进行精确检测并确定其是否在环形铣刀的圆柱体内，如果离散网格点落入环形铣刀的圆柱体内则存在全局干涉，否则不存在全局干涉；若没有离散网格点落入包围盒内则不存在全局干涉，则进行下一个刀位点的检测。

2 五轴数控加工模型及坐标变换

2.1 五轴数控加工复杂曲面建模

基于环形铣刀五轴数控加工复杂曲面的模型，如图1 所示。Σ为被加工的复杂曲面且Σ：r=r（u，v），分别以X、Y、Z 为坐标轴建立工件坐标系O-XYZ，CC 点为环形铣刀与加工曲面Σ的切触点。采用等参数法进行五轴加工且环形铣刀的刀具轨迹沿参数u方向，其中f 为切触点处沿参数u 方向的单位切向量，n 为切触点CC 处参数曲面Σ的单位法向量，根据右手法则得到v=n×f，以切触点 CC 为坐标原点，以向量 f，v 和 n 所在方向分别为 x，y 和z 轴，建立加工工件的局部坐标系CC-xyz。在图1 中，取环形铣刀底圆的中心点CL 作为环形铣刀的刀位点，并以刀位点CL 为坐标原点建立刀具坐标系CL-xtytzt。其中zt轴沿环形铣刀的刀轴方向，xt轴的初始方向与x 轴平行，yt轴用右手定则确定。环形铣刀的位置由刀位点CL 及刀轴的方向向量与工件局部坐标系中和坐标轴相关的两个夹角来确定，如图1 所示。环形铣刀首先以刀位点CL 为支点绕y 轴旋转得到前倾角λ（0≤λ≤π/2），然后再以切触点CC 为支点绕z 轴旋转形成摆转角ω（-π/2≤ω≤π/2）。五轴加工中当已知环形铣刀的刀位点、前倾角和摆转角后刀具的位置就可以确定下来。

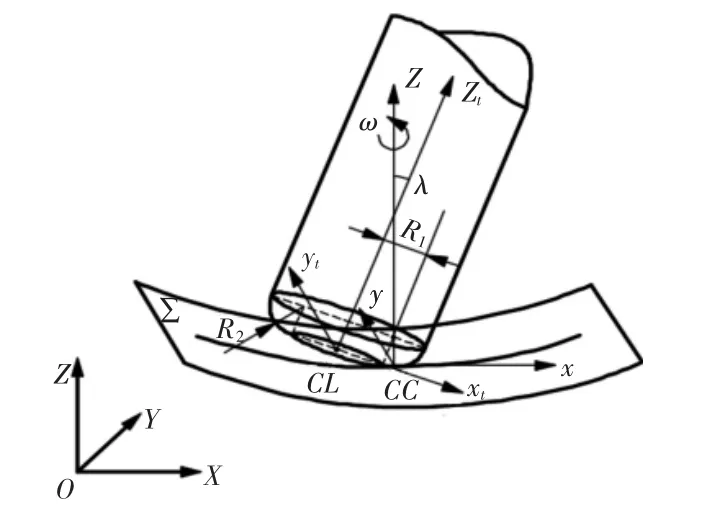
图1 环形铣刀五轴加工曲面模型Fig.1 Surface Model of Five Axis Machined Ring Milling Cutter

2.2 刀具坐标系与工件坐标系的坐标变换

根据图1 的环形铣刀与加工曲面Σ的相对位置关系可知，由刀具坐标系CL-xtytzt到工件坐标系O-XYZ 的转换过程需要两步，首先将刀具坐标系CL-xtytzt转换到加工工件局部坐标系CC-xyz，然后再将加工工件局部坐标系CC-xyz 转换为工件坐标系O-XYZ。刀具绕z 轴旋转ω 角后其转换矩阵Rz的表达式为：

刀具绕y 轴旋转λ 角后其转换矩阵Ry的表达式为：

将刀具坐标系CL-xtytzt中的原点CL 平移到与加工工件局部坐标系CC-xyz 中的原点CC 重合，其中，转换矩阵T 的表达式为：

因此，环形铣刀的刀具坐标系CL-xtytzt中的任意点在加工工件局部坐标系CC-xyz 下的坐标表示为：

加工工件局部坐标系CC-xyz 随切触点CC 的位置及环形铣刀的走刀方向不同，其坐标轴方向不断变化，其中x 轴方向与f方向重合，f 为切触点处沿参数u 方向的单位切向量；z 轴方向与n 方向重合，n 为切触点CC 处参数曲面Σ的单位法向量；y 轴方向与v 方向重合，根据右手法则得到v=n×f，得到v 方向。加工工件局部坐标系CC-xyz 到工件坐标系O-XYZ 的转化矩阵为：

式中：x0，y0，z0—加工工件局部坐标系CC-xyz 下坐标原点CC 在工件坐标系O-XYZ 下的坐标，即加工工件局部坐标系下任一点PL在工件坐标系下的坐标表示PG为：

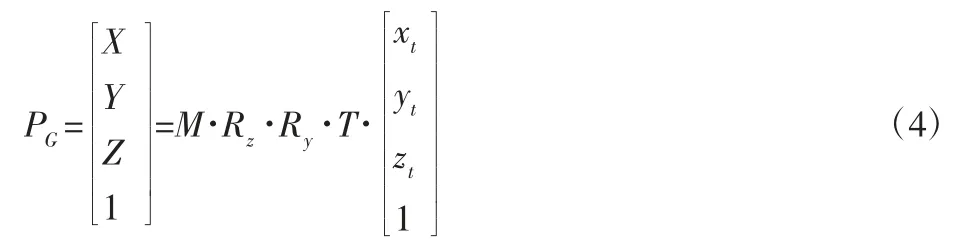
综上所述刀具坐标系中的任意点坐标变换到工件坐标系中对应点PG坐标表示为：

3 构造环形铣刀的刀具包围盒

环形铣刀模型，如图2 所示。在环形铣刀的上表面依次取四个点 P1、P2、P3、P4，其中点 P1、P3在刀具坐标系下的投影点在 yt轴上，点P2、P4在刀具坐标系下的投影点在xt轴上，环形铣刀圆柱上表面中心点为P5，环形铣刀圆柱面下表面的中心点为P6。此外向量i1、i2、i3、i4分别为点 P1、P2、P3、P4指向环形铣刀圆柱上表面中心点 P5的方向向量，i5为环形铣刀圆柱面下表面的中心点P6指向环形铣刀上表面中心点P5的方向向量，i6为环形铣刀上表面中心点P5指向环形铣刀圆柱面下表面的中心点P6的方向向量，将刀具坐标系中的六个点及六个方向向量经坐标变换从刀具坐标系CL-xtytzt下变换到工件坐标系O-XYZ，在工件坐标系中对应的六个点分别为 P1G、P2G、P3G、P4G、P5G、P6G，六个方向向量分别为 i1G、i2G、i3G、i4G、i5G、i6G。

环形铣刀的刀具包围盒，如图3 所示。其分别以构造的六个方向向量i1G、i2G、i3G、i4G、i5G、i6G为平面法向量且分别经过点 P1G、P2G、P3G、P4G、P5G、P6G构造六个平面分别为π1、π2、π3、π4、π5、π6，这六个平面形成一个封闭的长方体，将环形铣刀的圆柱面包围形成环形铣刀的刀具包围盒。

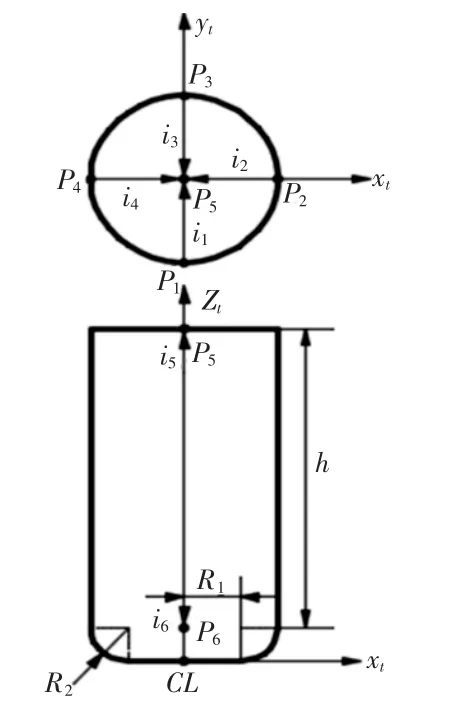
图2 环形铣刀模型Fig.2 Ring Milling Cutter Model

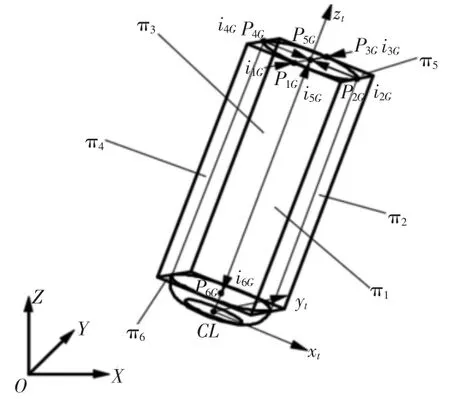
图3 环形铣刀刀具包围盒Fig.3 Ring Milling Cutte Bounding Box

4 参数曲面的网格离散

被加工曲面Σ的参数方程为：r=（u，v），自变量 u，v 为加工参数曲面Σ的参数，（u，v）∈D 并且有参数 u∈［0，1］，v∈［0，1］。在被加工参数曲面Σ上，u曲线和v 曲线构成了参数曲面Σ上的参数曲线网，其中u 曲线和v 曲线的交点构成被加工曲面Σ的离散网格点。将参数曲面Σ的参数域D 沿u，v 方向都进行N 等分，则沿着参数u 和参数v 方向的步长为Δt=1/N，如图4 所示。给定参数域D 中的任一点（ui，vj），都有曲面Σ上的一点r（ui，vj）与之对应，如图4（b）所示。其中（ui，vj）=（u0+iΔt，v0+jΔt），且（u0=0，v0=0），（i=0，1，2，…N；j=0，1，2，…N），对应参数曲面Σ上的点r（ui，vj）=r（u0+iΔt，v0+jΔt）。

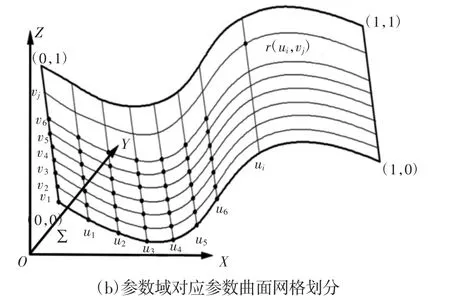
图4 参数曲面的网格离散Fig.4 Mesh Discretization of Parametric Surfaces

5 全局干涉检测算法

环形铣刀的刀具包围盒的上表面π5与下表面π6截取加工参数曲面Σ上的曲面区域为Σ1，如图5（a）所示。设Q 为加工曲面Σ的参数域D 中的任意一网格离散点对应加工曲面Σ上的点，且连接P5G与Q 构成P5GQ 向量，再连接P6G与Q 构成P6GQ向量，则加工曲面Σ上的网格离散点Q 在参数曲面Σ1上需满足的条件为：

根据式（5）确定参数曲面Σ1对应的参数域为 D1，如图5（b）所示。设Q1为参数域D1中的任意参数点对应参数曲面Σ1上的曲面点，则Q1在刀具包围盒中需满足的条件为：

刀具包围盒与加工曲面Σ相交截取加工曲面Σ的区域为Σ2，满足式（6）的加工曲面Σ上的网格离散点在Σ2中，其对应的参数域为D2，设Q2为曲面Σ2上的任一点，经坐标变换在刀具坐标系下Q2点坐标变为Q2t（x0，y0，z0），刀具全局干涉发生条件：

通过式（7）确定刀具与加工曲面Σ发生全局干涉的区域Σ3，其对应的参数域为D3。设Q3为曲面Σ3上的任一网格离散点，且到刀轴线段P5GP6G的距离为d，根据文献[9]计算空间点到线段的距离d，则环形铣刀的最大干涉量Dmax满足下式：

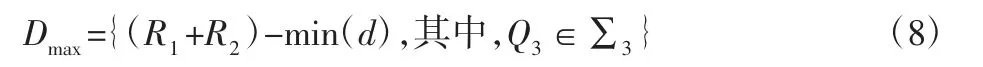
图5 刀具包围盒与参数曲面Fig.5 Tool Encircling Box and Parametric Surface

6 实例计算及其分析

自建三次NURBS 加工曲面模型，如图6（a）所示。采用环形铣刀对工件进行端铣精加工，给定环形铣刀的刀底圆半径R1=4mm、切削刃圆角半径R2=2mm 及刀杆长度h=75mm，给定参数曲面∑网格划分的分割段数N=100，考虑加工效率及局部干涉影响[10]，给定环形铣刀的初始前倾角λ=15°，摆转角ω=0°，环形铣刀的刀触点在参数曲线r（u，0.1）上，将参数曲线r（u，0.1）等参数离散为1000个刀触点。应用VC++6.0 对这里的算法编程求解，进行环形铣刀全局干涉离线检测，得到环形铣刀的最大干涉量曲线图，如图6（b）所示。进一步通过仿真软件Vericut 进行仿真加工，如图6（c）所示。给定前倾角λ=15°，摆转角ω=0°，进行仿真加工在切触点Qcc（0.390，0.10）处第一次出现全局干涉且最大干涉量为0.437mm，由图6（b）可知在u=0.390 处对应最大干涉量为0.443mm，误差在精度要求内满足，证明算法可以精确检测干涉。

图6 NURBS 曲面五轴加工干涉检测Fig.6 Interference Detection of Five Axis Machining of NURBS Surface

7 结论

针对环形铣刀五轴数控加工复杂曲面的全局干涉检测问题，首先将加工曲面沿参数方向进行网格划分得到若干离散网格点，然后用六个平面包围环形铣刀的圆柱面形成包围盒。对于加工参数曲面网格离散点通过计算数量积判断是否在环形铣刀的包围盒内，对落入刀具包围盒的离散点进一步通过网格离散点到刀轴线段的最短距离是否小于刀具半径判断是否存在全局干涉。与传统方法相比这里的算法减少了曲面离散点到刀轴线段距离的计算次数提高了检测效率，该方法解决了基于距离的干涉算法效率低的问题，研究成果有广泛的实际应用前景。