传递矩阵法分析FBG 加速度计的动态性能

仇 磊 ，梁 磊 ，蔡彦璞 ，王 慧

（1.武汉理工大学光纤传感技术国家工程实验室，湖北 武汉 430070；2.武汉理工大学工程结构与力学系，湖北 武汉 430070）

1 引言

加速度计通过测量载体的加速度及其频率进行健康诊断，是结构、设备健康监测中的重要测量元件[1-2]，而基于FBG 的加速度计由于FBG 所具有的抗电磁干扰、长期稳定性好、具有良好的复用功能等优点[3]，在加速度计的研究领域占有一席之地。

常见的FBG 加速度计有膜片式、梁式以及铰链式等。膜片式FBG 加速度计[4-6]是通过质量块运动带动膜片运动，使用FBG测量膜片的应变或者膜片中心的位移来达到测量加速度的目的。梁式FBG 加速度计[7-8]通过质量块运动给梁施加一个惯性力，使用FBG 测量梁的应变或者梁端部的位移达到测量的目的。梁式加速度计受制于梁本身的振动特性，适用于低频加速度的测量。铰链式FBG 加速度计的质量块绕着铰链旋转，将铰链的转角位移转换为FBG 的线位移来测量加速度[9]。将单向柔性铰链扩展为双向柔性铰链，使质量块具有两个运动自由度，可以设计出二维FBG 加速度计[10]。

对于多柔性铰链FBG 加速度计，从理论上分析了其力学传递关系并建立了传递矩阵法模型。通过传递矩阵法分析设计了一种加速度计并制作了一批样品。通过标定实验测试了加速度计的灵敏度与固有频率，验证了模型的正确性。

2 加速度计振动力学模型

FBG 加速度计包括一只FBG，两种不同尺寸的柔性铰链，两种不同尺寸的质量块以及一个基座，如图1 所示。质量块与质量块、质量块与基座之间通过柔性铰链连接，FBG 固定在质量块M2之间。

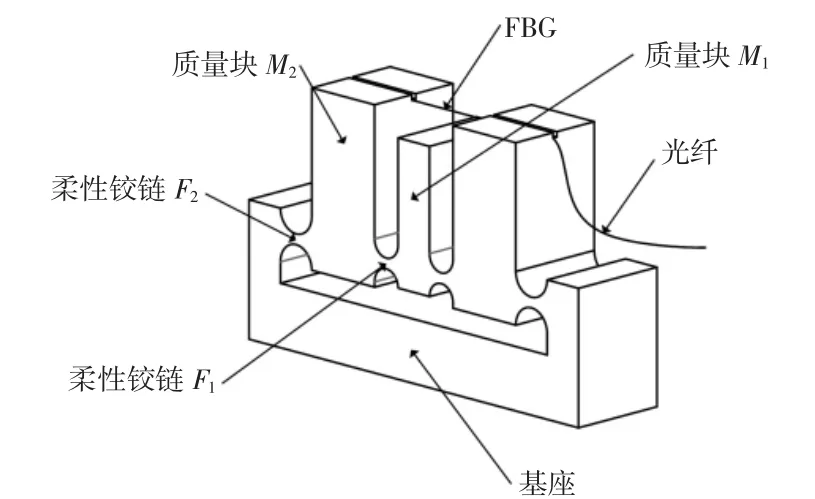
图1 FBG 加速度计结构示意图Fig.1 Structure Schematic of the Accelerometer

在传递矩阵法的分析中，首先将整个结构离散化，分解成一系列具有简单力学特征的二端元件（柔性铰链和质量块），用传递矩阵表示各个元件一端的广义力与广义位移和另一端的广义力与广义位移之间的关系。然后根据元件的排列顺序，经过每个元件的传递，就可由整个系统一端的广义力与广义位移得到另一端的广义力与广义位移。最后根据边界条件即可得到系统的频率方程。

设第i 个截面的状态矢量为：

式中：xi，yi，βi—截面 i 的轴向位移、剪切位移和转角位移；Ni，Qi，Mi—截面i 的轴力、剪力和弯矩。

2.1 FBG 的传感原理与力学模型

当一束宽带光通过FBG 时，满足布拉格条件的光会被反射回来，通过解调仪可以检测到反射光的中心波长（λB）。当FBG 产生均匀变形时，光的中心波长变化量（δλB）与 FBG 应变（ε）之间满足：

粘贴好的FBG 可以被简化为一个弹簧，其刚度可表示如下：

式中：Af—FBG 的横截面面积；

Ef—FBG 的弹性模量；

l—FBG 粘贴点之间的距离。

2.2 柔性铰链的传递矩阵

与质量块相比，柔性铰链尺寸较小，忽略其质量影响。柔性铰链的受力示意图，如图2 所示。柔性铰链的切割半径为R，最小切割厚度为t。

图2 柔性铰链受力示意图Fig.2 Force Diagram of Flexible Hinge

设由柔性铰链左侧传递到柔性铰链右侧的传递方程为：

由文献[11]，柔性铰链的柔度可表示为：

式中：E—材料的弹性模量；

b—加速度计的厚度；

f1，f2，f3—与参数 s=R/t 有关的函数，其表达式为：

柔性铰链右侧截面的位移可表示为刚体位移与变形体位移之和：

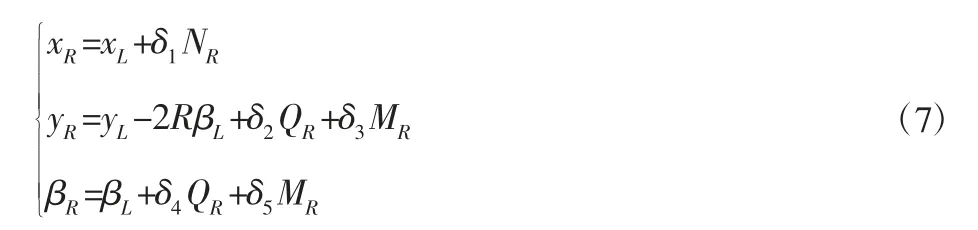
由柔性铰链的平衡条件可得：

联合式与式，柔性铰链的传递方程表示为：

2.3 质量块的传递矩阵

与柔性铰链相比，质量块的尺寸大，变形可以忽略，可以将其视为平面刚体。质量块的受力示意图，如图3 所示。其中，C 点为质量块的质心。质量块的运动可以描述为随o 点的平移和刚体的转动。

图3 质量块受力示意图Fig.3 Force Diagram of Mass Block

设由质量块左侧传递到质量块右侧的传递方程为：

C 点的位移与A 点的水平位移可由左侧截面的位移表示为：

用左侧位移表示右侧位移，可得：

由质量块的平衡条件可得：

式中：F—FBG 产生的力；XC，YC，MC—质量块的惯性力，其表达式为：

式中：m、JC—质量块的质量和绕C 点的转动惯量；ω—质量块的角速度；k—FBG 的刚度，对于不与FBG 相连的质量块，将k设为0 即可。

综合上式，质量块的传递方程表示为：

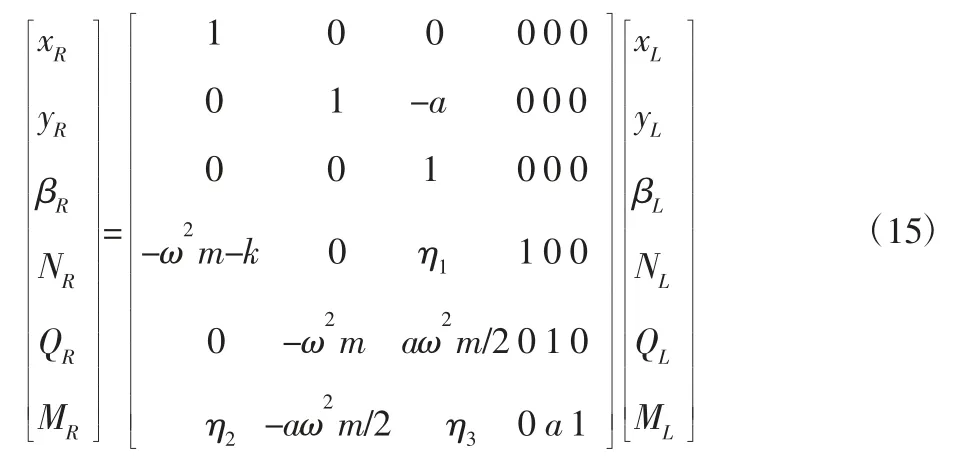
其中参数 η1，η2，η3的表达式表示为：

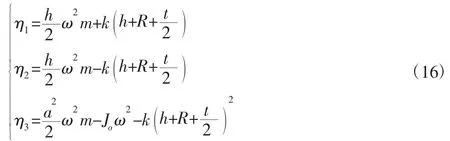
式中：Jo—质量块绕o 点的转动惯量。

2.4 加速度计系统传递方程

设第i 个元件（柔性铰链或质量块）的传递方程为：

根据连续性，第i 个元件左侧状态矢量与第i-1 个元件右侧状态矢量相同：

根据传递性，系统的传递方程可表示为：

3 加速度计动态性能分析

3.1 固有频率分析

考虑到加速度计的基座变形很小，基座与柔性铰链的相交面可以认为没有位移：

将式代入式，可以得到如下方程：

式中：V—一个3×3 的矩阵。

通过矩阵V 的行列式为零即可求得系统的固有频率。

3.2 频率响应分析

设加速度计受到频率为ω，幅值为1g 的简谐加速度作用，加速度计将以同样的频率ω 做简谐振动，即可求得加速度计的频率响应。当ω 为0 时所得的响应为其静态响应。

为了考虑加速度的影响，截面i 的状态矢量扩展为：

柔性铰链的传递方程可以扩展为：

质量块的传递方程可以扩展为：

此时，式变为：

式中：V′—一个 3×4 的矩阵。

通过求解式，可以求得N、Q、M，也就是边界上的状态向量，然后可以求得FBG 的响应。

4 实验结果与讨论

为了验证该种加速度计的动态性能以及传递矩阵分析方法的正确性，我们选择的尺寸加工了加速度计并进行了测试，如表1 所示。

表1 实验加速度计尺寸表Tab.1 Size of the Experimental Accelerometer

将制作好的加速度计固定在振动台上，通过标准压电加速度计给振动台施加幅值为1g，不同频率的简谐加速度，得到FBG加速度计的频率响应曲线。

加速度计的加速度灵敏度频率响应曲线，如图4 所示。传递矩阵法算得固有频率约为1950Hz，实验测得固有频率约为1850Hz。根据传递矩阵法，加速度计的灵敏度高于29.7pm/g。由实验测得加速度计的灵敏度高于26pm/g。

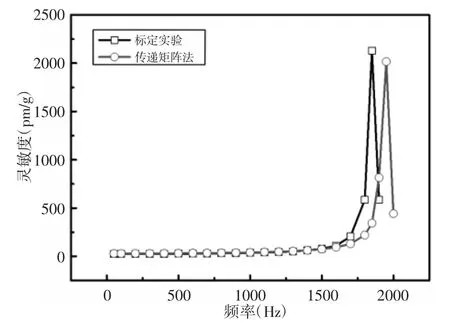
图4 加速度计频率响应曲线Fig.4 Frequency Response of the Accelerometer

5 结论

对于链式柔性铰链FBG 加速度计，通过离散化建立了其每一元件的振动力学模型，推导了加速度计传递矩阵法计算公式。同时制作了加速度计样品，在标准振动台上测试传感器的动态性能。测试结果表明，加速度计的固有频率约为1850Hz，灵敏度高于26pm/g。实验结果与理论分析结果较好吻合，验证了理论分析的正确性。