内燃机各缸功率损失的代理模型诊断方法研究

张艺宝，黄 燕，王 群，闫 兵

（西南交通大学机械工程学院，四川 成都 610031）

1 引言

在内燃机工作过程中，往往由于单个、多个气缸漏气或喷油故障等问题使各缸做功不均匀，扭转振动加剧，对内燃机工作的可靠性、稳定性产生很大影响，严重时会造成整个机组无法正常工作[1]。因此有必要对内燃机的工作状态进行监测和故障诊断。现阶段典型的内燃机做功故障诊断方法主要包括：排气成分及温度监测法[2]，测试气缸压力诊断法，缸盖、机组振动诊断法[3-5]，瞬时转速波动诊断[6-7]，扭矩、气缸压力估计法[1]，噪声检测法[8]等。其中排气成分及温度监测法与测试气缸压力诊断法，均需逐缸测量，对缸数较多的内燃机来说，检测周期长，且不适合在线测量。缸盖、机组振动诊断法与瞬时转速诊断法，优点在于不涉及内燃机结构参数，只需提取故障特征信号进行故障识别，但在多缸失火等复杂情况下，难以保证故障判断和定位的准确性。扭矩、气缸压力估计法，利用瞬时转速反算扭矩或气缸压力，对故障判断的可靠性较高，但诊断结果误差与轴系参数准确度密切相关，需要一套较为精准的动力学模型，噪声检测受环境干扰较大。为克服上述方法中存在的不足从而实现简易、准确的在线各缸功率监测，在FS诊断方法[1]的基础上，采用代理模型替代实际轴系，代理模型具有计算量小，计算周期短，不降低模型精度等特点已广泛运用于多学科的优化设计上[9]，将代理模型引入到内燃机各缸功率损失诊断中，仅利用测试瞬时转速波动信号就能准确定位和反映各缸功率损失程度，既不涉及内燃机结构参数也无需大量的检测工作。对此方法进行了充分的理论分析和反算验证，以证实该方法的可行性和实用性。

2 内燃机做功不均匀代理模型建立基本理论

2.1 内燃机各缸做功与轴系响应基本原理

内燃机运行时，轴系会受到周期性变化的切向力矩，基于内燃机动力学的基本理论[10]，对于多缸机，轴系在某缸切向力矩作用下发生某一振型的振动时，轴系的第v 次简谐扭转振动可表示为[10]：

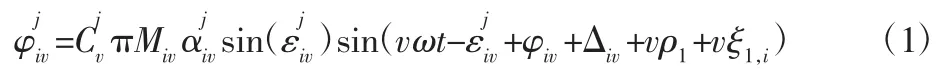
按照线性叠加原理，一个复杂的振动系统可以分解为许多模态的叠加，对于第i 缸第v 谐次来说，该谐次激振力的角位移响应可由其各阶模态响应叠加，如式（2）所示。

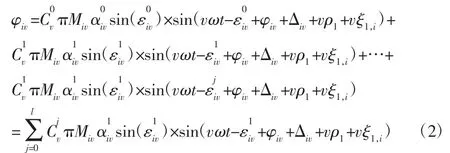
式（2）表明，扭振测点的某缸第v 次简谐扭振角位移是该缸各阶模态的叠加，其圆频率为vω，设幅值为Biv，相位为εiv（以触发始点为基准），可简化为如下关系式：

基于时间求导得到角振动速度的关系式为：

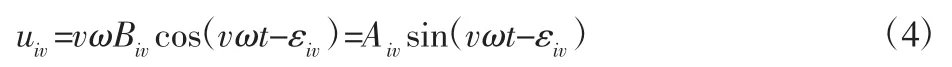
则由n 缸引起的扭转测点总响应为：

由式（2）、式（4）和式（5）可知，多缸机测点的简谐角振动速度与各缸力矩幅值、相位特性间有着确定的函数关系。如果某缸因出现漏气或喷油嘴堵塞等故障而导致气体压力下降，该缸简谐振动速度幅值将随着简谐力矩的减小而减小，测点合成后的扭振角速度幅值必然发生相应的变化。由式（2）还可看出，故障缸的力矩损失不会影响其他缸的角振动速度。因此，如果得到测点的简谐角振动速度将其分解为各缸各谐次简谐力矩的响应，就可以利用上述关系分析内燃机各缸力矩各谐次的特性，进行各缸做功故障诊断。

2.2 谐次选择

对于n 缸内燃机而言，若利用关系式求解各缸的做功不均匀性，至少需要n 个谐次的关系式。基于内燃机动力学理论[10]可知，针对n 缸四冲程内燃机，其发火间隔角为720°/n，简谐力矩相位会出现以n 为周期的重复，如图1 所示。图中K代表各谐次数，该四冲程六缸机每经过6 个谐次，简谐力矩出现周期性循环，因此n 缸机在选择瞬时转速的谐次进行故障缸诊断时，可选取各缸简谐力矩引起测点的角振动的前n 谐次，例如对于四缸机，可选择前四个谐次（0.5、1.0、1.5、2.0 谐次），六缸机选用前六个谐次，八缸机选用前八个谐次。基于谐次选择原理，对于n 缸机，前n 个谐次简谐力矩的角速度响应关系式可表示为：

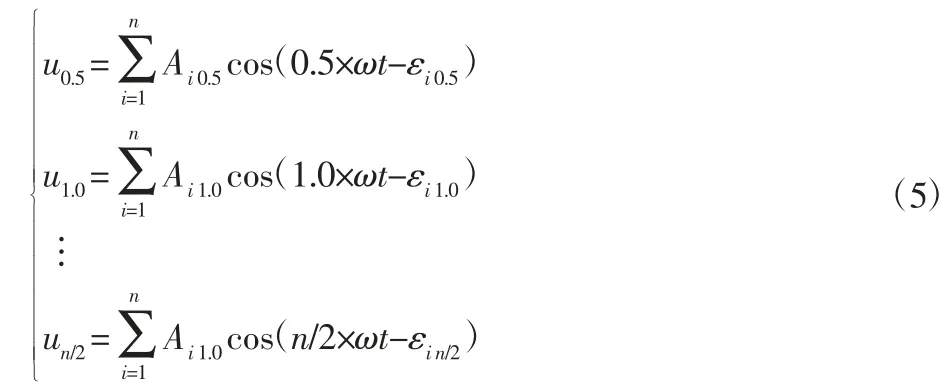
式（5）中共计n 个关系式，每个关系式之间相互独立，且均包含了各缸力矩对角速度的影响，理论上可用于n 缸内燃机做功不均匀性问题的求解。

图1 四冲程六缸机各个谐次相位关系图Fig.1 Harmonic Phase Diagram of Internal Combustion Engine with Four Stroke Six Cylinders

2.3 各缸做功不均匀代理模型理论

由式（2）、式（4）分析可知，测点角振动速度各谐次成分的幅值与相位角是由各缸对应谐次简谐力矩幅值、简谐力矩初相位、发火间隔角、力矩与角振动位移的相位差、振型、触发始点位置等因素决定的。如果直接利用该关系式进行功率诊断，其需要的轴系参数多且不易获得，计算量大，计算周期长，不利于快速识别。代理模型可作为解决上述问题的可行方法，该方法是在满足工程需求精度下，构造一个计算量小，计算周期短，计算结果与物理试验结果相近的数学模型代替实际系统。基于前面诊断理论的研究，该代理模型构造过程如下：

建立各单缸功率损失与各谐次转速幅值关系的数学模型，通过均匀试验设计原则，在设计空间中确定模型所用样本点的位置均布在设计空间，可设置样本点为：单缸功率损失分别为100%、75%、50%、25%、0%，其他缸均正常工作，共计4n+1 种工况为样本点，其中n 为缸数。设内燃机正常工作时由第v 次简谐力引起的角速度响应为，第n 缸不工作其他缸正常工作时由第v次简谐力引起的角速度响应为，第n 缸单缸功率有损失其他缸正常工作时由第v 次简谐力引起的角速度响应为，则单缸功率损失对测试点角速度响应的影响为利用试验方法确定系统在各样本处的响应值构造成一系列样本对，以样本对为基础，寻找一个适合的数学近似模型fiv（xi），其中xi为第i 缸功率损失，使得fiv（xi）与符合得最好。通过上述方法找出合适的数学近似模型式（6）代替式（5），得到各单缸前n 谐次的功率损失代理模型如下：

由式（5）可得知：

将式（7）带入式（6）整理得：

由此，将测点的扭振角位移分解为各谐次切向力矩作用下的角位移响应uv，取前n/2 阶谐次，代入式（8）代理模型关系式中便可求解出各缸的功率损失x1、x2…xn。

在实际进行内燃机各缸功率试验时，单缸完全停缸能够准确实现，但单缸功率损失率难以精确控制（如设置功率损失为50%，实际功率损失可能在（40～60）%内），因而造成设置功率损失与实际功率损失不匹配的问题，使得样本失去准确性。对于该问题可根据参考文献[11]中提出的利用0.5 谐次扭振位移幅值判断出内燃机故障缸的停缸率方法，根据0.5 谐次扭振位移幅值能够准确判断出单缸功率损失，为代理模型提供准确的样本对数据。

3 代理模型的建立

现阶段无法通过简单的方法预先确定在某一工况下各缸真实功率损失，而通过试验的方式判断代理模型的精度又较为困难[1-7]。对于该难点，采用某内燃机轴系的当量模型产生样本数据进行代理模型的构建，通过当量模型随机设置的各缸功率损失与代理模型反算功率损失对比验证代理模型的准确度。某内燃机车四冲程六缸柴油机轴系当量模型，如图2 所示。

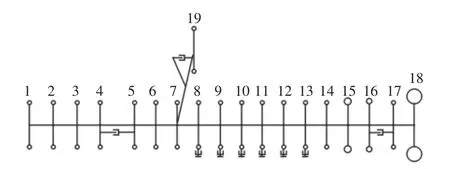
图2 柴油机轴系当量模型图Fig.2 Equivalent Model Diagram of Diesel Engine Shaft System

惯量 1、2 为静压泵，3 为万向轴，4、5 为弹性联轴器，6 为皮带轮，7、19 为减振器部分，8-15 为柴油机部分，16、17 为弹性联轴器，18 为电机转子。该内燃机曲轴自由端扭振试验幅值与当量模型计算幅值对比，如图4 所示。试验与仿真计算得到的综合幅值及主要各谐次幅值随转速的变化规律基本一致，如图3 所示。扭振幅值大小基本相同，各谐次最大误差仅为0.028°，能够满足国标《GBT 15371-2008 曲轴轴系扭转振动的测量与评定方法》[12]中对仿真模型精度的要求。验证了该当量模型的准确性，同时也验证了内燃机各缸各谐次做功与轴系响应叠加原理的正确性。

图3 仿真计算与实测幅值对比Fig.3 Amplitude Comparison Between Simulation and Measured

根据代理模型的建立方法，利用当量模型分别计算出某转速下25 种工况的瞬时转速曲线。1000r/min 下内燃机第一缸功率损失100%工况，一个工作循环对应瞬时曲线图，如图4（a）所示。通过傅里叶变化后取前六个谐次的实部幅值，如图4（b）所示。1000r/min 下内燃机第一缸功率损失对应0.5 谐次转速实部幅值，如表1 所示。

图4 1000r/min 下瞬时转速数据Fig.4 Instantaneous Speed Data at 1000r/min

表1 内燃机第一缸功率损失对应0.5 谐次转速实部幅值Tab.1 The Amplitude Speed of 0.5 Harmonic with the Power Loss of the First Cylinder of the Internal Combustion Engine

同理，可得到其它缸功率损失对应前6 个谐次样本数据，利用样本数据建立多项式响应模型，其数学表达式，如式（9）所示。

式中：xi—m 维自变量 m 的第 i 个分量；β0，β1，βij—未知参数，将它们按照一定的次序排列，可以构成列向量β，求解向量β即可构造出该代理模型。

在代理模型构造中单缸功率损失为自变量xi，该自变量是一维变量，每一缸均有五个试验样本点，最高可得到4 次的多项式响应面模型。为构造精确且次数不高的响应面多项式，需验证各个多项式中各项的重要性，以第一缸功率损失响应多项式为例，利用最小二乘法分别构造出一次，二次，三次，四次多项式，基于R2准则检验不同次项拟合精度，如表2 所示。

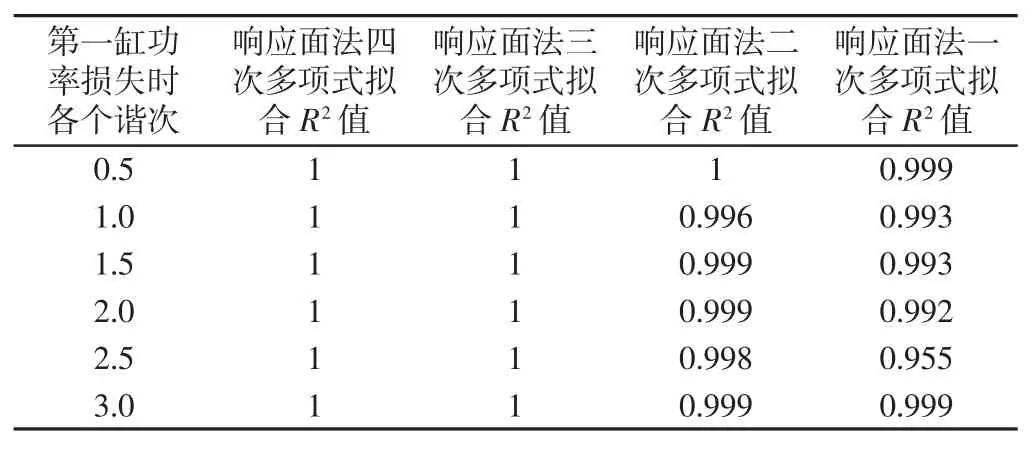
表2 多次项拟合精度R2 值Tab.2 R2 Values of Multiple Fitting

从表2 中可以看出一次项的重要性最大，用最小二乘法三次拟合的R2值已经为1，与各个样本点能够完全重合，因此采用三次多项式构造代理模型，得到1000r/min 下该内燃机做功不均匀响应面代理模型，如式（10）所示。

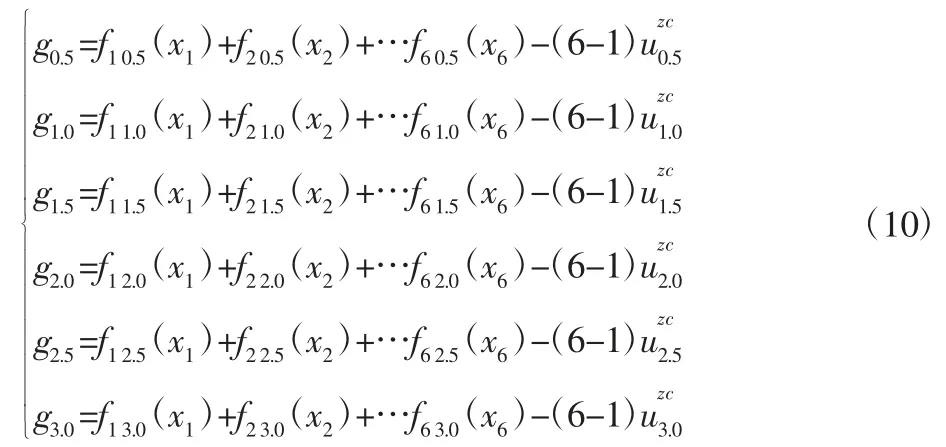
表3 代理模型 Aiv，Biv，Civ，Div 取值表Tab.3 Value of Agent Model of Aiv，Biv，Civ，Div

表4 代理模型取值表Tab.4 Value of Agent Model of

表4 代理模型取值表Tab.4 Value of Agent Model of

谐次（v） 0.5 1.0 1.5 2.0 2.5 3.0 uzcv -0.025 -0.0025 0.0147 -0.0014 0.0492 -0.1496

4 代理模型准确度检测

内燃机各缸做功不均匀工况是无限多的，无法一一对其进行准确度检测，蒙特卡洛思想[13]为检验准确度提供了一种方法。基于该思想，设内燃机各缸功率损失以1%为梯度，各缸的功率损失在（100～0）%，共计 1.06152×1012个工况，设每个工况出现概率均相同，利用随机数产生5 组工况。模拟计算框图，如图5 所示。给出了5 组随机工况各缸的功率损失与代理模型反算结果，如表5 所示。从表5 中可以看出给定的功率损失与模拟反算出的功率损失相差极小，表明利用代理模型反算精度很高，完全能够满足工程计算需要。

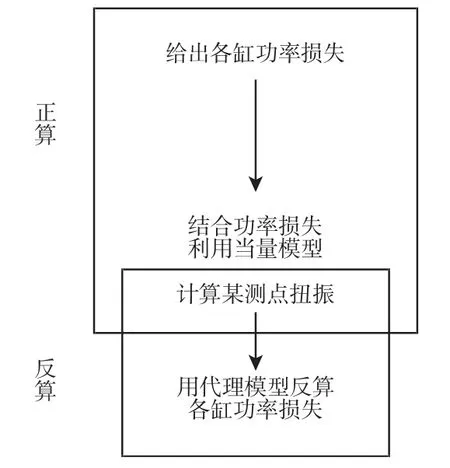
图5 模拟计算框图Fig.5 Diagram of Simulation Calculation

表5 随机工况各缸的功率损失与代理模型反算结果Tab.5 Power Loss in Random Condition of Each Cylinder and the Results of Model

5 结论

针对现阶段典型内燃机做功故障诊断方法的不足，提出了一种各缸功率损失的代理模型故障诊断方法，并基于蒙特卡洛思想进行了反算验证，理论分析和反算验证均证实了该方法的可行性和精确性，主要结论如下：（1）利用瞬时转速的各谐次幅值与功率损失关系建立代理模型原理清楚，有理论依据。（2）基于代理模型诊断内燃机各缸做功故障，不需要内燃机轴系参数模型，可广泛适用于各种机型。（3）通过功率损失反算验证表明：利用新方法反算得到各缸功率损失与给定功率损失相差极小，能够完全满足工程要求，可为快速在线诊断各缸功率损失提供参考。