给除法竖式也摆个小棒图

王亚波

摘 要：任何创造都来源于需要，每一个数学知识都有一个因需要而产生、发展的过程，除法竖式亦是如此。但除法竖式的书写方法与学生熟悉的加减竖式迥然不同，且计算过程涉及除、乘、减三种不同的运算，追根溯源，它的与众不同就是为了能很好地同时表达两种平均分的情况。为了帮助学生从本质上理解除法竖式书写与计算的特殊性，深刻认识除法竖式每一步的含义，我决定延续学生熟悉的加减法竖式中的小棒图，用数形结合的方法教学除法竖式。

关键词：除法竖式;数形结合

一、问题背景

《除法竖式》是新人教课标版二年级下册第六单元的内容，它既是表内除法知识的延伸和扩展，也是今后学习一位数除多位数、多位数除多位数除法的基础，具有承上启下的重要作用。

任何创造都来源于需要，每一个数学知识都有一个因需要而产生、发展的过程，除法竖式亦是如此。为了计算较大数据的加减乘除，我们需要竖式的帮助，但除法竖式的书写方法与学生熟悉的加减竖式迥然不同，且计算过程涉及除、乘、减三种不同的运算，原因何在？难道只是因为约定俗成？那干嘛不约定成加减法的样子，自上而下写，把计算结果写在下面，不是正好一脉相承吗？为什么要倒着写，把计算结果写在上面，还要算出商乘除数的积？所以它的独特必定有着更深层的原因，而这些正是学生心中最大的困惑。

追根溯源，除法的含义是表示“平均分”，而“平均分”的结果存在两种情况，一种是正好分完，没有剩余;另一种是分到最后无法满足平均分的要求，出现剩余。但无论有无剩余，都需要将平均分部分的总量（商乘除数）与被分的总量（被除数）进行比较，除法竖式的与众不同就是为了能很好地同时表达两种平均分的情况。所以，如此复杂的算理、如此精妙的创造绝不能仅用“一除二乘三减”的六字诀简单地把除法竖式的形式强塞给学生。

为了帮助学生从本质上理解除法竖式书写与计算的特殊性，深刻认识除法竖式每一步的含义，体会这个伟大竖式的妙处，经过反复思量和比较，我决定延续学生熟悉的加减法竖式中的小棒图，用数形结合的方法教学除法竖式。

二、情景再现

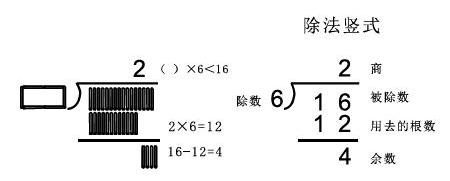
1.搭一个这样的长方形要6根小棒，（板贴）用16根小棒来搭这样的长方形，最多能搭几个呢？判断一下，是有余数的除法还是没有余数的除法？

2. 结果会是什么呢？和你的同桌讨论一下，再用算式表示出来。

谁来说一说你算出来的结果是什么？

生：2个，余4根。

师：还有不同的答案吗？你们列出的算式是？（板书：16

3. 你是怎么想到最多能摆2个长方形的呢？

生：每6根小棒摆一个长方形，我看16里面最多有几个6，二六十二，所以最多能分2个长方形，商是2。

师一边复述一边完成板书：一共16根小棒，（板贴），每六根摆一个长方形，（板贴），能摆几个呢（板书），就看16里最多有几个6？板书（     ）×616，二六十二，最接近16，所以能拼成2个长方形，商是2（板书2）。

4. 商找到了，那又是怎样找到余数的呢？

生2：1个长方形用6根小棒，2个长方形就用了12根小棒。再用16—12就求到多余的小棒。

师边板书边复述：1个长方形用6根小棒，2个长方形就用了12根小棒（板贴）。  我们用商乘除数（板书2×6=12），就求到用掉的根数，再用总的16根减去用掉的根数就求到剩余的根数（板贴，同时板书：16—12=4）

谁能看着小棒图完整地说一说我们找到商和余数的过程。

5.原来我们找到商和除数是经历了这么复杂的思考过程，还有除、乘、减这样三步计算，除了答案，这些思考与计算的过程都不能在横式上表现出来。如果数字变大，981÷23我们算起来会感到很吃力，怎么办呢？（用竖式来算。）对呀，如果我们用数来代替这些小棒，说不定就是一个可以体现除法计算过程的除法竖式呢。我们来试一试。

课件演示对应的替代过程。

16根小棒，每6根搭一个长方形，16里面最多有几个6，商是2，一个长方形用6根小棒，2个就用12根，我们用2乘6求到一共用了的小棒根数，最后用总的16根减去用掉的12根就求到剩余的4根。

（隐去小棒图，）看着它，还能把我们找到商和余数的过程说一说吗？（抽生说）它能体现我们找到商和余数的计算过程吗？（能）。这就是除法的竖式！（出示除法竖式）你能从这个除法竖式中找到被除数、除数、商、一共用了的小棒根数和余数吗？谁上来指一指？

6.教师演示写竖式的过程

我们一起来写一写这个除法竖式：联系横式可以知道应该先写——被除数，再写竖式中的除号，一横一撇。再写除数6，这样就表示出了16除以6。

16除以6商几呢？就看16里最多有几个6，想最接近16的乘法口诀，二六十二，商2。这个2表示2个正方形，所以应该对齐被除数的——（个位）

找到了商，接下来我们就要找找余数了。为了找到剩余的小棒根数，先要找到——用了的小棒根数，所以用2×6，也就是商乘以除数找到一共用了12根小棒，（板书：商乘除数）。最后用总根数减去用掉的根数（板书23—20=3）就求到余数。

7.除法竖式，可以清晰的反应出除法算式中的商和余数是怎样得到的。你们能不能用除法竖式把这两个除法算式的结果求出来呢？

32÷954÷6

抽生上台写。

这个余数是5，这个余数是……为什么这个竖式这儿写的是0呢？师：如果刚好分完，没有余数。我们就写0。

8.除法竖式长得挺奇怪的，为什么不能像加减法竖式那样来书写除法竖式呢？

生1：加减法竖式只能显示出一个结果，而除法竖式既要表示出商，还要表示出余数。

生2：因为要用被除数减去商乘除数的积才能求到余数，所以要把商乘除数的积写在被除数的下面，再在下面算出余数。这一点和减法竖式是一样的。所以商就只能写在被除数的上面了。

三、反思

計算是小学数学教学的主要内容，它贯穿小学数学教学的始终。在计算教学中将抽象的算理直观化，再从直观的算理中抽象出算法，有利于学生真正理解算理，掌握算法，提高能力。

我通过数形结合的方法，用小棒图沟通了平均分过程、求商和余数过程与除法竖式之间的联系，帮助学生理解了商乘除数的由来和作用，理解了除法竖式中每一个数的意义，理解了除法竖式形成的过程;再通过和加减法竖式的比较，进一步明了除法竖式与众不同的独特魅力。由此，化解了学生心中的困惑，形成了对除法竖式的深刻认识。

对除法竖式教学实践的反思，让我体会到数学教学，应该抓住知识的关键点和学生认知中的困惑，努力挖掘支撑它的数学思想，真正触动学生的内心需求，呈现给学生利于建构的学习材料，即使是枯燥的计算教学，都能变得生动形象，让学生在积极主动的探究中获得更加深刻的体验。