数学核心素养观下的动点问题教学研究

陈坛椿，邵为爽

数学核心素养观下的动点问题教学研究

陈坛椿，邵为爽

(齐齐哈尔大学 理学院，黑龙江 齐齐哈尔 161006）

在学生成长的关键阶段，具有良好的数学思维对今后的发展有很大的益处．因此，学生数学核心素养的培养逐渐成为人们关注的热点．动点问题一直是教学的重点和难点，在动点问题的教学中，如何启发学生思维、培养学生的直观想象能力是教学的关键．从培养学生的数学核心素养出发，分析影响学生学习效率的原因，基于教学现状及学生的学习情况，提出相应的解决办法．

动点问题；核心素养；教学策略

数学核心素养是指学生在学习过程中形成的思维能力以及品格素质，主要包括数学抽象、逻辑推理、数学建模、直观想象、数据分析和数学运算等６方面内容[1-2]．在核心素养视角下，学习数学不仅要教会学生如何去做题，更要让学生在数学学习中形成理性的思维方式，培养其创新思维能力．动点问题是指点在几何图形的规定区域内移动，并且在这个过程中存在图形数量关系或位置关系的变化．在动点问题的研究中，离不开数形结合思想．数形结合思想是指将数学里面的理论知识进行一定的转化，以几何图形的方式呈现出来[3]．在解决动点问题的过程中合理运用数形结合思想，可以有效地开发学生的直观想象能力．

当下数学课堂大多仍以说教式教学为主．在动点问题的教学中，虽然有时也会使用现代信息技术，但更多的是通过多媒体来展示习题而不是帮助学生提升他们对知识本质的理解．师生间的互动较少，课堂上留给学生自主讨论的时间有限，在学生讨论后直接公布答案而不是循序渐进地启发学生的思维．这种教学方式很大程度上影响了学生的自主探索能力的培养，导致学生形成模式化的思维方式，学生在听课后，虽然对例题解法有了一定的掌握，但在碰到类似题型时，仍然不能达到举一反三的效果，学生的核心素养很难形成[4]．本文从培养学生数学核心素养的角度，分析动点问题教学中存在的问题，提出相应的教学策略．

1 动点问题教学中常见问题分析

1.1　学习兴趣不高

对于动点问题的学习，学生的反映一直都是太难，不好理解，程度一般的学生在此类题型的测试上只能得到基础的几分，所以对此类型题就产生了惧怕想放弃的心理．在教师讲解此类问题时便失去了兴趣而不去认真的思考，导致对此类问题知识点的掌握严重不足，遇到此类问题时不知道如何解决．所以，如何克服学生对此类问题的恐惧心理，激发学生的学习兴趣，启发学生的解题思路，是动点教学中需要解决的重要问题．

1.2　教学方法单一

数学的灵活度很高，对于一个问题往往有多种解法．但是一些教师却错误地认为，教学时间紧张，学生掌握一种方法可以应对考试就可以了，所以对于许多不同的解法，教师往往不予讲解或者一笔带过[5]．这对学生发散思维的培养是十分不利的，学生在解题过程中不懂得变通，长此以往，这种机械式的教学模式会使学生缺乏对问题的思考，不会举一反三，这也是导致学生进步缓慢的一个重要原因．

1.3　缺少对动点静止状态的体会

在动点问题中，根据题目所给出信息，通常可以归结为考察是否存在某种特殊关系，让学生对这种特殊关系加以证明或者探索在此关系下解的情况，当点运动到满足此类关系的位置时便是我们所要寻找的静止状态．一些教师在讲解此类问题时，常常在分析完题意后便将点的位置直接告诉学生，而学生对点的运动过程却很难想象，在独立解题时不知道如何对运动过程进行形象化处理，常会导致无法求解或者漏解的情况．

2　教学应对措施

2.1　寓教于乐，激发学生兴趣

在课堂教学中，教师应先提出问题让学生表达自己的思路，然后让其给同学讲解知识，这样可以使学生放松心情，紧跟教学思路．在这个过程中，教师要不断地鼓励学生，充分调动其互动性，让学生对讨论充满自信．此外，教师可以适当地让学生按照知识点自编类似问题，让其他同学解答，这样可以对知识有更进一步的理解．同时在编题的过程中，教师可以从学生的自编习题中了解到学生的知识掌握水平，而学生也会逐渐克服对题目的恐惧心理，从而激发学习兴趣，增强学生的学习信心．

2.2　灵活应用翻转课堂，鼓励学生探究多种解法

在教学过程中，教师应探索多种解题方法供学生参考，这样可以很好地将学生的注意力带回课堂．而如何灵活应用翻转课堂，让学生亲身体会多种解法的寻找过程是十分重要的，教师可以将复习内容和对典型例题的解读放在课前的微课中，让学生自学，在课上给学生更多自主讨论的时间．根据学生的不同情况设计分组，在讨论的过程中，可以让学生充分地表达自己的观点，学生不理解的部分教师要进行适当的引导，然后让学生再思考，再引导，……，从而充分地调动学生的思维，让学生自己发掘解题思路，最后再由教师带领学生一起总结梳理，讨论出最简算法．这样，学生在经过反复的思考后，对点的运动轨迹不会再一知半解，可以很好地开阔思维，形成自己的思路和方法（见图1）．

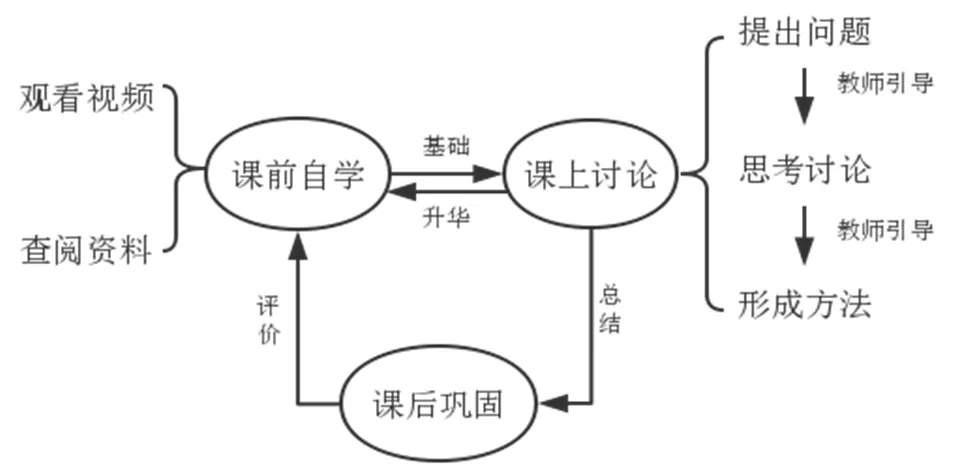
图1 教学环节

在讲授因动点而产生的三角形面积问题时，可以设计教学环节：

2.2.1课前自学选择微课进行预习，教师提前准备２个微课供不同层次的学生选学：一个是复习知识点（二次函数的性质，同底等高的三角形面积相等，平行线间的距离处处相等，同底三角形面积比等于高的比，同高三角形面积比等于底的比）；另一个是割补法求三角形面积的方法．要求学生撰写预习学案，反馈微课中遇到的问题．

2.2.2课上讨论利用投影机展示学生预习学案的完成情况并给予点评．针对学生自学情况及班级人数，设计分组，讨论问题：

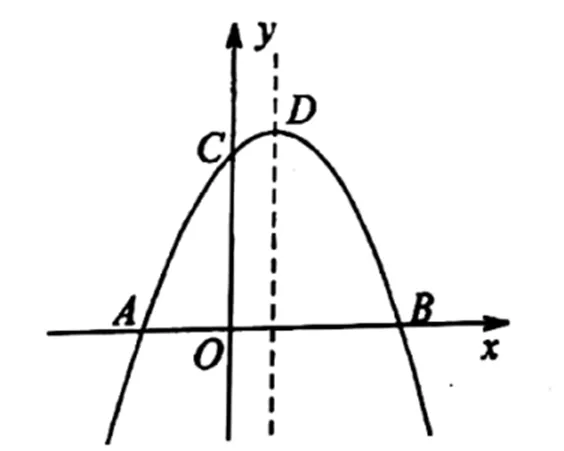
图2 例1图像

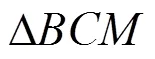
在授课过程中，可以让学生在讨论中自己发现解题思路，从而对题意有更深入的理解，在类似题型中能够灵活运用．

2.2.3课后巩固要求学生课后梳理本节课所学的知识点与解题思路，并设置练习题，让学生小组互评，从而检测学生学习情况并作出相应评价．

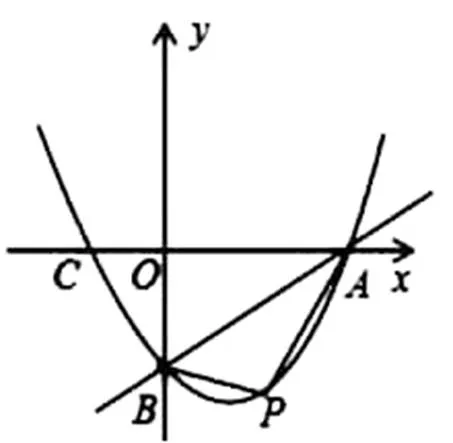
图3　练习题图像

（1）求抛物线的解析式；

能正确将问题完成的学生对此类知识点已充分掌握；仅能做对第１问的学生说明对动点的理解还比较模糊，需要进一步巩固；２个问题都没做对的学生说明基础比较薄弱，课前微课的学习情况较差，需要加强基础知识的练习．

教师在教学过程中要启发学生探索多种解题方法．学生在这个过程中可以深刻感受点的运动过程，从而锻炼学生的自主思维能力，这十分有利于激发学生的学习兴趣，培养学生的数学核心素养．

2.3　引入多媒体，体会运动过程

在动点问题中，对点的静止状态的体会一直是学生学习动点问题的一个难点．多媒体在教学上的应用，为教学的可视化创造了良好的条件，它可以将点的运动情况具体、形象、动态地表现出来，让学生更容易理解和接受．学生通过对图形的观察和判断，从而得出最终的结论．

在探究因动点而产生的特殊三角形个数的问题时，教师可以通过几何画板演示，让学生思考图形的变化．

图4 例2图像

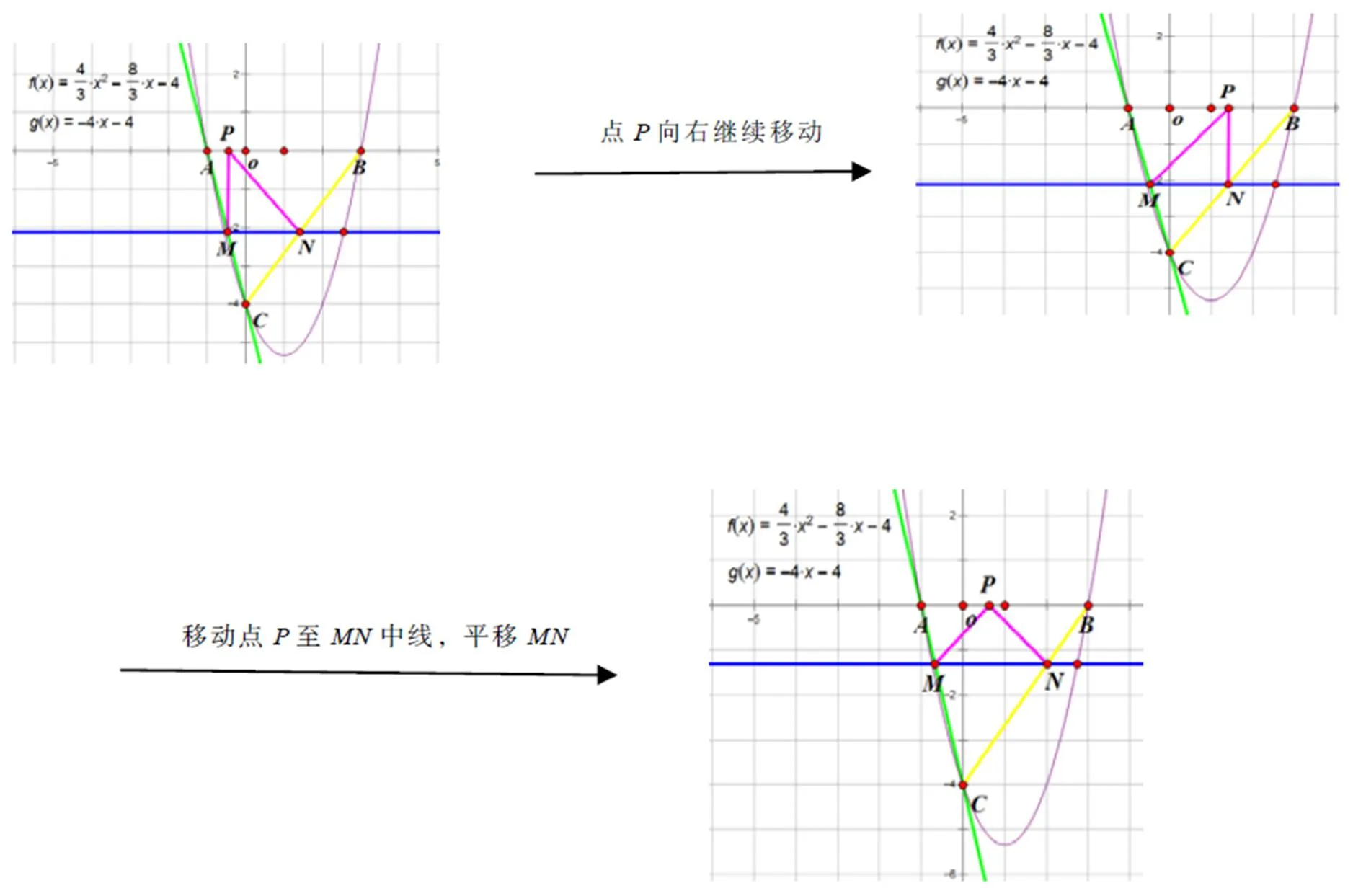
图5　动点轨迹图

3　结语

本文通过分析动点问题的教学现状，发现学生学习兴趣不高，教师教学方法单一及学生无法体会问题实质是影响学习效率的重要原因，教学中注重学生核心素养的培养可以很好地解决此类问题．因此，教师应通过寓教于乐、翻转课堂、应用现代信息技术等方法来激发学生的学习兴趣，锻炼学生的思维，提高学生的直观想象能力．正确掌握培养学生数学核心素养的教学方法，将会获得更好的教学体验，改善教学现状，从而促进学生的良好发展．

[1] 郭天海．核心素养下初中数学高效课堂初探[J]．学周刊，2019（32）：29

[2] 卞红艳．培养数学核心素养促进深度学习探研[J]．成才之路，2018（31）：34

[3] 房金明．初中数学教学中数形结合思想的应用[J]．科学大众·科学教育，2019（9）：26

[4] 郑博文．初中数学二次函数动点问题的教学策略研究[J]．课程教育研究，2019（45）：131

[5] 杨力．从“知”到“智”——初中数学核心素养探究[J]．数学教学通信，2019（32）：41-43

Research on the teaching of the moving point problem under the view of mathematical core literacy

CHEN Tanchun，SHAO Weishuang

（School of Science，Qiqihar University，Qiqihar 161006，China）

At the critical stage of students′ growth，good mathematical thinking is of great benefit to their future development．Therefore，the cultivation of students′ mathematical core literacy has gradually become a focus of our attention．The moving point problem has always been a key and difficult point in teaching，in the teaching of moving point problem，how to inspire students′ thinking and cultivate students′ intuitive imagination is the key to teaching. Starting from the cultivation of students′ mathematical core literacy，the reasons that affect students′ learning efficiency was analyzed．Based on the current situation of teaching and students′ learning，the corresponding solutions was put forward．

moving point problem；core literacy；teaching strategy

O12∶G642.0

A

10.3969/j.issn.1007-9831.2020.06.015

1007-9831（2020）06-0069-04

2020-03-25

黑龙江省高等教育教学改革项目（SJGY20180560）；齐齐哈尔大学学位与研究生教育教学改革研究项目（JGXM_QUG_2018020）

陈坛椿（1996-），女，黑龙江齐齐哈尔人，在读硕士研究生，从事数学教学论研究．E-mail：542432863@qq.com

邵为爽（1980-），女，黑龙江齐齐哈尔人，副教授，从事数据挖掘及数学教育教学研究．E-mail：shaoer720@126.com