小参数对流扩散方程在最优分层网格的一致收敛有限元计算

孙美玲

小参数对流扩散方程在最优分层网格的一致收敛有限元计算

孙美玲

（南通职业大学 公共教学部，江苏 南通 226007）

面向小参数的奇异摄动对流扩散方程，构建分层网格自适应地刻画边界层对应的离散结点，应用有限元计算以期在特殊网格上得到优化结果．分层网格无需复杂计算，仅根据递推关系可形成随机剖分数的优化网格，实现更好地捕捉边界层．数值算例验证了方法的鲁棒性，获得了完全独立于小摄动参数、一致收敛的有限元高精度数值结果．

对流扩散方程；小参数；分层网格；有限元法；一致收敛

奇异摄动问题是当前科学工程计算的热点，广泛地出现在弹性力学、流体计算、生物系统和运筹控制等众多领域．在进行数学物理方程描述时，小参数会作为系数出现在方程的最高阶导数项，精确有效地求解奇异摄动问题渐进解或近似解一直是相关研究的目标[1-2]．但如果常规处理简单地将小参数设为零，将导致原方程降阶从而不能得到所有的近似解．奇异摄动来源于问题存在多个尺度，为了得到每个尺度的有效近似解，可以将方程用不同尺度分解以得到新方程．

本文考虑一维奇异摄动问题

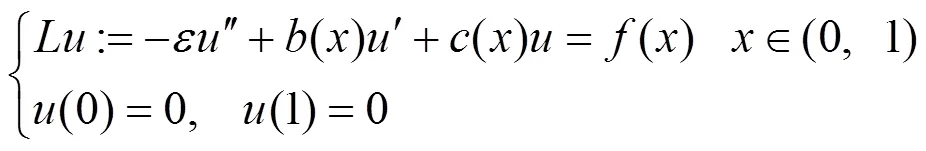
本文研究含小参数问题（1）的精确高效解，应用有限元计算，结合自适应生成的分层网格精确模拟解的边界层部分和光滑部分，得到与真解相比精度非常高、完全独立于摄动系数大小的收敛解．

1　有限元的变分处理

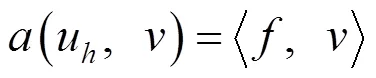
将每一单元形成的单元刚度矩阵累加到所有单元形成总刚度矩阵，求解对应的大规模稀疏线性方程组，即得到有限元数值解．之后还可以对计算结果进行误差分析与后处理，通过列表和画图判断数值结果的精确程度与收敛性，进一步提升方法的校正和改进性能．

2　分层网格的自适应构建

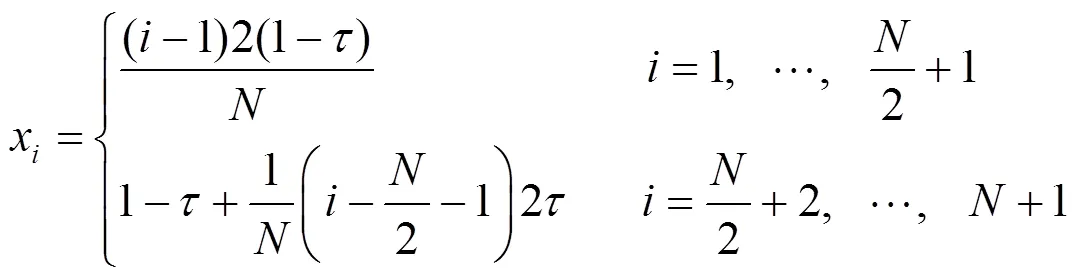
这种分片等距Shishkin网格较之前的分段等距一致网格，能较好地捕捉解的部分奇性．不过Shishkin网格也存在一个缺点，即在某些情形当剖分数为奇数时，可能造成不稳定．

基于一致Uniform网格和Shishkin网格存在的不足，本文给出分层Graded网格（简记G网格）算法．

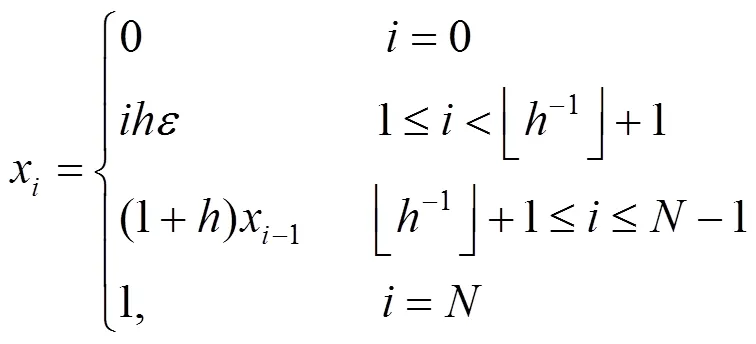
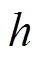
3　程序执行与数值算例

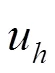
表1　有限元计算在3种网格得到的最大模误差与收敛阶

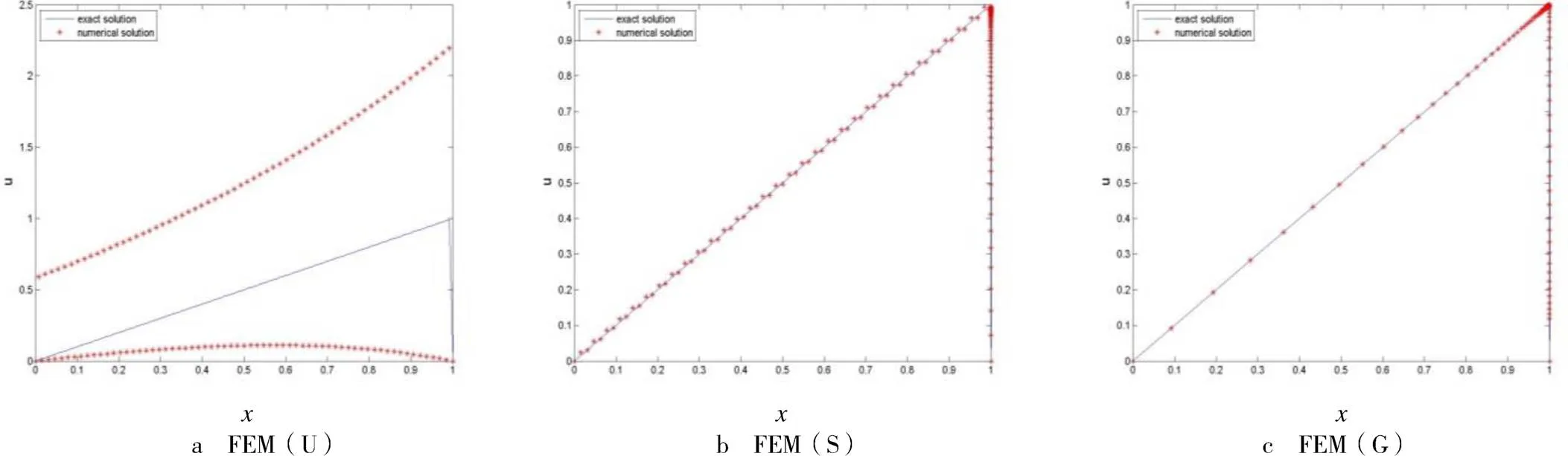
图1　真解与数值解的对比

本文所提方法能正确高效地模拟小参数引起的奇异摄动边界层问题，采用分层网格的自适应生成方案并运用有限元计算，获得了完全不依赖于参数大小且能保证高精度与快收敛的数值模拟结果．

[1] Miller J J，Oriordan E，Shishkin G I．Fitted numerical methods for singular perturbation problems[M]．Singapore：World Scientific，2012

[2] 张伟江，周明儒，林武忠，等．奇异摄动导论[M]．北京：科学出版社，2014

[3] Reddy J N．An introduction to the finite element method[M]．3th ed．New York：McGraw Hill，2006

[4] Roos H G，TeofanovL，Uzelac Z．Graded meshes for higher order FEM[J]．J Comput Math，2015，33（1）：1-16

[5] 王建云，田智鲲．定常非线性薛定谔方程的有限元方法超收敛估计[J]．湘潭大学自然科学学报，2018，40（1）：24-26

[6] Qiu C X，Zhao W J，Song L N．A balanced finite element method of least-squares formulation for singularly perturbed reaction-diffusion problems[J]．Chinese J Engineer Math，2016，33（3）：309-318

[7] Jiang S，Presho M，Huang Y Q．An adapted Petrov-Galerkin multiscale finite element method for singularly perturbed reaction-diffusion problems[J]．Inter J Comput Math，2016，93（7）：1200-1211

[8] Jiang S，Sun M L，Yang Y．Reduced multiscale computation on adapted grid for the convection-diffusion Robin problem[J]．J Appl Anal Comput，2017，7（4）：1488-1502

[9] Chen C J，Chen Y P，Zhao X．A posteriori error estimates of two-grid finite volume element methods for nonlinear elliptic problems[J]．Comput Math Appl，2018，75：1756-1766

[10] 尹云辉，祝鹏，杨宇博．流线扩散有限元方法在分层网格上的收敛性分析[J]．计算数学，2015，37（1）： 83-91

Uniformly convergent finite element computation on optimally graded meshes for the convection-diffusion equation with a small parameter

SUN Meiling

（Department of Public Course，Nantong Vocational University，Nantong 226007，China）

As for a singularly perturbed convection-diffusion equation with a small parameter，a graded mesh is built adaptively to describe the discrete nodes of the boundary layers，and the finite element computation is applied to solve the optimal results on special meshes．The graded mesh is free of complicated operations，it can be realized from a recursive formulation to build the optimal mesh with random partition numbers，which is qualified to capture the boundary layers．The robustness of the method is shown through numerical experiments，the high precision numerical results of finite element are obtained，which are completely independent of small perturbation parameters and uniformly convergent．

convection-diffusion equation；small parameter；graded mesh；finite element method；uniformly convergent

O241.81

A

10.3969/j.issn.1007-9831.2020.06.001

1007-9831（2020）06-0001-04

2020-03-19

国家自然科学基金面上项目（11771224）；南通职业大学自然科学研究项目（1512105）

孙美玲（1981-），女，江苏南通人，副教授，博士，从事微分方程数值解及其应用研究．E-mail：sunmeiling81@163.com