群论中“不变子群”概念的理解

◎朱宽云 杨永伟 （．长江大学 信息与数学学院，湖北 荆州 43403；．安阳师范学院 数学与统计学院，河南 安阳 455000）

一、引 言

近世代数是大学本科数学专业的主干课程之一，主要包括群、环、域三个代数系统．在近世代数视角下，可以清晰地看到很多初等数学内容的本质，这是数学专业师范生的职业技能需求［1］．但是由于近世代数具有高度抽象性和严密逻辑性的特点，学生学习起来往往困难重重．在群论中，不变子群是一类特殊的子群，在商群的构造中起着十分重要的作用，然而对于初学者来说，对不变子群的出现往往感到困惑，构造商群一定需要不变子群吗？ 本文以张禾瑞先生所编的《近世代数基础》教材［2］为参照，采用问题导向的方式，逐步论述在不变子群的基础上构造商群的必然性．同时，讨论了不变子群的定义条件和元素可换的关系，以及不变子群的传递性问题．

二、不变子群的由来

问题1 设H 是群G 的子群，Sl＝｛aH｜a∈G｝为H 的所有左陪集构成的集族，那么Sl关于子集乘法构成群吗？

解析 如果Sl关于子集乘法能够构成群，则Sl中的元素关于子集乘法满足封闭性，即对于任意的xH，yH∈Sl，xH·yH＝zH∈Sl，也就是说左陪集xH 与左陪集yH 的乘积结果必须是一个左陪集．然而，要达到这一要求，须满足下述条件．

引理1 设H 是群G 的子群，∀x，y∈G，

则xH·yH 仍是左陪集⇔∀a∈G，aH＝Ha．

证明 （⇒）对任意的a，b∈G，ba＝（be）（ae）∈（bH）（aH），

故baH＝（bH）（aH）．再根据群的消去律可得aH ＝HaH，因此，∀ha∈Ha，存在h1，h2∈H，使ah1＝hah2，可得ha ＝∈aH，故Ha⊆aH．

另外，根据上述讨论结果可得Ha-1⊆a-1H，

所以aH⊆Ha．综上，aH＝Ha．

（⇐）由于∀a∈G，aH ＝Ha，根据结合律和子群的性质H＝HH，可得

根据引理1 的分析，Sl要关于子集乘法构成群则须满足条件：∀a∈G，aH ＝Ha．这时候可求出Sl的单位元（aH）-1＝a-1H，aH·bH＝（ab）H．

因此，我们可以看出，

Sl关于子集乘法构成群⇔∀a∈G，aH＝Ha．

此时，G 中满足条件∀a∈G，aH ＝Ha 的子群H 就构成了一类新的子群——不变子群（或称为正规子群）．

三、不变子群及其判定

定义1［2］设N 是群G 的子群．若∀a∈G，

例1设G ＝S3，则N ＝｛（1），（1，3，2），（1，2，3）｝是G的不变子群．

问题2 设N 是群G 的子群，a∈G，那么aN ＝Na 与∀n∈N，an＝na 的关系是什么？

答 这里“aN ＝Na”代表aN 和Na 两个集合相等，“∀n∈N，an＝na”代表N 中的所有元素与a 可交换．

（1）显然，当“∀n ∈N，an ＝na”成立时，容易得到aN＝Na．

（2）若aN ＝Na，不妨设an1∈aN，则存在n2∈N 使得an1＝n2a，进一步可得，n1＝a-1n2a．但是，在没有其他条件限制的情况下无法得到n1＝n2．也就是说条件“aN ＝Na”无法保障“∀n∈N，an＝na”是成立的．在例1 中，（1，2）N ＝N（1，2）＝｛（1，2），（2，3），（1，3）｝成立，并且（1，2）（1，2，3）＝（1，3）＝（1，3，2）（1，2），但是（1，2，3）≠（1，3，2）．

（3）G 的中心

是G 的子群，并且G 的任一元a 和N（G）中的任一元n可换，即an＝na，故aN（G）＝N（G）a，所以N（G）是G 的不变子群．对于N（G）来说，可以根据aN（G）＝N（G）a 得到结论“∀n∈N（G），an ＝na”．不妨设an1∈aN（G），则存在n2∈N（G）使an1＝n2a，进一步，由an1＝an2根据群的消去律可得n1＝n2．这里，可以看到由an1＝n2a 推出n1＝n2的关键在于N（G）中的任一元素与群G 中的所有元素是可换的，故“aN＝Na⇒∀n∈N，an＝na”成立．

（4）对于可换群G 的任一子群N，由于∀a，x∈G，总有ax＝xa，所以aN＝Na，故可换群的任一子群都是不变子群．并且N 中的任一元素与G 中的所有元素是可换的，所以结论“aN＝Na⇒∀n∈N，an＝na”成立．

定理1［3，4］（不变子群的判别定理）设N 是群G 的子群，则下列条件等价：

定理1 的前提条件是：N 是群G 的子群，而不是N 是群G 的非空子集．不变子群之所以重要，其根本原因在于这种子群的全体陪集对于子集的乘法可以做成一个新的群．

设N 是群G 的不变子群，将N 的所有陪集做成一个集合S＝｛aN｜a∈G｝，由问题1 的讨论可知，在陪集的乘法下，即∀x，y∈G，

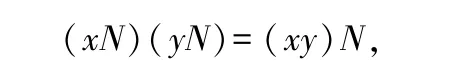
S 构成一个群，将其称为G 关于N 的商群，记作G／N．

四、不变子群的传递性问题

群的不变性与群的可换性在有限群论的研究中扮演着非常重要的角色，而如何利用二者的联系来研究有限群的结构是一个重要的课题．

我们知道“子群”的概念具有传递性：

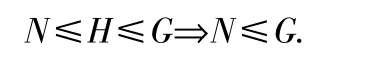
那么“不变子群”是否也具有传递性呢？ 即

例2［5］已知Klein 四元群

是4 次对称群S4的一个不变子群，又因为K4是一个可换群，故其子群

是K4的一个不变子群，从而有

但是B4不是S4的不变子群，因为

（1，3）B4＝｛（1，3），（1，2，3，4）｝≠B4（1，3）＝｛（1，3），（1，4，3，2）｝．

这说明了，不变子群的不变子群不一定是原群的不变子群，亦即不变子群不具有传递性．

例2 同时表明了在非可换群S4中有的不变子群不具有传递性，但并不是所有的不变子群都无传递性．例如，4 次交替群A4是4 次对称群S4的不变子群，Klein 四元群K4是A4的不变子群，即而根据例2 可知，K4是S4的不变子群，即这就论证了非可换群S4中有的不变子群具有传递性．

在一些特殊的非可换群中，不变子群的传递性是恒成立的．例如，Hamilton 群

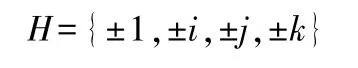
是非可换群，H 的每个子群都是正规子群，因此，对于Hamilton 群H 来说，不变子群的传递性恒成立．

一般地，若一个群G 的任何子群都是不变子群，则称G为Dedekind 群．显然，Dedekind 群G 具有不变子群的传递性的性质．

虽然并不是所有的群都具有不变子群传递性，然而，若添加一定条件，则可以得到下述结论．

定理2［3，4］设G 是群，N≤H≤G．若

证明 对任意的n∈N，h∈H，则h∈G，由N 是G 的不变子群，可得hnh-1∈N．根据定理1 可知，N 是H 的不变子群．