特色小镇PPP 项目利益分配模型研究

（湖南财政经济学院，湖南 长沙 410205）

一、引言

自2016 年10 月，国家发改委颁布《关于加快美丽特色小（城）镇建设的指导意见》（发改规划[2016]2125 号），提出推动创新特色小镇建设投融资机制，大力推进政府和社会资本合作，PPP 模式在特色小镇项目开始推广运用。特色小镇PPP 项目具有建设周期长，投资额巨大，各利益主体合作机制较为复杂等特点。利益成为驱动特色小镇PPP 项目利益相关主体积极参与项目建设的重要动力，而公共部门、私营部门与本土产业作为特色小镇PPP 项目的主要利益主体，三方的参与程度决定项目利益能否实现最大化，因此，构建更为合理、有效的利益分配机制，满足三方利益诉求，成为特色小镇PPP 项目成功的前提和关键。

梳理国内外文献，已有成果基于实物期权-博弈论（RO-GT）模型[1]、修正Shapley 值分配模型[2-5]、关系定性比较分析法（QCA）[6]研究PPP 项目利益分配，但是这些模型均局限于一般PPP 项目公共部门与私营部门双方的利益诉求，并未考量特色小镇PPP 项目的核心利益主体之一本土产业的利益诉求。本土产业作为特色小镇项目发展的核心方，与项目建设息息相关，在项目落实过程中不可或缺，对于项目成果和持续发展有着决定性作用，因此，特色小镇PPP 项目利益分配需要聚焦“公共部门+私营部门+本土产业”三方核心利益主体，构建更合理的特色小镇PPP 项目利益分配模型。

二、特色小镇PPP 项目核心利益主体界定

作为特色小镇PPP 项目核心利益主体，同时是特色小镇PPP 项目全生命周期中最活跃部分，项目主要参与者在项目全生命周期中起到主导作用。其中，公共部门负责制定相关优惠政策并监管特色小镇的建设进程及质量，凭借公信力，调和各利益主体矛盾，建立多利益主体合作机制，推动项目顺利进展与成功；私营企业作为特色小镇开发建设主体，负责对小镇进行综合化建设，对于一些前期阶段难以盈利的基础设施建设承担主要责任；本土产业作为特色小镇项目“特色”，是项目核心生产力，从满足自身利益诉求出发，积极参与公私双方发起的特色小镇项目，负责发展“特色”产业，保障项目持续稳定。

基于此，本文界定特色小镇PPP 项目核心利益主体：公共部门、私营部门与本土产业。“公共部门+私营部门+本土产业”三方核心利益主体是特色小镇PPP 项目不可或缺群体，与项目有着紧密的主动利害关系，对于项目的达成和项目利益最大化的实现至关重要，共同致力于实现项目利益最大化。

三、特色小镇PPP 项目“公共部门+私营部门+本土产业”利益分配模型

假设特色小镇PPP 项目中，包括公共部门、私营部门与本土产业在内的参与利益分配的三方主体，均为追求自身利益最大化的理性人，由此构成合作联盟。该合作联盟成员之间利益活动具有互不对抗的性质，同时，收益与合作主体数量之间并非反比例数量关系。在此形势下，联盟中全员合作将达成最大收益，这种最大收益分配方案可由Shapley值法来估算。

（一）Shapley 值理论

假设合作联盟有n 个参与者，其所有子集G∈I，集合I=（1，2，…，n），任意集合G 都有对应收入V（G），且满足：

若假设设XI为参与者收益；|G| 为参与合作联盟个体数量；ω（|G|）为利益分配权重；V（G/i）为联盟G 去掉参与者i 后的收益；[V（G）-V（G/i）]为成员i对合作联盟作出的贡献；s/i 与n/s 的参与者排列次序有则：（n-|s|）!（|s|-1）!种，则：

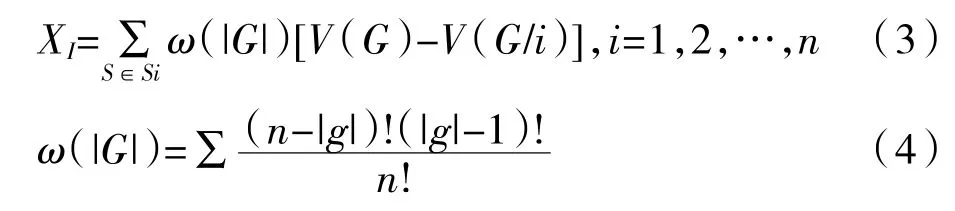
（二）基于三方合作博弈Shapley 值特色小镇PPP 项目利益分配模型

定义特色小镇PPP 项目中公共部门、私营部门与本土产业三者间的合作博弈（N，V），其中N 代表公共部门（J）、私营部门（K）与本土产业（L），V 代表三者不同合作联盟带来的收益。根据Shapley 值法计算公共部门、私营部门与本土产业在单独运作、两两合作及三者共同合作时的利益分配方案，具体利益分配情况如下：

1.公共部门J 的利益分配

表1 公共部门J 利益分配表

表1 详细列出公共部门J 在参与所有合作联盟中所获得的联盟收益：

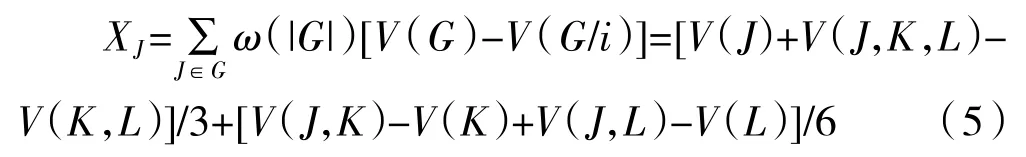
2.私营部门K 的利益分配

表2 私营部门K 利益分配表

表2 详细列出私营部门K 在参与所有合作联盟中所获得的联盟收益：

3.本土产业L 的利益分配

表3 本土产业L 利益分配表

表3 详细列出本土产业L 在参与所有合作联盟中所获得的联盟收益：

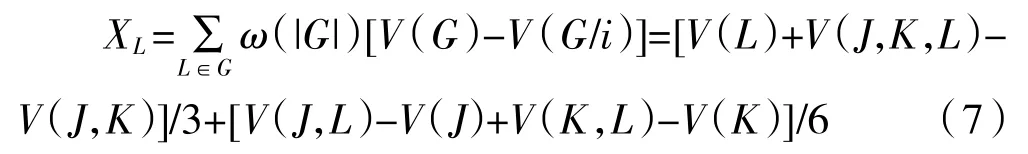
从而通过式（5）、式（6）、式（7）可分别求得在特色小镇PPP 项目合作联盟中公共部门、私营部门与本土产业三方的收益。

（三）基于三方讨价还价博弈模型修正权重的特色小镇PPP 项目利益分配模型

基于特色小镇PPP 项目中三方核心利益主体关系，公共部门处于强势地位，私营部门次之，本土产业最弱，因此，在三方主体都是理性人的前提假设下，为实现利益最大化，最弱势方将与最强势方达成“同盟”，双方互通信息、优势互补，从而在与另一方的博弈中获得更大利益，因此本土产业将与政府部门达成“同盟”。

特色小镇PPP 项目利益分配博弈分为两个阶段。

第一阶段：由同盟与私营部门进行博弈，双方共同对比例之和为1（即ωJ，L+ωK=1）的利益进行权重分配，建立无限期讨价还价模型。

双方在讨价还价博弈中，为获得自身最大利益，会持续消耗一定的成本，如信息获取费用、时间、机会成本等，因此，假设谈判损耗系数δi（δi＞1）。双方地位不同，谈判损耗系数因而不同，优势一方在谈判上的支出往往小于劣势一方，同盟在地位上高于私营部门，故同盟的谈判损耗系数δJ，L小于私营部门的谈判损耗系数δk（即δJ，L＜δk）。

第一轮谈判，私营部门首先提出分配方案，即私营部门利益分配权重ω1，此时同盟的利益权重为1-ω1。同盟的利益分配权重用（J，L）表示，私营部门的利益分配权重用（K）表示，即：

若同盟接受该分配方案，博弈结束；若同盟拒绝该分配方案，进入第二轮谈判。

第二轮谈判，由同盟进行讨价还价，提出新的利益分配权重ω2，但同时，谈判产生损耗，则本轮利益分配权重为：

若私营部门接受该分配方案，博弈结束；若私营部门拒绝该分配方案，再次进入第三轮谈判。

第三轮谈判是私营部门进行还价，本轮提出新的利益分配权重ω3，同时由于谈判的继续进行，继续产生谈判损耗，本轮利益分配权重为：

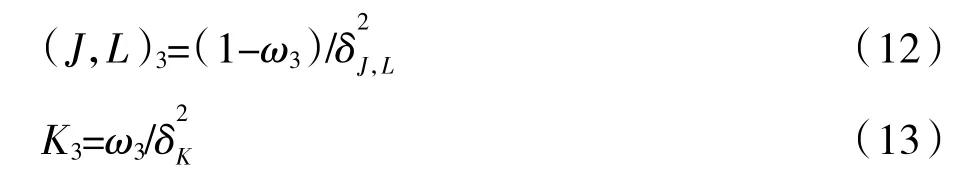
讨价还价过程按上述方式无限循环，直至一方主体接受，博弈结束。

针对无限回合讨价还价博弈模型的求解，本文借鉴学者谢识予（2002）[7]提出的解决方法，即原有博弈方的对立关系不会因为无限次的博弈结果而改变，也可理解为结果不会因设立的逆推基点是第一回合或是第三回合而改变。本文据此选择第三回合作为无限回合谈判逆推初始点，进行以下求解。

在第二轮谈判时，同盟考虑到若提出方案中对私营部门的利益分配权重K2小于第三轮谈判私营部门利益分配权重K3，则私营部门一定会选择进入第三轮谈判而拒绝该方案。因此，为减少不必要的谈判损耗，避免进入第三轮谈判，同盟应在第二轮谈判中保证私营部门此阶段的权重大于等于第三轮谈判的权重，同时争取自己利益的最大化，分配策略应为：

将式（11）、式（13）代入式（14），整理得：

此时，同盟的利益分配权重为：

式（16）为第二轮谈判同盟利益分配权重最大值，并与式（12）进行比较：

因为，1＜δJ，L＜δK，所以（J，L）2＞（J，L）3，故双方都不会选择进入第三轮谈判。

同理，在第一轮谈判中，私营部门同样需要考虑保证在第一轮谈判中同盟权重大于等于其在第二轮谈判中同盟权重，同时争取利益最大化，则：

将式（8）、式（16）代入式（18），整理得：

该博弈模型是无限回合讨价还价模型，其显要特征为，不论是第一回合还是第三回合的开始，其讨价还价的最大权重均一致，因此有：

整理可得：

将式（21）代入式（8）、式（9）可以得出同盟与私营部门的利益分配权重：

第二阶段：由同盟内部公共部门和本土产业进行再博弈，双方共同对比例之和为k（ωJ+ωL=k，k=（δK-1）/（δJ，LδK-1））的利益进行权重分配，建立无限期讨价还价模型。

双方在再讨价还价博弈中，必定也会存在谈判损耗系数εi（εi＞1），且公共部门谈判损耗系数εJ小于本土产业谈判损耗系数εL（εJ＜εL）。

第一轮谈判，本土产业首先提出分配方案，即本土产业利益分配权重α1，此时公共部门的利益权重为1-α1。公共部门利益分配权重用J 表示，本土产业利益分配权重用L 表示，即：

若公共部门接受该分配方案，博弈结束；若公共部门拒绝该分配方案，进入第二轮谈判。

第二轮谈判，由公共部门进行讨价还价，提出新的利益分配权重α2，谈判继续产生损耗，本轮利益分配权重为：

若本土产业接受该分配方案，博弈结束；若本土产业拒绝该分配方案，进入第三轮谈判。

第三轮谈判是由本土产业主导，进行还价，此时更新提出利益分配权重α3，同时由于谈判的继续进行，继续产生谈判损耗，本轮利益分配权重为：

讨价还价过程按上述方式无限循环，直至一方主体接受，博弈结束。

同第一阶段一样，在第二轮谈判时，公共部门考虑到若提出方案中对本土产业利益分配权重L2小于第三轮谈判本土产业利益分配权重L3，本土产业一定会选择进入第三轮谈判而拒绝该方案。为减少不必要的谈判损耗，避免进入第三轮谈判，公共部门应在第二轮谈判中保证本土产业此阶段的权重大于等于第三轮谈判的权重，同时争取自己利益的最大化，分配策略应为：

将式（27）、式（29）代入式（30），整理得：

此时，同盟的利益分配权重为：

式（32）为第二轮谈判公共部门利益分配权重最大值，并与式（28）进行比较：

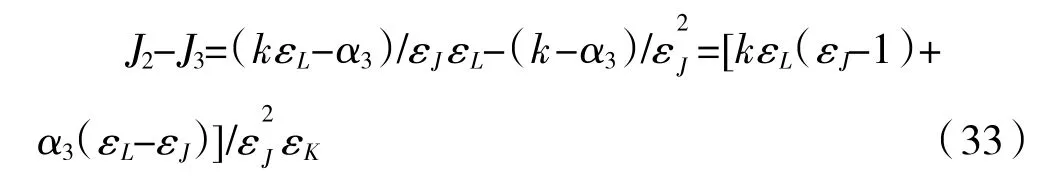
因为，1＜εJ＜εL，所以J2＞J3，故双方都不会选择进入第三轮谈判。

同理，在第一轮谈判中，本土产业同样要考虑要保证在第一轮谈判中公共部门权重大于等于其在第二轮谈判中公共部门权重，同时争取利益最大化，则：

把式（24）、式（32）代入式（34），整理得：

同理，此博弈模型为无限回合讨价还价模型，即表示其讨价还价的最大权重均为一致的，不论将关注点放在第一回合抑或是第三回合之始。因此推出：

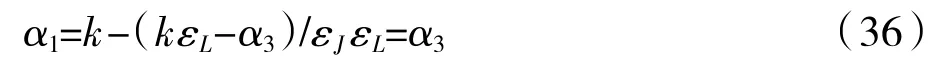
整理可得：

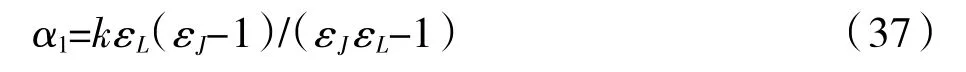
将式（37）代入式（24）、式（25）可以得出公共部门与本土产业的利益分配权重：

将k=（δK-1）/（δJ，LδK-1）代入式（38）、式（39）可得公共部门和本土产业利益分配的最终权重，并结合式（23）可得特色小镇PPP 项目三方主体利益分配权重均衡解：

分别用ΔωJ、ΔωK、ΔωL来表示此次博弈中产生利益分配权重差额，则：

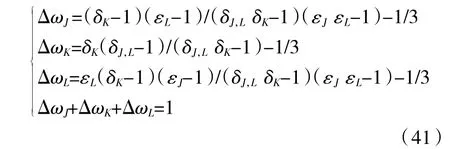
因此，可以计算出三方主体在此次博弈中的修正收益：

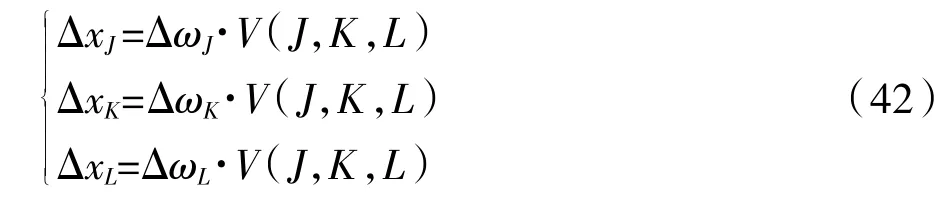
此时，对Shapley 值的利益分配模型进行修正：

整理得最终的特色小镇PPP 项目三方主体利益分配模型：

四、案例分析

湖南省M 镇是当地政府重点关注的特色小镇，为解决特色小镇发展资金问题，政府利用PPP 模式来引入社会资本发展特色小镇经济。该项目通过公开对外招标，确定由公共和私营部门共同联合本土产业承建。

经评估，该项目收益约85 亿元，若由公共部门、私营部门或本土产业独自承建，则收益分别为25 亿元、30 亿元和22 亿元。若公共部门与私营部门联合承建则收益为60 亿元，若公共部门和本土产业联合承建则收益为51 亿元，若私营部门和本土产业联合承建，则收益为57 亿元。项目谈判中的损耗系数分别为δJ，L=1.1，δK=1.27，εJ=1.2，εL=1.21，首先，通过式（5）、式（6）、式（7），得出讨价还价前（即修正前）的三方利益值；随后，三方通过讨价还价博弈实现对利益分配权重的修正，得到新的三方利益值。修正前后三方收益变化如表4 所示。

表4 三方主体利益分配表 单位：亿元

通过表4 可以清晰地看到，经过两轮讨价还价博弈之后，公共部门和私营部门分别向本土产业转移了1.4 亿元和1.1 亿元的利益，此时该项目三方主体获得利益均相比单独承建提高，同时由于对本土产业的激励，又基于原有利益分配基础上再次获得倾斜，本土产业更积极参加特色小镇建设和运营，推动项目顺利进展，促进项目成功。