期望交易量、信息交易量对收益率的影响研究——基于分位数回归模型

（上海理工大学 管理学院，上海 200093）

一、引言

收益率与成交量为股票市场中两个核心要素，包含了丰富的市场行为和市场信息。收益率与成交量的关系，即量价关系，通过反映股市的供需变化而帮助投资者判断市场或个股的运行趋势，成为了股票技术分析理论的基石。因此量价关系一直是本领域的热点，受到了国内外大量学者的关注。

关于股市量价关系的研究，主要集中在两方面：一方面是量价关系的影响机制，另一方面是量价关系的存在特征和运动规律。在影响机制方面，信息流理论占据主要地位。提出混合分布假说（MDH）的Clark（1973）[1]是这一理论的奠基人。Clark指出收益率和交易量是由共同的潜在信息流所决定，潜在信息流的出现会引起收益率和交易量的同步变动。Choi（2012）[2]将交易量作为信息到达的代理变量，发现交易量影响了市场间的信息流动，这一发现支持了混合分布假说的有效性；并认为交易量也可用于解释波动的不对称性，是用于预测收益率波动的有力工具。

在量价关系的存在特征和运行规律方面，学者们运用了不同的计量模型进行研究。夏天（2007）[3]使用条件自回归极差模型（CARR）研究了交易量和收益率的动态关系，发现混合分布假说适用于CARR模型。金春雨和郭沛（2010）[4]采用向量自回归模型研究了上证综指的交易量变动与收益率的关系，指出量价关系是非对称的。易文德（2010）[5]通过构建Copula 模型分别研究了上证综指、恒生指数和道琼斯工业指数的交易量与收益率之间的相依结构和相依程度，发现交易量与收益率之间存在上尾高下尾低的非对称相依关系。黄稚渊等（2018）[6]对股票高频数据建立了价格强度模型，发现交易量对其价格起助涨助跌的推动作用，且助涨效应较助跌效应更强。另外，黄稚渊等（2018）[6]指出交易量相比纯价格数据含有价格的额外信息。为了充分利用收益率的分布特征，分析不同分位水平下收益率与交易量的关系，林德钦（2014）[7]对上证指数建立了分位数回归模型，而任燕燕和李劭珉（2017）[8]对沪深300指数建立了基于工具变量的分位数回归模型，均表明收益率处于较低水平时，与成交量负相关，而收益率处于较高水平时，与成交量正相关。

交易量可以进一步分解成期望交易量和信息交易量，其中期望交易量代表了市场流动性，而信息交易量具有信息传递的作用。因此也有学者关注期望交易量和信息交易量对股票价格的影响。陈怡玲和宋逢明（2000）[9]指出我国股票市场中信息交易量比期望交易量能更好地解释股价波动。殷劼（2010）[10]研究上证指数发现期望交易量与预期收益率呈正相关，而信息交易量与非预期收益率呈负相关。但少有文献在收益率不同分位水平下，从期望交易量和信息交易量的角度分析量价关系。因此，本文将对交易量、期望交易量、信息交易量与股票指数收益率分别建立分位数回归模型，对比分析不同分位水平下的量价关系。

本文结构安排如下：第一部分，介绍相关理论和文献；第二部分，注明所用变量和模型；第三部分，实证分析，比较分析交易量变化率、期望交易量变化率和信息交易量变化率对收益率的影响；第四部分，总结与展望。

二、模型设定与变量选择

（一）分位数回归

分位数回归模型最早由Koenker 和Bassett（1978）[11]提出，主要用于研究金融变量间的相关关系，用因变量的条件分位数对自变量进行回归，用回归所得系数来表示自变量在各个分位点上对因变量的影响程度。与最小二乘法下的最小化残差平方和不同，分位数回归系数估计依据是最小化残差和，这既保留了非对称形式的特征又重新定义了最小化问题。相比于最小二乘法，分位数回归模型能提高数据利用率和参数估计精度，并全面分析在各个分位点的结果。

假定因变量是随机变量Y，自变量是K×1 维的随机变量X，{X1，X2，…，Xn}是X 的n 个样本观测值，对于任意τϵ（0，1），一般线性分位数回归模型为：

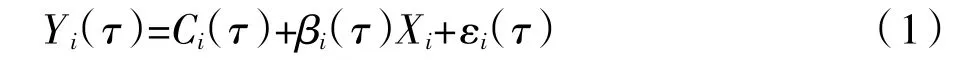
模型假设了在τ 分位条件下的残差项的值为0，即εi（τ）=0。回归系数βi（τ）表示了τ 分位条件下因变量Yi受自变量Xi的影响，亦表示了两变量间的相依性大小。

进一步估计系数的值：

其中，令u=yi（τ）-ci（τ）-βi（τ）xi，ρτ（u）=ρτ（yi（τ）-ci（τ）-βi（τ）xi），则有损失函数：

其中I（·）为一个示性函数。

（二）样本选取

不同股票指数包含的成分股不同，市值规模不同，这使各股票指数在投资者关注度、信息披露质量和避险功能等方面存在一定差异，而产生量价关系上的差异。因此，为全面考察A 股市场指数交易量对指数收益率的影响，本文选取了代表四种不同市值规模的样本指数：上证50、沪深300、中证500和中小300 指数，以分别表示A 股大中小盘的市场情况。样本区间为2010 年11 月1 日至2019 年11月1 日，共2 191 个交易日。

（三）变量说明

1.被解释变量。本文的被解释变量为股指的日对数收益率，即rt=lnpt-lnpt-1。

2.解释变量。本文的解释变量首先为日交易量。由于所选指数的日交易量对数序列是非平稳的，一阶差分后平稳，故本文参照易文德（2010）[5]，研究股指日交易量的对数变化率对其对数收益率的影响，以日交易量对数变化率作为交易量的代理变量，具体为vt=lnqt-lnqt-1。

另外，Li 和Wu（2006）[12]，郦金梁等（2012）[13]和文凤华等（2013）[14]指出交易量可分解为两部分进行分析：一部分是可预期部分，构成市场买进卖出的流动性指标，以衡量市场活跃度，称为期望交易量；另一部分是非预期部分，与价值信息相关的信息交易量。为全面分析交易量对收益率的影响，本文将交易量进一步分解为期望交易量和信息交易量两部分。

由于交易量对数变化率的高度自相关，参考Amihud（2002）[15]的一阶自回归方法，本文将交易量变化率分解成期望交易量变化率和信息交易量变化率：

其中，c 和bi是常数，εt是残差项。本文将残差项εt的估计值定义为信息交易量变化率，用表示；回归项[c+biυt-1]的估计值定义为期望交易量变化率，用表示。

由于υt对于rt不可实时得到，故本文在分位数回归模型中分别使用的是滞后一阶的日交易量的对数变化率（υt-1）、期望交易量变化率（）、信息交易量变化率（）。

3.控制变量。参考何平等（2014）[16]和杨杰瑞（2019）[17]的取法，考虑自变量交易量对数变化率的自相关性，本文选取滞后两阶的交易量对数变化率（υt-2）为控制变量。

（四）数据描述与检验

表1 为四指数日收益率和日交易量变化率的统计特征表。从中可知：交易量变化率的最大值、最小值的绝对值、方差均显著大于收益率，表明交易量的波动较价格更活跃。收益率的中位数均大于0且大于均值，偏度均小于0，峰度均大于3，表明收益率序列分布左偏、尖峰肥尾；交易量变化率的中位数均小于均值且小于0，偏度均大于0，表明交易量变化率序列分布右偏。JB 检验和ADF 检验结果表明四指数的收益率序列和交易量变化率序列均是平稳序列，不产生伪回归现象。另外，交易量变化率序列的峰度随指数成分股市值的增大而减小，而收益率序列的峰度随市值的增大而增大，表明量价关系与指数的市值规模存在关系。

表1 四指数收益率和交易量变化率的描述性统计

表2 给出了期望交易量变化率和信息交易量变化率的均值和方差。我们发现四指数的交易量变化率均值与其期望交易量变化率均值相近，且远大于信息交易量变化率，即交易量变化率均值主要由期望交易量变化率的均值表示。关于方差，表2 反映了交易量变化率方差与信息交易量变化率方差相近，且远大于期望交易量变化率方差，表明交易量变化率方差主要由信息交易量变化率的方差贡献。这与信息流量价理论一致，说明交易量是信息传递的重要介质，国内易文德（2010）[5]、文凤华等（2013）[14]亦证明了这一发现。

表2 期望交易量变化率和信息交易量变化率

三、实证结果分析

（一）交易量对指数收益率的影响

对上证50、沪深300、中证500 和中小300 指数的收益率和交易量变化率分别进行分位数回归，所得参数估计结果如表3 所示。从表3 可知，线性回归系数均不显著，且分位数回归系数的显著性优于线性回归，其中分位数回归系数在0.1 和0.25 分位点上显著性最强，而在高收益区间和极端低收益区间的显著性减弱，说明分位数回归所得的量价关系在不同分位区间不同。另外，低分位点的回归系数普遍大于0，高分位点的回归系数普遍小于0，表明量价关系的非对称性，即交易量上升对低收益率起促进作用，对高收益率起抑制作用，抑跌抑涨，存在“反向杠杆效应”，反应了A 股市场具有较强的投机性，这与Yeh 和Lee（2000）[18]、刘庆富和周程远（2012）[19]的研究结果一致。

表3 收益率与交易量变化率分位数回归的参数估计

对比不同指数，中证500 指数回归系数的绝对值一直大于沪深300 指数，且中小300 指数回归系数的绝对值一直大于上证50 指数，表明中小盘交易量变化率对收益率的影响更大，反映了中小盘股公司由于其经营情况和股价变动的较低资金成本被普遍认为稳定性更弱，故存在较多投机行为，易受信息刺激。另外，除了0.95 分位点，中证500 指数回归系数的绝对值也都大于中小300 指数；与此不同的是，上证50 指数回归系数的绝对值在高收益率区间大于沪深300 指数，而在低收益率区间均小于沪深300 指数，表明上证50 指数在高收益率区间量价关系更大，在低收益率区间量价关系更小。

（二）期望交易量与信息交易量对指数收益率的影响

郦金梁等（2012）[13]指出信息交易量促进了交易波动，而期望交易量体现了市场流动性。为了区分期望交易量和信息交易量对收益率的不同影响，本文分别建立了四个指数收益率与期望交易量和信息交易量的分位数回归模型，回归结果如表4、表5 所示。

表4 信息交易量分位数回归的参数估计

对比表3 和表4，我们发现，信息交易量变化率对收益率的系数与交易量变化率的系数在数值、符号及显著性上基本一致，这表明交易量对价格变化的影响主要来源于信息传递。在四种指数中，中证500 指数的信息交易量变化率回归系数最大且显著性最强，上证50 指数的信息交易量变化率回归系数最小且显著性最弱，这表明中小盘股的收益率对信息的敏感性较大盘股更强。

表5 期望交易量分位数回归的参数估计

由表3～表5 可知，期望交易量变化率回归系数的显著性较交易量变化率和信息交易量变化率有了明显提高。并且在收益率不同分位水平下，期望交易量变化率系数符号的差异变得不明显，量价关系的非对称性弱化，期望交易量变化率对收益率的影响方向除极端情况外近似一致。这表明期望交易量作为体现市场流动性的指标，与收益率的关系是稳定的，对收益率起着促进作用。而相比于高分位点，低分位点处的期望交易量变化率回归系数绝对值更大，说明期望交易量变化率对低收益率区间影响更大，对高收益率区间影响更小，即下降市场环境对交易流动性更敏感。

另外，表5 显示上证50、沪深300、中证500 的回归系数依次增大，表明中小盘股票收益率对期望交易量变化率的敏感性较大盘股更强，对流动性更敏感，这是由于大盘股公司的经营稳定性、信息透明度和行业竞争力受到更多投资者的认可，其股票的流动性和流动性的稳定性均优于中小盘股，使之在上涨市场环境获得更多的交易量而在下跌市场环境失去更少的交易量。

四、总结与展望

本文选取上证50、沪深300、中证500 和中小300 指数在2010 年11 月至2019 年11 月间的日收益率和交易量变化率数据，通过分位数回归模型分析前一天的交易量变化率对当天收益率的影响，并与期望交易量变化率和信息交易量变化率的结果进行比较分析，结果表明：

第一，信息交易量是交易量影响股价的主要途径；而期望交易量提供了交易和价格变化的流动性，对股票指数日收益率的影响显著且稳定。

第二，股价波动的杠杆效应仅限于信息交易量的影响，即信息交易量对低收益率起促进作用，对高收益率起抑制作用，而期望交易量对收益率的影响基本上是正相关的。

第三，下降市场环境中的收益率对交易流动性的敏感性较上升市场环境更强，并且中小盘股票收益率对信息和流动性的敏感性较大盘股更强。

基于上述交易量变化率、信息交易量变化率和期望交易量变化率对收益率影响的研究结论，本文提出以下建议：

第一，加大金融创新力度和金融市场开放程度。通过沪伦通、纳入MSCI 等金融开放措施，提高外资金融机构在华业务的积极性。另外，也可推出更多的金融衍生品，在丰富我国金融产品的同时，提高金融市场的流动性。

第二，进一步提高上市公司质量，加强上市公司的信息披露。一方面，对上市公司严格监管，规范上市公司行为。完善退市机制并严格执行，严格剔除不符合要求的公司，促使上市公司提高自身的经营能力。另一方面，明确上市公司信息披露制度和原则，制定相关法规，督促上市公司按时披露信息，并保证所披露信息的真实性。通过这两方面的措施，可以减少金融市场的波动，降低市场风险。