基于竞争机制粒子优化算法选择NIDS系统特征子集*

周利均

（中国电子科技网络信息安全有限公司，四川 成都 610041）

0 引言

入侵检测系统是计算机系统的关键组成部分，一般分为外部异常检测和内部误用检测，近年已有相关的系统研究和综合性论述[1-5]。异常检测核心是通过训练数据搭建分类模型来实时分析检测网络入侵行为，重点是检测的实时性、准确性以及兼容性等。网络入侵检测系统通过分析TCP/IP数据流来挖掘分析潜在的异常攻击行为，在万物互联的网络时代显得尤为重要。攻击者攻击手段已经向着自动化、智能化方向发展[6-7]。面对攻击手段更加隐蔽、攻击方式更加多样的情况，本文研究在构建NIDS系统分类器模型中的特征优化选择问题，以便适应海量网络流量数据的挖掘分析。

构建NIDS系统分类器核心是选择较为合适的特征子集[8-14]，具有D个特征的流量数据，会有2D-1种不同的特征子集组合。合适的特征子集既可以消除冗余信息，也可以降低计算的复杂度[15]。根据评价方式，特征选择主要分为3种[16]。

（1）过滤式（Filter）：先选择特征再训练分类器，主要有卡方检验、信息增益以及相关系数法等。

（2）包裹式（Wrapper）：分类器作为分类评价函数选择最优子集，主要有GA、PSO、DE以及ABC等算法。

（3）嵌入式（Embedding）：特征选择与分类器学习融合，主要有正则化方法等。

以上3种方式比较，Wrapper方法具有更好的分类性能[17]，因此启发式优化算法在该领域有广泛应用。GA算法通过生产染色体种群解，通过每一代的选择、交叉和突变完成进化，已有相关特征选择研究[18-19]，在大数据等特征选择领域也有相关研究[20-23]。人工蜂群算法通过初始化蜂群，采用不同角色之间的信息交流、转换以及协作来实现优化，该算法也在特征选择有相关研究[24-25]。以上方法的参数设置对优化结果有较大影响。

粒子群优化算法通过初始化粒子种群，每个粒子在搜索空间中独立搜索其局部最优解，速度代表向最优解靠近的快慢，用位置代表移动方向，通过记忆局部最优并采取全局共享机制获取全局最优解，所有粒子根据其局部最优和当前全局最优更新其位置和速度。PSO算法用于特征选择问题已有相关研究[26-29]，但是PSO因其采用的经验学习机制，存储的个体最优极易使得算法陷入局部最优解，且针对海量数据时会消耗大量的计算资源。

基于PSO算法的思想，提出了一种基于竞争机制的粒子优化算法。该算法随机选取粒子对竞争，竞争中的优胜者直接进入下一代，失败者向优胜者学习。学习机制舍弃了对局部最优和当前全局最优解的依赖，因此相对PSO算法不易陷入局部最优解，且每次迭代只有一半的粒子向优胜粒子学习，因此在解决大规模数据优化方面更具有优势。本文以KDDCUP99的训练集（10%）和测试集[30]来对算法进行验证，利用错误率和选择特征数的线性组合为适应度函数，准确率更重要，权重值设置更大，错误率来源于分类结果，采用KNN等分类算法计算。

本文共分为5个部分：第1部分为序言，主要回顾该方向前期研究成果以及本文研究思路；第2部分主要介绍竞争机制粒子优化算法原理，并对算法模型进行稳定性分析，求得控制参数取值范围，再分析了二值化方法的更新函数及流程；第3部分主要分析KDDCUP99数据集，并研究该数据集的预处理方法及流程；第4部分是实验设计及验证，利用提出的优化算法选择合适的特征子集，利用选择的特征子集搭建训练模型，采用交叉验证方法的训练模型的检测准确度进行验证；第5部分是结论，根据本文提出的算法模型仿真得出的实验结果得出结论，结合该方向分析和展望后续研究重点。

1 竞争机制粒子优化算法

1.1 竞争机制粒子优化算法描述

竞争机制粒子群优化算法框架见图1，其中P(t)和P(t+1)分别代表第t和t+1代粒子群，每一代粒子群共有m个粒子，每个粒子位置和速度为n维，第i个粒子位置和速度分别表示为：

在每一次迭代过程中，粒子群P(t)被随机分成种群大小为m/2的两部分（若m为奇数，随机划分时竞争优胜者比失败者多1个粒子，从优胜者子群里随机选取1个补充到失败者子群），从两个子群中分别选择粒子成对竞争，优胜者直接进入下一次迭代，失败者通过学习机制向优胜者学习更新，再进入下一代，即每一次迭代每个粒子只参与1次竞争，只有m/2的粒子通过学习机制更新。可见，该算法计算消耗主要是在失败粒子的更新上，计算复杂度为O(mn)。

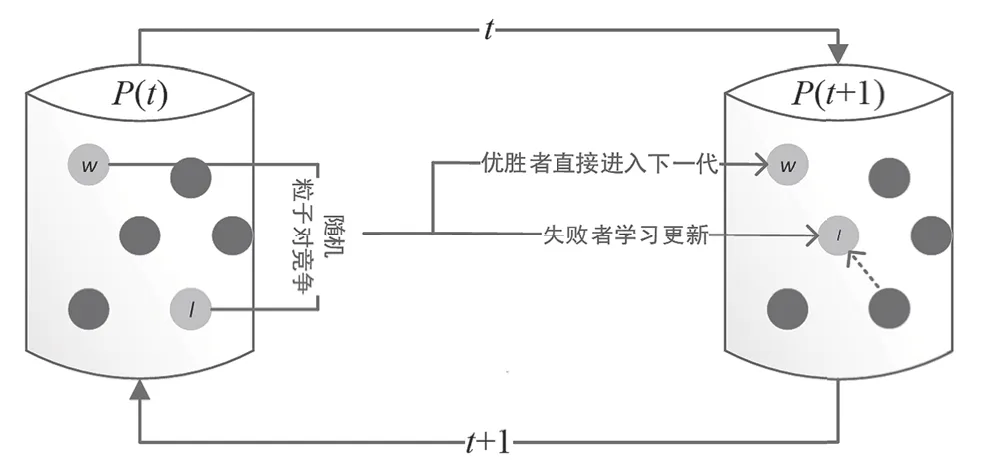
图1 竞争机制粒子优化算法框架

令Xl,k(t)和Vl,k(t)表示第t次迭代中第k轮竞争中失败粒子的位置和速度；Xw,k(t)和Vw,k(t)表示第t次迭代中第k轮竞争中优胜粒子的位置和速度；R1(k,t),R2(k,t),R3(k,t)∈[0,1]n表示第t次迭代中，第k轮竞争中失败者向优胜者学习的随机数向量，其中k=1,2,3,…,m/2。

1.2 算法稳定性分析

根据式（3）和式（4），改写得到动态方程形式：

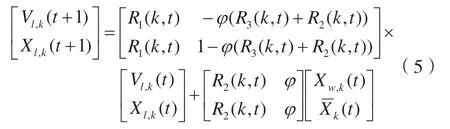
改写成如式（6）所示的形式，成一对一对应关系：

其中，A为状态转移矩阵，B为输入矩阵。

根据劳斯稳定性判据[31]，上述动态方程稳定的充分必要条件是：劳斯表中第1列各值为正，如果劳斯表第1列中出现小于零的数值，系统不稳定，且第1列各系数符号的改变次数，代表特征方程（7）的正实部根的数目。

列出特征方程（7）的劳斯表，如表1所示。

表1 特征方程劳斯表

根据稳定的充分必要条件，第1列各值为正，R1(k,t)介于[0,1]之间是正数，只需满足φ(R3(k,t)+R2(k,t))-R1(k,t)-1＞0，求得：

由于R1(k,t),R2(k,t),R3(k,t)∈[0,1]n，显然不等式（8）右侧取得最小值时，分母趋近于2，分子趋近于1，因此其最小值趋近于0.5，即φ＞0.5。此时，上述动态系统是稳定的，可以实现解空间内的快速收敛。

1.3 二值化方法

竞争机制粒子优化算法每次迭代时更新粒子速度，对粒子速度利用S函数[32]进行二值化处理，并根据规则对粒子位置进行0、1的离散空间处理，其中1代表选择该特征，0代表不选择该特征。

3种S函数表达式、S函数图形、粒子位置离散化公式详见表2。

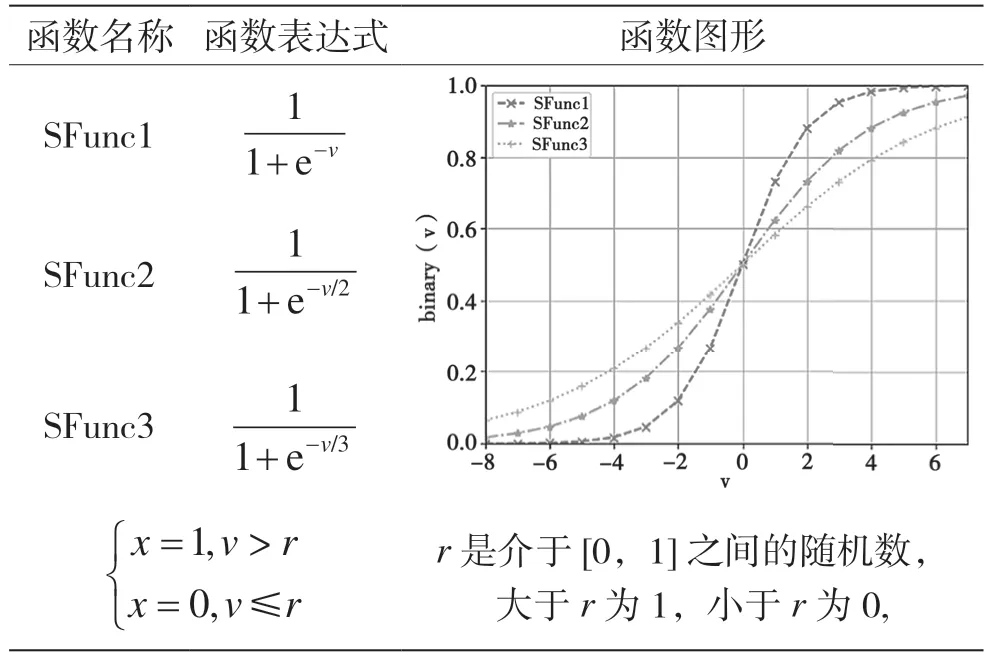
表2 S函数表达式及图形

连续空间到离散空间的映射关系详见图2。

2 KDDCUP99数据集预处理

2.1 KDDCUP99数据集分析

从源IP地址到目标IP地址，通过TCP或UDP协议建立连接，每个网络连接分为正常或异常。异常类型共分为4大类共39种攻击类型，其中22种攻击类型在训练集中，另外17种攻击类型在测试集中。4种异常类型分类如下。

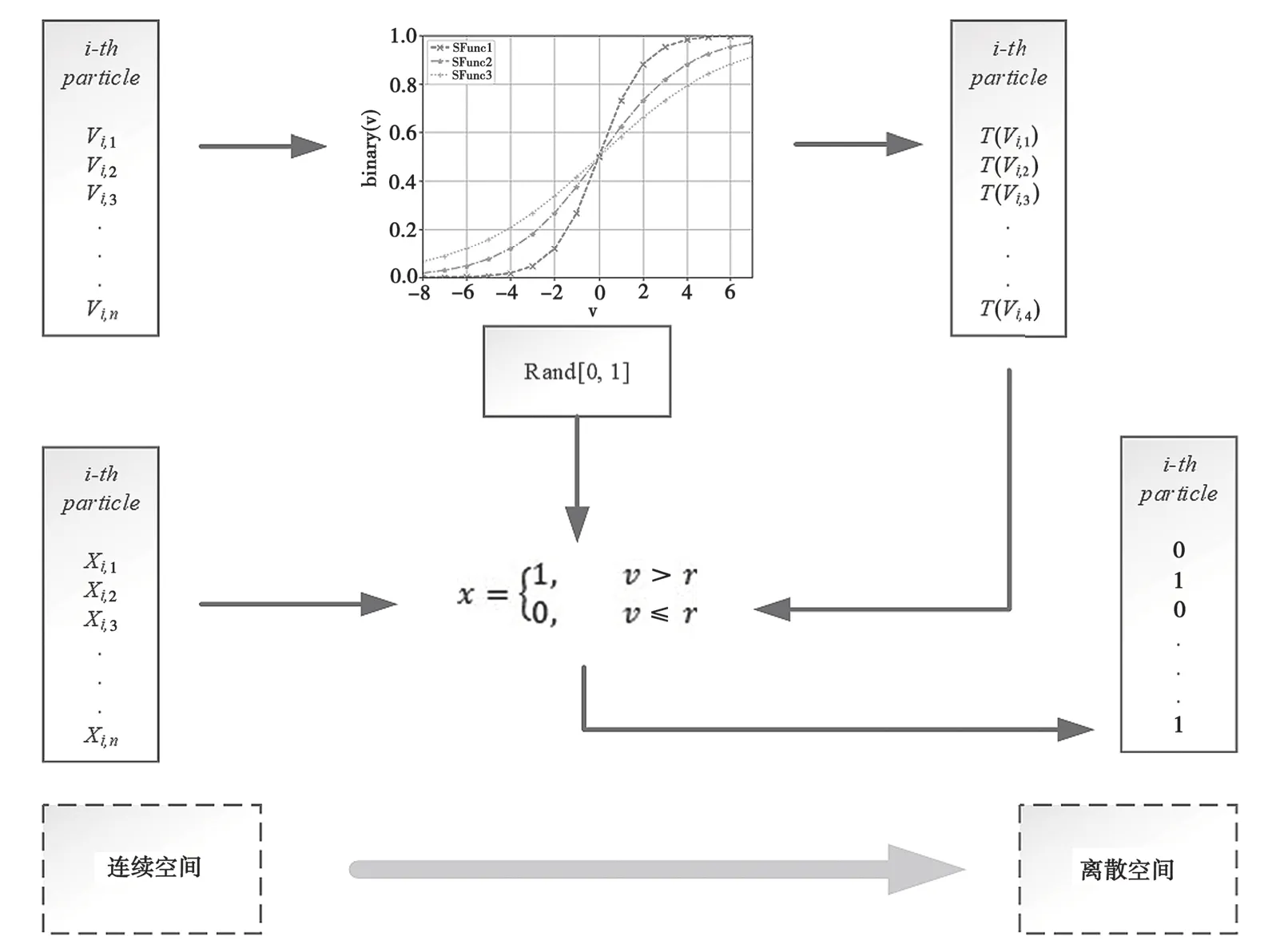
图2 连续空间到离散空间映射关系

（1）Denial of Service Attacks（DoS）：拒 绝服务攻击，有back、land、neptune、pod、smurf和teardrop共6种。

（2）User to Root Attacks（U2R）：来自远程主机的未授权访问，有ipsweep、nmap、portsweep和satan共4种；

（3）Remote to Local attacks（R2L）：未授权的本地超级用户特权访问，有ftp_write、guess_passwd、imap、multihop、phf、spy、warezclient和warezmaster共8种。

（4）Probing attacks：端口监视或扫描，以躲避系统安全控制获取信息，有buffer_overflow、loadmodule、perl和rootkit共4种。

KDDCUP99每一条连接记录由41个特征组成，分为4种类型（基本特征，内容特征，内容特征，流量特征），第42位是特征标签，特征数据结构见图3。KDDCUP99由约500万条记录组成，同时还包括10%的训练子集和测试子集，样本类别分布如图3所示。部分特征属于字符型，在数据预处理时需要转换成数值型；部分连续性数据需进行数据标准化处理，避免出现数据覆盖现象。

图3 特征数据结构

2.2 字符型转换成数值型

图3为KDDCUP99数据集特征数据的数据结构，斜体下划线标注的是字符型特征，根据其在列表中出现的顺序值进行数值替换。以protocol-type为例，有3种协议类型，依次为tcp、udp和icmp，根据上述原则一次将其替换成0，1，2。同样，service共有70种网络服务类型，转换成数值0～69；flag共有11种网络连接状态，转换成数值0～10；label共有22种攻击类型，外加正常状态标识normal（放在攻击类型之前），转换成数值0～22。

以上将KDDCUP99数据集中字符型转换成了数值型，便于后续进一步进行数据处理。

2.3 数据标准化

KDDCUP99数据集中特征数据较为分散，特征数据的数值类型有连续型和离散型，连续型特征数据之间的数值差也较大。为了避免数值差异较大导致的数据覆盖现象，提高模型训练速度，需对数据进行标准化处理。本文采用极值法，即带正向指标的极差变换法。通过式（9）处理后，数据被标准化至[0，1]区间。

3 实验设计及验证

3.1 适应度函数

本文适应度函数采用分类错误率与特征数的线性组合，通过调整权重系数α的值分配分类错误率和特征数影响比重：

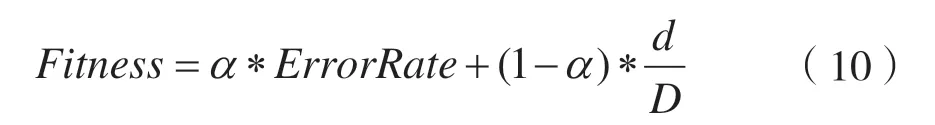
ErrorRate代表分率错误率，由python自带KNN分类器计算；d代表第i个粒子所选取的特征数；D是每个粒子总的特征数，针对KDDCUP99数据集，D为41；α为权重值，用于调节错误率和选择特征数权重。

3.2 参数设置

经过数据预处理的KDDCUP99数据集共有494 021条数据，利用train_test_split函数将该数据集随机分成训练集和测试集。在进行模型训练和预测中，为了便于快速计算，随机从训练集和测试集中各选取1 000条数据，数据标签选取相对应的标签。

用预测精度、最优适应度值、最差适应度值、平均适应度值以及选择特征来评估模型预测结果。

参数设置如表4所示。

表4 参数设置

3.3 实验结果

3个S函数所对应的预测精度、最优适应度值、最差适应度值以及平均适应度值如表5所示。

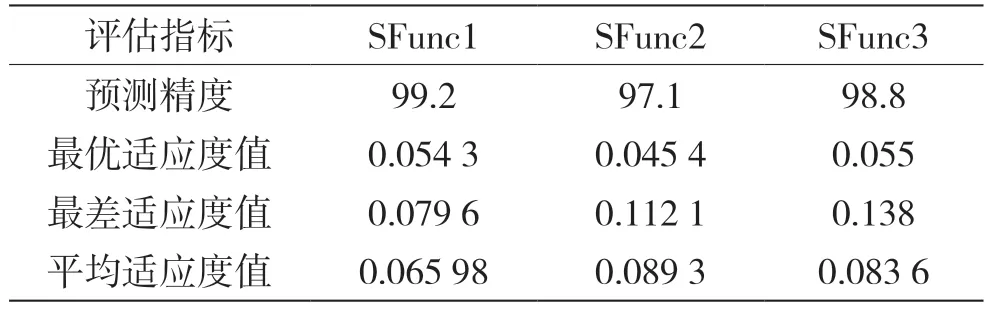
表5 预测精度及适应度值

3个S函数所对应的选择特征数个数及位置如表6所示，在每条记录41个特征中，0表示不选择，1表示选择。

表6 特征数个数及位置

适应度值变化曲线详见图4。可以看出，初始化适应度值在迭代之处能到达一个较为理想的水平，且SFunc1较另外两个转换函数较为平整，SFunc2和SFunc3均有较大突变，突变后趋于稳定。可以看出，基于竞争机制的二值化粒子优化算法具有在短时间内可以到达较为稳定的状况。

以SFunc1为例，设置K值范围为1～20，采用sklearn的cross_val_score进行交叉验证，求取准确度的平均值。通过比较准确度值，选取最合适的K值，实现参数调优。通过仿真计算，准确度随K值变化曲线详见图5，其中K=4时准确度为0.994 5，此时为模型参数最优。

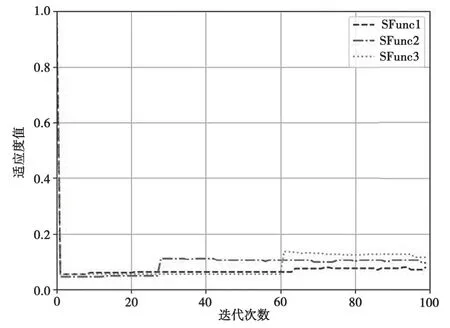
图4 适应度值变化曲线

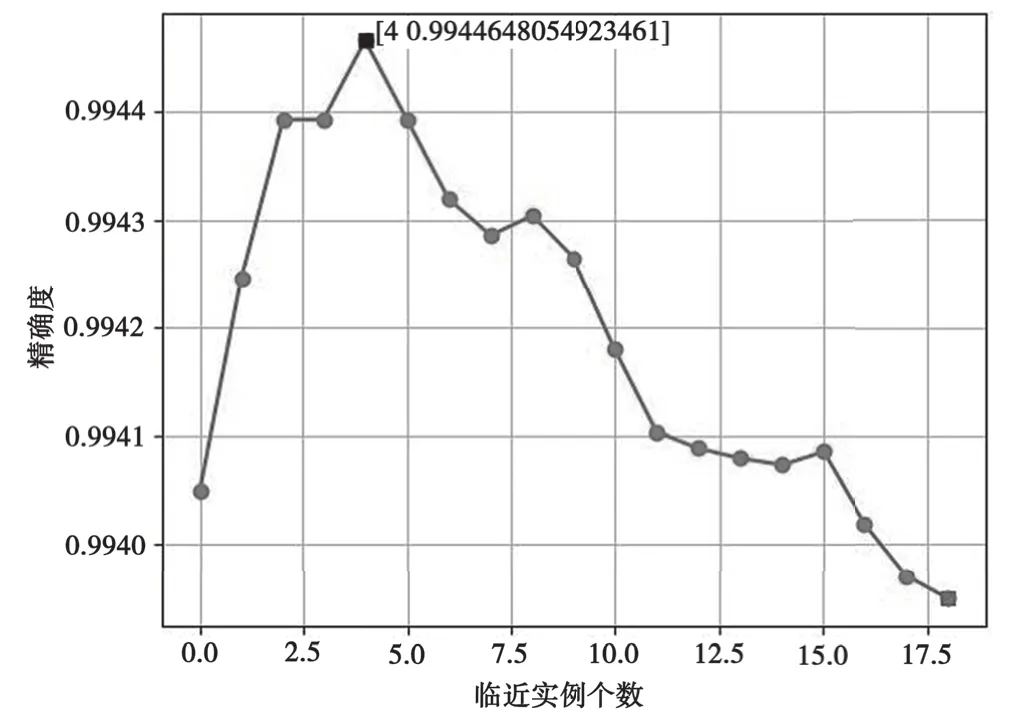
图5 精确度随K（实例个数）值变化曲线

4 结语

本文采用二值化竞争机制粒子优化算法优化选择KDDCUP99数据集的特征子集，实现数据的降维处理，创新性地采用稳定性理论分析算法模型，选取调控参数取值范围，分析了KDDCUP99数据集的预处理思路、方法和流程，并采用sklearn的KNN算法搭建训练模型，利用选择的特征子集进行模型训练，利用交叉验证机制对模型进行精确度校验。实验结果表明，通过优化算法选取的特征子集搭建的训练模型具有较高的精确度，且在处理大数据时具有较大优势。

本文以KDDCUP99数据集进行验证。KDDCUP99数据集主要是网络流量数据，在入侵检测领域具有较高的代表性。后续将以实际入侵检测模型搭建需求为牵引，将本文研究的优化算法结合实际需求搭建合适的入侵检测模型，对实际的入侵检测行为进行实时的分析感知。