考虑滑带土蠕变特性的边坡长期稳定性分析

2020-08-14古鹏翔骆俊晖刘先林

安全与环境工程 2020年4期

古鹏翔，骆俊晖，刘先林，马冲

(1.广西阳鹿高速公路有限公司，广西南宁 530021；2.广西交通设计集团有限公司，广西南宁 530029;3.中国地质大学数学与物理学院，湖北武汉 430074)

随着我国经济建设的不断发展，各类基础设施正在逐步完善，交通运输业也得到了长足的发展，如各类公路的修建、铁路运行速度的不断提升等，都给人们的日常生活带来了诸多便利[1]。道路是一种条带状的构筑物，需要跨越众多地质条件复杂的区域，其正常使用期间的安全运营与众多因素密切相关[2]。边坡是道路建设中经常遇到的工程状况之一，其稳定性与邻近构筑物和人类工程建设活动密切相关。现有的研究表明，边坡的失稳大多发生在软弱夹层处，该处岩土体的工程性质较差，常表现为强度低、渗透性强、细粒含量高和矿物成分复杂多样等特点[3-5]。滑带土是此类岩土体的典型代表之一。

滑带土是指在滑坡的发生和发展过程中形成的强度较低，呈可塑状、软塑状甚至流塑状的岩土体。蠕变特性是滑带土具有的典型特征之一，在一定的应力状态下，滑带土的变形随时间的推移不断增加，累积变形至一定程度后，成为诱发滑坡的重要因素[6]。已有学者对滑坡滑带土的蠕变特性进行了广泛的研究，主要通过室内试验研究了滑带土长期强度、蠕变曲线特征以及地质条件与外部自然环境对滑带土蠕变特性的影响等[7-10]。这些前人研究结果明确了滑坡滑带土应力-应变特征的时效性及其对边坡长期稳定性的重要性。为了揭示滑坡滑带土蠕变特性的原因，一些学者研究了不同含水量、颗粒粒径和矿物侵蚀程度等条件下滑带土蠕变特征的差异，并据此建立了许多理论、半理论模型来描述滑带土蠕变特性的影响因素与其力学特性之间的相互关系[11-14]。虽然人们已经认识到滑带土的蠕变特性对边坡安全稳定的重要性，但是在对边坡的长期稳定性进行评价时，鲜有考虑滑带土蠕变特性的影响[16]，同时考虑滑带土蠕变特性的边坡长期稳定性预测分析也少有相关报道。

鉴于此，本文以某岩质边坡为工程实例，首先在已有滑坡事故调查的基础上，明确了边坡软弱夹层中滑带土的蠕变特性对边坡长期稳定性的重要性，并通过现场监测和室内环剪试验，探明不同含水量和法向应力条件下边坡滑带土的蠕变变形曲线特征；然后通过引入有关损伤变量的经验关系式，建立用于描述边坡滑带土蠕变特性的非线性蠕变本构模型；最后将模型计算结果与实测结果进行对比，验证所建立模型的有效性和可靠性，并通过预测边坡软弱夹层塑性剪切应变的发展趋势，对边坡的长期稳定性做出了评价，讨论计算模型对于外部环境因素影响的局限性。该研究结果对于边坡长期稳定性的正确评价以及滑坡灾害的高效预警具有重要的借鉴与参考价值。

1 工程概况

某岩质边坡整体地势呈东南高、西北低，边坡纵、横向长度约为300～400 m，海拔高程范围为900～1 400 m。该边坡坡向为290°，坡角为60°～65°，岩层产状为290°～320°∠11°～13°，边坡上潜在滑体(变形体)厚度约为10～60 m，判断为一大型顺层岩质滑坡。据现有调查资料发现，该边坡在2011年4月底发生中型滑坡，滑坡整体横向宽度约为250 m，纵向长度约为200 m，崩塌体积约为20万m3(见图1)。通过对此次滑坡事故的调查研究发现，该滑坡体滑面是一软弱夹层，岩层的倾角较缓，在15°以内。若按照传统极限平衡理论对该滑坡潜在滑动体的稳定性进行评价，则其处于安全范围内，这与现有事实相违背，故该滑坡发生的根本原因有待进一步探索。

图1 具有软弱夹层的某岩质边坡发生滑坡前后的照片Fig.1 Photos of a rock slope with soft interlayer before and after the landslide

为了防范此类滑坡事故的再次发生，工程建设人员加强了对该边坡现有危岩体的变形监测，经过长达一年的现场监测，发现该边坡在海拔1 300 m左右处的人工平台处变形体处于蠕动变形阶段，其3个典型监测点(B5-1、B8-1、B10-1)的位移监测结果见图2。

图2 含缓倾软弱夹层高边坡的位移监测数据图Fig.2 Displacement monitoring data chart of high slope with gently-inclined soft interlayer

由图2可见，该边坡3个监测点的位移随着时间的推移均有不同程度的增长，变形曲线表现为波动式增长，其中最大位移增量达5 cm。与此同时，现场监测还发现，边坡中存在泥化夹层软弱带，当地雨季期间泥化夹层软弱带中存在水分渗出现象。该边坡泥化夹层软弱带中土体的含水量在15%～30%之间，土体的黏聚力和内摩擦角分别约为60 kPa和11°，边坡软弱夹层上下灰岩的黏聚力和内摩擦角分别约为37.54 MPa和32.52°。上述边坡变形监测与软弱夹层的调研结果表明，在自然降雨等因素的诱发下，高边坡变形体处于蠕动变形阶段，随着时间的不断推移，边坡软弱夹层强度不断丧失，其变形体将会沿着软弱夹层发生滑动、失稳。因此，研究边坡软弱夹层中滑带土的蠕变特性，对于评价边坡的长期稳定性至关重要。

2 边坡软弱夹层中滑带土的蠕变特性

本文通过室内环剪试验研究了边坡软弱夹层中滑带土的蠕变特性。

2.1 试验材料与方法

现场取某岩质边坡软弱夹层中的滑带土，密封后，尽量减少扰动并立即运输至室内实验室。为了研究滑带土的蠕变特性，对人工配置不同含水量的重塑滑带土试样进行环剪试验。重塑滑带土试样含水量w分别设置为15%、19%、23%、27%、31%，试样干密度控制为1.68 g/cm3，与原状土干密度一致。滑带土的天然含水量在18.75%～26.86%之间，为了使重塑滑带土试样制备的含水量与天然含水量一致，故将其含水量设置为15%～31%。根据边坡软弱夹层上覆岩土体厚度变化，设置环剪试验的法向应力σ为200 kPa和400 kPa。剪切试验开始前，需要对试样进行固结，分两段过程将法向固结压力加载至1 000 kPa，并维持6 h后，以设定速率将法向应力减小至需要水平(200 kPa和400 kPa)。由于固结阶段的法向应力高于剪切过程所需的法向应力，因此在法向应力逐渐减小的过程中，试样有可能会产生回弹变形。为了避免这一影响，各级法向应力均保持2 h后(法向变形稳定)再进行剪切试验[16]。

环剪试验中保证每一级剪切应力加载时间不小于5 h，每一级剪切应力加载最后2 h内试样位移量小于0.01 mm后，进行下一级剪切应力的加载。破坏级剪切应力加载到试样产生明显破坏时，停止试验。环剪试验过程中切向位移和剪切应力的数据采集频率为3 min/次，环剪试验具体加载方案见表1。

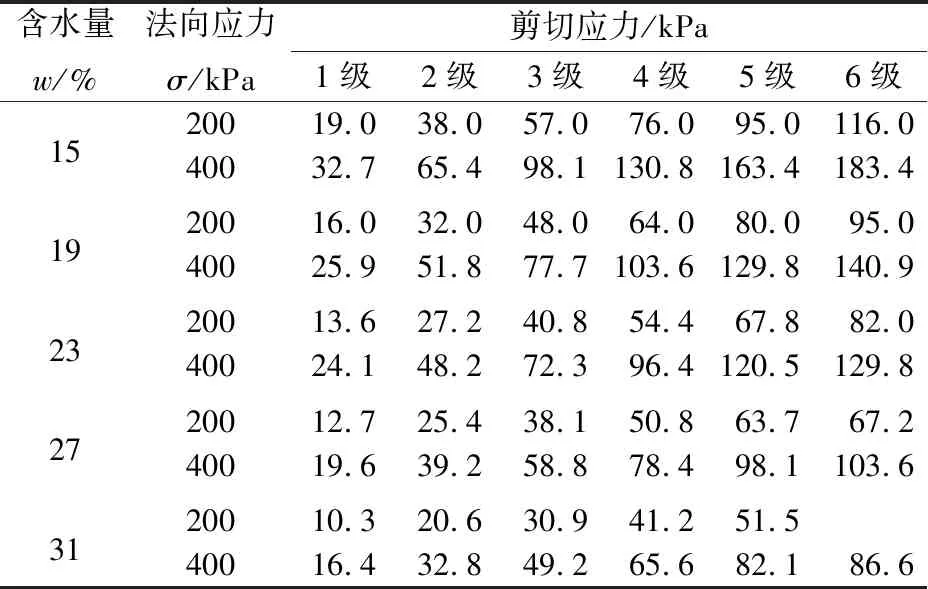
表1 环剪试验加载方案Table 1 Loading program of ring shear test

2.2 滑带土蠕变特性分析

岩土材料的蠕变特征是指，在保持应力不变的条件下，应变随时间推移而不断增长的现象。图3为不同法向应力条件下，具有不同含水量的滑带土蠕变变形曲线。

由图3可以看出：①所有滑带土试样的剪切曲线均具有蠕变特征，即各级剪切应力条件下，试样的剪切应变(Y-应变)随着时间(X-时间)的增长存在不同程度的增加；②含水量和法向应力对试样的蠕变特性存在影响，即相同法向应力条件下，含水量越大的试样，蠕变特征越明显，且400 kPa法向应力下相同试样的蠕变特征显著于200 kPa法向应力条件下的结果；③第6级剪切荷载作用下，试样经历了短暂的稳定蠕变变形后，蠕变变形产生了突变，蠕变变形急剧增大，试样发生了完全破坏；④虽然试样具有不同的含水量，但其在相同法向应力下发生破坏的时间相差不大(σ=200 kPa、w=19%的试样除外)。

值得注意的是，滑带土试样的蠕变变形曲线具有非线性蠕变变形特征，如σ=400 kPa时，第5级剪切荷载作用下滑带土试样的应变(Y)-时间(X)曲线[见图3(b)]。这是由于滑带土试样中含有较多的颗粒介质，在环剪应力条件下，颗粒会发生滑移、错动、翻爬等现象，这是产生非线性蠕变变形特征的主要原因；而含水量的差别，会导致滑带土试样中孔隙水压力、颗粒之间的相互接触状态发生改变，进而影响其在不同剪切应力状态下的蠕变变形特征。

图3 不同含水量和法向应力条件下边坡滑带土的蠕变变形曲线Fig.3 Curves of creep deformation of the sliding zone soils with different moisture content and normal stress

3 边坡长期稳定性计算与分析

3.1 边坡长期稳定性计算模型

根据某岩质边坡的潜在滑动面(软弱夹层)方位，本文选取该边坡两处典型工程地质剖面进行边坡长期稳定性计算与分析，见图4。该边坡两处典型剖面的人工微平台处均设置有一个位移监测点，即监测点A和B。本文利用ANSYS商业软件对边坡长期稳定性计算模型进行建模处理和网格划分，其中对该边坡的潜在滑动面区域网格进行了加密处理，以提高计算结果的精度。将前处理完成的计算模型，导入有限差分软件FLAC3D软件中，对边坡潜在滑动面的上覆岩土体采用传统Mohr-Coulomb准则、滑带土采用非线性损伤蠕变准则进行了应力、应变计算。

图4 某岩质边坡典型剖面工程地质剖面图Fig.4 Engineering geological profile of the typical sections of the rock slope

在前期剪切试验结果和现有损伤力学分析的基础上[3]，得到具有蠕变特征的滑带土瞬时弹性模量的损伤变量D1(w)和黏性系数的损伤变量D2(w)均与含水量w之间呈指数关系，其表达式如下：

(1)

式中:Z为土体物理量参数变量号，括号中15表示土体含水量为15%;a、b、c为无量纲系数。

图5为非线性黏弹塑性模型及各元件组合示意图。该模型由虎克弹簧、Abel黏壶和塑性体3种元件组成，其中E表示滑带土瞬时弹性模量(MPa)；μ1、μ2分别表示两个Abel黏壶的黏性系数(GPa/h)；β1、β2分别表示两个Abel黏壶的分阶阶数；σs为夹层土体的屈服应力(MPa)；ε1、ε2、ε3分别代表各串联部分的应变。

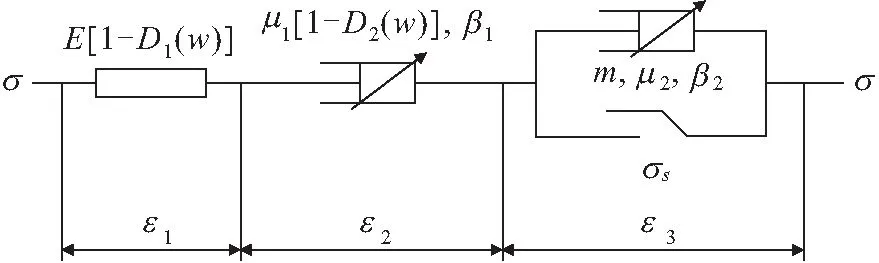
图5 非线性黏弹塑性模型及各元件组合示意图Fig.5 Schematic diagram of the non-linear iscoelastic plastic model and the combination of elements

当剪应力水平τ小于夹层土体的屈服应力σs时，土体的应力-应变关系为

(2)

当剪应力水平τ大于夹层土体的屈服应力σs时，土体的应力-应变关系为

(3)

将前述的滑带土黏性系数损伤变量D2(w)与含水量w的关系式[公式(1)]代入，得到滑带土的应力-应变关系模型如下：

(4)

式中:ε为应变；τ为切应力(MPa)；G为剪切模量(MPa)；t为时间(d)；Г为张量；β为分阶阶数；μ为黏性系数(GPa/h)。

模型中基本力学参数ε、τ和G可通过室内土工试验直接获得；β、μ和m参数可利用反演的方法获得，具体操作过程可参考文献[3]。

3.2 边坡长期稳定性计算结果与分析

根据室内环剪试验结果并结合参数反演的方法获取了某岩质边坡计算剖面土体的主要力学参数值，具体见表2。

表2 某岩质边坡计算剖面土体的主要力学参数值Table 2 Mechanical parameters of the soil in the calculated sections of the rock slope

图6为某岩质边坡计算剖面上监测点位移的模型计算结果与实测结果对比。

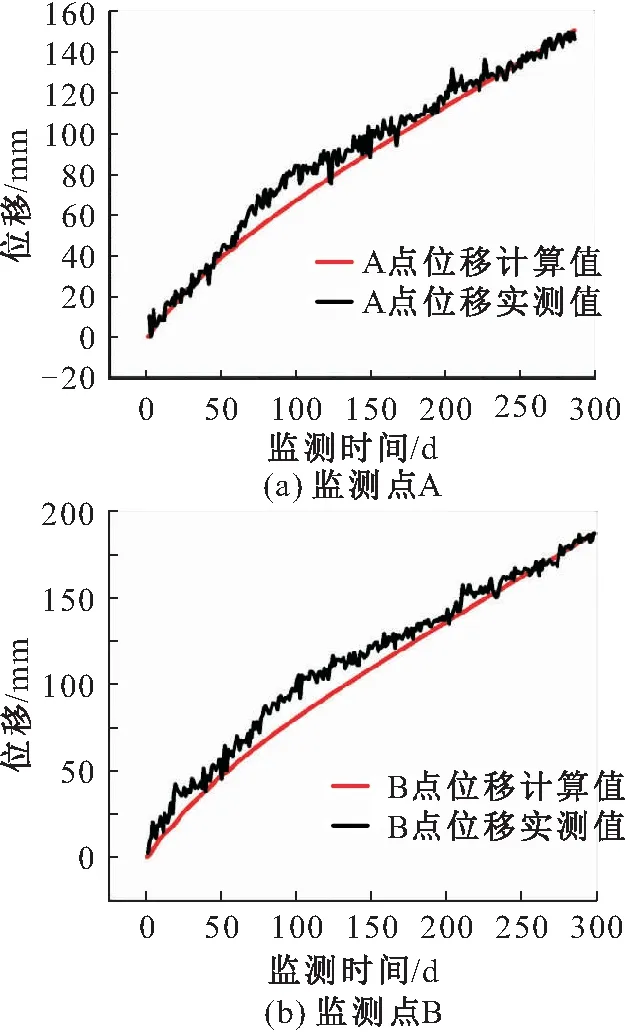
图6 某岩质边坡计算剖面上A和B监测点位移的模型计算结果与实测结果对比Fig.6 Comparison of displacement at the detection point A and B on the sections for calculation between the calculated results and the measured results

由图6可见，整体来说，边坡计算剖面上两处监测点A和B位移的模型计算结果与实测结果较为吻合，两者变化趋势基本一致，一年后的位移量相差无几。

由于降雨、气温等自然条件的复杂多变，监测点实测位移随监测时间的增长呈波动式增加，且实测值较计算值偏高，这是由于基于滑带土蠕变特征的模型计算并未考虑边坡所处自然环境的影响，然而降雨入渗、气温交替变化等均会对边坡的稳定性产生一定的不利影响。通过将该边坡计算剖面上两处监测点A和B位移的计算值与实测值的对比，结果表明考虑边坡滑带土蠕变特性的应力-应变计算模型能够合理地描述边坡潜在滑动面的长期变形特征，可用于边坡安全的长期评价与灾害预警。

3.3 边坡长期稳定性预测

图7为未来一年内某岩质边坡计算剖面两处监测点A和B位移的预测结果。

图7 未来一年内某岩质边坡计算剖面上A和B监测点位移的变化曲线Fig.7 Curves of displacement at the detection point A and B on the calculation sections in the rock slope in the next year

由图7可见，在现有地质条件下，一年后边坡计算剖面上监测点A的位移量约为200 mm，监测点B的位移量约为300 mm；位移量随时间的逐渐增加，其增长速率不断减小，符合滑带土蠕变变形的基本特征，即在应力状态基本不变的条件下，其变形随时间缓慢增加。当边坡软弱潜在滑动体的变形量积累到一定“量”时，就会发生“质”变，此时其变形量会在极短时间内急剧增加，导致边坡失稳破坏。

为了全面地评价该边坡的长期稳定性，本文对未来一年内边坡1-1′和2-2′剖面软弱潜在滑动面的塑性剪切变形及其发展趋势进行了模拟计算，其剪应变增量的变化云图见图8和图9。分别选取4个月、8个月和12个月为时间间隔，分析该边坡软弱夹层应变增量的变化规律。

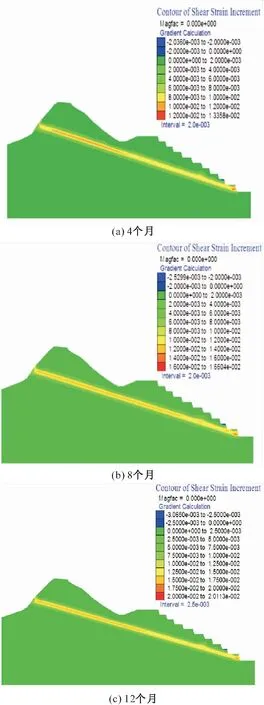
图8 某岩质边坡1-1′剖面软弱潜在滑动面剪应变增量的变化云图Fig.8 Cloud chart of shear strain increment of the 1-1 ′section as the potential sliding surface of the rock slope

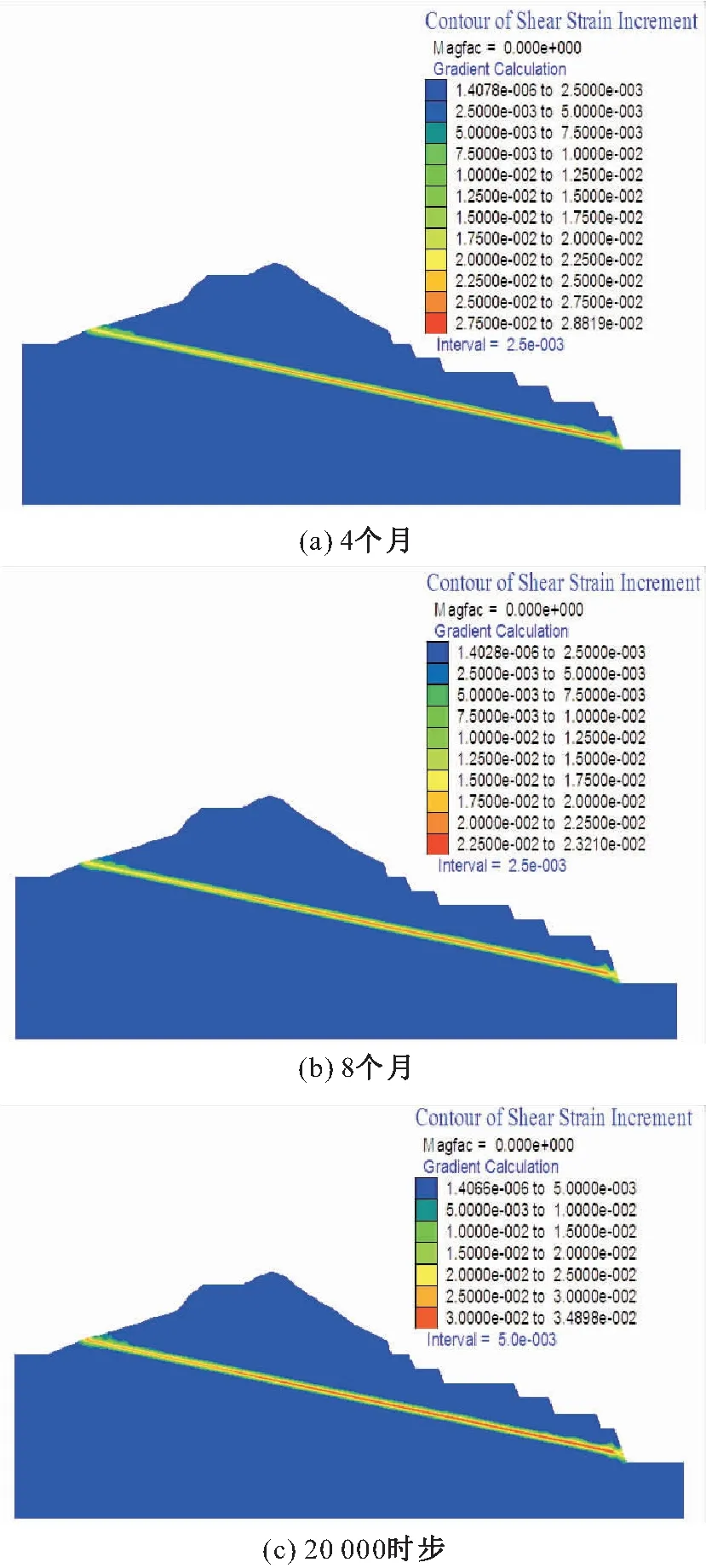
图9 某岩质边坡2-2′剖面软弱潜在滑动面的剪应变增量变化云图Fig.9 Cloud chart of shear strain increment of the 2-2′ section as the potential sliding surface of the rock slope

由图8和图9可以看出：

(1) 边坡1-1′剖面软弱潜在滑动面的剪应变增量随着预测时间的推移不断增加；4个月后，其最大剪应变增量约为1.34×10-2，分别出现在变形体滑动面的坡脚和中上部；8个月后，其最大剪应变增量继续增加，并逐步从坡顶、坡脚处向中部贯通，其剪应变增量在8个月和12个月后分别为1.66×10-2和2.01×10-2。

(2) 边坡2-2′剖面软弱潜在滑动面的剪应变增量变化与1-1′剖面类似，主要存在以下两点不同：相同时间节点下，边坡2-2′剖面软弱潜在滑动面的剪应变增量值略高于1-1′剖面，这与前述实测结果(见图6)和模型计算结果(见图7)均一致；边坡2-2′剖面软弱潜在滑动面的塑性变形区域较小，均匀分布于边坡整个潜在滑动面。由此推断，相似地质条件下，该边坡2-2′剖面位置的滑带土力学性质较差，边坡安全性较低。

综上所述，随着时间的推移，该边坡软弱夹层中的滑带土不断发生蠕变变形，这对于边坡的长期稳定性显然是不利的。根据模型计算结果可知，一年以内，该边坡潜在滑动面的剪应变增量分布尚未完全贯通，据此可以预测边坡失稳的可能性不大，但在极端自然灾害的影响下，如强降雨、地震等，边坡仍有发生滑坡的可能性。因此，建议继续加强对该边坡潜在滑动面及变形体的变形监测，并与模型预测结果进行对比，针对异常情况，及时采取有效的工程防护措施，以防止滑坡事故的发生。