基于ROC曲线与确定性系数法集成模型的三峡库区奉节县滑坡易发性评价

刘 月，王宁涛，周 超，谢家龙，李远耀

(1.中国地质大学(武汉)地质调查研究院,湖北 武汉 430074；2.中国地质调查局武汉地质调查中心(中南地质科技创新中心),湖北 武汉 430205； 3.中国地质大学(武汉)地理与信息工程学院,湖北 武汉 430074)

滑坡是我国自然灾害的主要灾种之一，对山地丘陵区的生态环境和生命财产安全构成重大威胁[1]。滑坡易发性评价是区域滑坡灾害风险评估和防控的基础，准确的滑坡易发性评价结果可为防灾减灾提供有效的技术支撑。

滑坡发育关键影响因素的选取是滑坡易发性建模的重要基础，然而至今仍未达成统一的共识，现阶段通常是在实际场地条件和资料收集的基础上，结合滑坡内部岩土体属性和外界诱发因素来选取评价指标。在滑坡易发性建模中，不同的评价指标具有不同的预测能力，即其在滑坡易发性建模中的重要性不同。不重要的评价指标会带来噪音，这些指标对滑坡易发性建模精度提升的贡献可能会弱于其噪音带来的误差，导致模型的精度降低[2]。因此，在滑坡易发性建模之前应先分析评价指标的重要性，剔除不重要的评价指标。评价指标的重要性可通过人为主观经验判断或概率统计得到，如郭子正等[3]利用逻辑回归模型公式中的回归系数对滑坡易发性各评价指标的重要程度进行了排序。受试者工作特征曲线(Receiver Operating Characteristic curve，ROC曲线)是一种有效的模型精度评价方法，可定量地分析各评价指标对滑坡易发性建模性能的影响程度。

滑坡易发性评价模型由最初的定性评价模型[4]发展到定量物理力学评价模型[5]，再到目前的概率统计模型，如信息量模型[6-9]、逻辑回归模型[10]、确定性系数模型[11]等。随着机器学习和人工智能技术的飞速发展，机器学习模型如人工神经网络模型[12-14]、支持向量机模型[12,15-17]、决策树模型[18-19]等也得到了广泛的应用。虽然机器学习模型在精度上有一定的优势，但是基于机器学习的滑坡易发性评价模型评价过程复杂，且在每次更新评价指标时都需要对整个研究区重新进行评价。而概率统计模型原理易懂、操作简单、精度较高，且在更新评价指标时只需将指标的统计系数叠加到原始评价结果中，不需再对整个研究区进行重新评价，具有较好的推广和应用价值。

本文以我国滑坡灾害高发的三峡库区奉节县为研究区，首先采用频率比方法对坡度、坡向等10个指标与滑坡发育的关系进行统计分析，通过统计结果对连续型指标进行分级并分析其对研究区滑坡发育的影响作用；然后，运用ROC曲线定量分析各评价指标对滑坡易发性建模精度的影响程度，剔除相对不重要的指标，构建对研究区滑坡易发性建模影响的关键评价指标体系；最后分别应用确定性系数法和逻辑回归模型对研究区滑坡易发性进行建模与分区。通过本研究以期结合ROC曲线法和确定性系数法的优点，构建出一套简单、准确的区域滑坡易发性评价技术方法，进一步完善滑坡灾害易发性评价理论和技术方法。

1 研究区概况

研究区奉节县隶属于重庆市，为长江三峡库区腹心之地，总面积约为4 000 km2，其地理位置见图1。县域地貌总体为东南、东北高而中部稍平缓，南北大致对称分布，以长江为对称轴，离长江越远海拔越高，零星分布少量平缓河谷平坝。该区域属中亚热带暖湿东南季风气候，在海拔600 m以下的长江河谷两岸及其阶地，气候温和，雨量充沛，日照充足，昼夜温差大。境内河流属长江水系，其中长江干流长41.5 km，另有梅溪河、大溪河、石笋河、草堂河、朱衣河等主要河流。

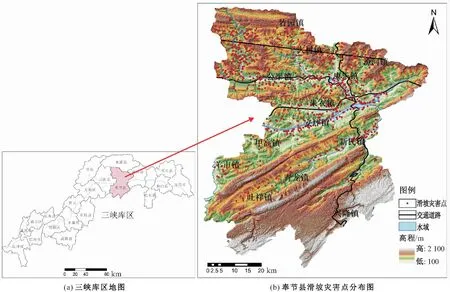
图1 研究区地理位置图Fig.1 Geographical location map of the study area

由于区域地质环境条件复杂，加上降雨充沛和受三峡库水位动态变化的影响，奉节县地质灾害频发。据三峡库区奉节县地质灾害排查资料，截止2017年奉节县共发生地质灾害1 600余处，其中滑坡1 424处，占总地质灾害的89%，已严重影响了当地经济和社会的可持续发展。本研究以奉节县为研究区，选取研究区内2006年至2017年的937处滑坡灾害点为基础数据，开展了研究区滑坡易发性评价研究。

2 研究方法

2.1 确定性系数法

确定性系数(Certainty Factor，CF)本质上是一个概率函数，主要用来计算影响地质灾害发生的各个评价因子的敏感性。该方法根据已知的地质灾害隐患点，对影响地质灾害发生的各个评价因子的不同区间进行敏感性计算，可以实现对连续型因子和离散型因子的敏感性分析。其原理公式如下：

(1)

式中：PPa为影响因子分级图层中某一特征a的条件概率，在滑坡易发性评价中表示特征a中单元存在的地质灾害隐患点的栅格数与特征a的栅格数的比值；PPs为滑坡事件在整个研究区中地质灾害发生的先验概率，可以表示为整个研究区滑坡地质灾害隐患点栅格数与研究区总栅格数的比值；CF为确定性系数，其值越大，表示滑坡灾害发生的确定性越高。

2.2 逻辑回归模型

逻辑回归(Logistic Regression，LR)模型是一种因变量满足二项分布的多元统计分析模型，通过在一个因变量和多个自变量中建立回归关系，预测某个区域某一事件发生的概率。在滑坡易发性评价中，LR模型可用于预测某一区域滑坡发生的概率。因变量即为是否发生滑坡(发生为1，未发生为0)，自变量即为参与滑坡易发性评价的各项评价指标。其原理公式如下：

Y=α0+α1X1+α2X2+…+αnXn

(2)

(3)

式中：Y为累计分布函数；α0为常数项，α1，α2，…，αn为各评价指标的逻辑回归系数；X1，X2，…，Xn为参与滑坡易发性评价的各项评价指标；P为滑坡发生的概率，其值越大，表示滑坡灾害发生的概率越高。

2.3 ROC曲线法

受试者工作特征(ROC，Receiver Operating Characteristic)曲线又称为感受性曲线，因其简单、直观的特点，可准确地反映所用分析方法特异性与敏感性的关系，具有很好的试验准确性，因而已被广泛应用于地质灾害易发性评价中[20]。在滑坡易发性评价中，1-特异度为横坐标，代表非滑坡预测为滑坡，敏感度为纵坐标，代表滑坡预测为滑坡，即可对比单个评价因子对滑坡发育的影响和重要性,也可比较不同模型下滑坡易发性评价结果的精度。ROC曲线法是通过ROC曲线下面积(Area Under Curve，AUC)来反映和比较模型的评价预测精度，当AUC值小于0.7表示模型的评价精度较差，当AUC值为0.7～0.8表示模型的评价精度中等，当AUC值为0.8～0.9表示模型的评价精度较好，当AUC值在0.9以上表示模型的评价精度非常好[21]。

3 研究区滑坡易发性评价

3.1 滑坡易发性评价的流程

本文以滑坡灾害高易发区三峡库区奉节县为研究区，首先在实际场地条件和资料收集的基础上，初步选取坡度、坡向、高程、剖面曲率、断裂带距离、岩土体类型、水系距离、降雨量、道路距离和植被覆盖度10项基本指标，建立滑坡易发性初始评价指标体系，并采用频率比法对连续型指标进行科学分级；然后，运用ROC曲线法剔除不重要的评价指标，建立研究区滑坡易发性评价的关键评价指标体系；最后，分别运用确定性系数法和逻辑回归模型对研究区滑坡易发性进行评价与分区，并对比分析两种模型的滑坡易发性评价结果的精度。具体评价流程见图2。

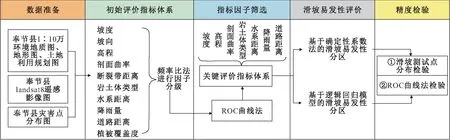
图2 滑坡易发性评价流程图Fig.2 Flow chart of evaluation of landslide susceptibility

3.2 评价单元的划分

评价基础单元的合理划分对滑坡易发性评价结果有着直接的影响。目前，常用的评价单元有栅格单元、地域单元、均一条件单元、斜坡单元和地形单元等。其中，地域单元、均一条件单元、斜坡单元和地形单元均较适合小范围大比例尺的区域，而研究区面积达到4 000 km2，选用大小相同的栅格单元更适合，既能提高评价效率也能满足评价精度的要求。确定栅格单元大小的计算公式如下[22]：

Gs=7.49+0.000 6S-2.0×10-9S2+2.9×10-15S3

(4)

式中:Gs为适宜的网格大小(m);S为比例尺分母。

根据计算结果可知,研究区最佳栅格单元大小为50.4 m，本文最终选取50 m×50 m栅格作为基础评价单元。研究区域共划分为1 626 035个栅格，滑坡所占栅格数为28 890个。

3.3 初始评价指标体系的构建

首先，结合研究区野外调查和以往的研究成果[2]，初步选取坡度、坡向、高程、剖面曲率、断裂带距离、岩土体类型、水系距离、降雨量、道路距离和植被覆盖度10项指标;然后，采用滑坡相对频率比法对各评价指标进行等级划分，提高评价指标分级准确性[10]。滑坡相对频率比(FR)表示评价指标各区间对滑坡易发性影响的重要程度，定义如下：

(5)

FR>0表示该分类区间利于滑坡发生；FR<0表示该分类区间不利于滑坡的发生。对FR值相近的区间进行合并，将各评价指标进行等级划分，见图3。

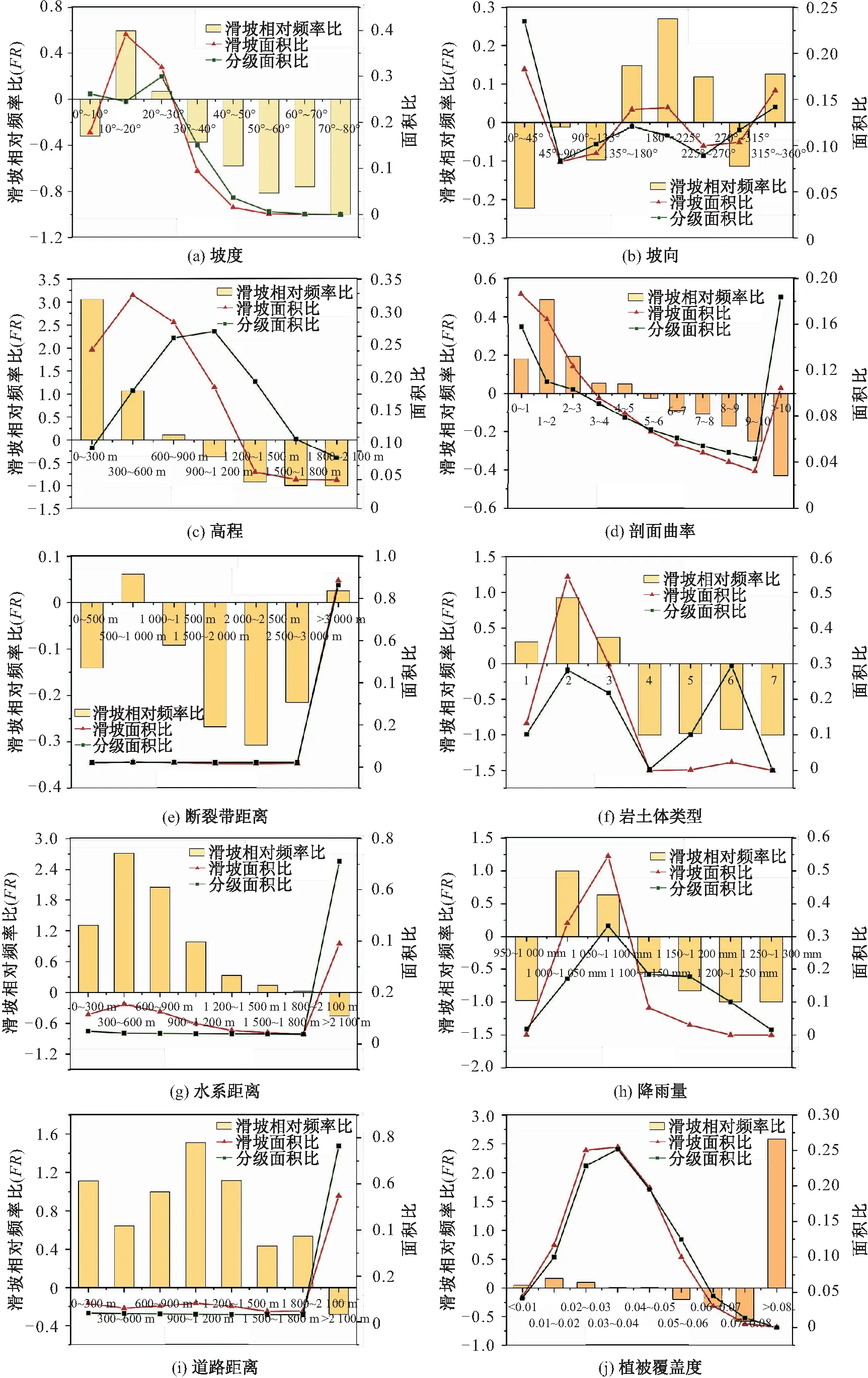
图3 滑坡易发性各评价指标的滑坡相对频率比图Fig.3 Relative frequency ratio chart of each factor for landslide susceptibility evaluation

坡度、坡向、高程和剖面曲率均从DEM中直接提取，为连续型评价指标，对各评价指标进行等步长离散化。各评价指标的具体分级如下：

(1) 坡度：不同坡度，斜坡的应力分布、水文条件、人类工程活动等存在差异，从而影响滑坡的发育[23]。研究区内坡度以中缓坡为主，主要分布在0°～30°。

采用频率比法对研究区坡度进行分级，先以10°为间隔，划分为8个等级，由图3(a)可见,在坡度为10°～20°时，滑坡FR值最大，利于滑坡的发生。因此，最终将研究区坡度分为4级：0°～10°、10°～20°、20°～30°、>30°。

(2) 坡向：不同坡向，光照条件不同，导致植被覆盖度和地表径流等存在差异，从而影响斜坡的稳定性。研究区内坡向主要集中在0°～45°。采用频率比法对研究区坡向进行分级，先以45°为间隔，划分为8个等级，由图3(b)可见，在坡向为135°～270°时，滑坡FR值较大，利于滑坡的发生。因此，最终将研究区坡向分为5级：0°～45°、45°～135°、135°～270°、270°～315°、315°～360°。

(3) 高程：不同高程，植被类型、土壤类型、地表集水能力和人类工程活动等存在差异，从而间接影响滑坡的发育。研究区内高程主要集中在300～1 500 m。采用频率比法对研究区高程进行分级，先以300 m为间隔，划分为7个等级，由图3(c)可见，在高程为0～900 m时，滑坡FR值大于0，利于滑坡的发生。因此，最终将研究区高程分4级：0～300 m、300～900 m、900～1 200 m、1 200～2 100 m。

(4) 剖面曲率：剖面曲率反映了坡面形态，不同的坡面形态坡体物质的搬运沉积情况不同，从而影响滑坡的发育。采用频率比法对研究区剖面曲率进行分级，先以1为间隔，划分为11个等级，由图3(d)可见，在剖面曲率为0～5时，滑坡FR值大于0，利于滑坡的发生。因此，最终将研究区剖面曲率分为5级：0～1、1～2、2～5、5～10、>10。

(5) 断裂带距离：研究区断裂带及其周边一定范围内的岩土体遭受破坏，坡体的完整性降低，从而影响坡体的稳定性。采用频率比法对研究区断裂带距离进行分级，先以500 m为间隔分为7级，由图3(e)可见，在距断裂带500～1 000 m的区域，滑坡FR值较大，利于滑坡的发生。因此，最终将研究区断裂带距离分为5级：0～500 m、500～1 000 m、1 000～1 500 m、1 500～3 000m、>3 000 m。

(6) 岩土体类型：岩土体类型是孕育滑坡发生的重要内在因素。采用频率比法对研究区岩土体类型进行分级，分为7级。岩土体类型中，1表示以坚硬厚层砂岩为主的岩组；2表示软硬相间层状砂岩、黏土岩互层岩组；3表示弱岩溶化软硬相间层状碎屑岩夹碳酸盐岩岩组；4表示中等岩溶化软硬相间层状碳酸盐岩碎屑岩互层岩组；5表示中强岩溶化软硬相间层状碳酸盐岩夹碎屑岩岩组；6表示强岩溶化坚硬层状碳酸盐岩岩组；7表示以软弱层状黏土岩为主的岩组。由图3(f)可见，研究区滑坡主要发育在软硬相间层状砂岩、黏土岩互层岩组之上。

(7) 水系距离：研究区库水位的动态变化以及水流对坡脚的冲刷、侵蚀作用破坏了斜坡的稳定性，造成滑坡多沿水系分布。采用频率比法对研究区水系距离进行分级，先以300 m为间隔，划分为8级，由图3(g)可见，在距水系距离为0～2 100 m时，滑坡FR值较大，利于滑坡的发生。因此，最终将研究区水系距离分为4级：0～300 m、300～900 m、900～2 100 m、>2 100 m。

(8) 降雨量：降雨是滑坡发生的重要诱发因素之一。通过全区的降雨量等值线，采用频率比法对研究区降雨量进行分级，由图3(h)可见，在降雨量为1 000～1 100 mm时，滑坡FR值大于0，利于滑坡的发生。因此，最终将降雨量划分为4级：950～1 000 mm、1 000～1 100 mm、1 100～1 200 mm、1 200～1 300 mm。

(9) 道路距离：在道路建设过程中不合理地开挖坡脚等常会引起边坡失稳，促进滑坡的发育。采用频率比法对研究区道路距离进行分级，先以300 m为间隔，划分为8级，由图3(i)可见，在距道路距离为0～2 100 m时,滑坡FR值较大，利于滑坡的发生。因此，最终将研究区道路距离分为5级：0～300 m、300～600 m、600～1 500 m、1 500～2 100 m、>2 100 m。

(10) 植被覆盖度：由于植被根茎的固土作用，植被覆盖度不同，斜坡的稳定性存在差异。在ENVI中对下载的Landsat 8遥感影像数据进行处理得到植被覆盖度指数，并在ArcGIS中进行重分类，以0.01为间隔，划分为9类，由图3(j)可见，在植被覆盖度>0.08时，滑坡FR值较大，利于滑坡发生。因此，最终将研究区植被覆盖度分为3级：<0.05、0.05～0.08、>0.08。

3.4 基于ROC曲线法与确定性系数法集成模型的滑坡易发性评价

将ROC曲线法与确定性系数法相结合，在滑坡易发性评价过程中，先选取确定性系数法计算出不同评价指标各分级状态下的确定性系数(CF)值，并利用ROC曲线法定量确定各评价指标的重要程度排序；然后在此基础上按重要程度由小到大逐步剔除不重要的评价指标，并将剩余评价指标按CF值叠加计算出一次滑坡易发性评价结果；最后利用ROC曲线法比较滑坡各易发性评价结果的精度。在滑坡易发性评价结果的精度达到峰值时的评价指标体系即为关键评价指标体系，关键评价指标体系下的滑坡易发性评价结果为研究区最终的滑坡易发性分区。

ROC曲线法确定关键评价指标体系的首要任务是确定所有评价指标的重要程度排序。利用ROC曲线法对评价指标进行重要程度排序，首先是要计算各评价指标不同分级状态下的CF值，其计算结果见表1。

表1 滑坡易发性各评价指标的确定性系数(CF)Table 1 Certainty Factor(CF) of each factor for landslide susceptibility evaluation

由表1可知，研究区滑坡主要发育在海拔低于300 m、植被覆盖度较高以及距水系距离在300～900 m的区域，与历史滑坡灾害点分布情况相符。

以全区所有滑坡点和等量非滑坡点(发生滑坡为1；未发生滑坡为0)作为状态变量，对应的各评价指标不同分级状态下的CF值作为检验变量，利用ROC曲线法进行分析，并根据AUC值的大小对各评价指标重要程度进行排序，见图4。

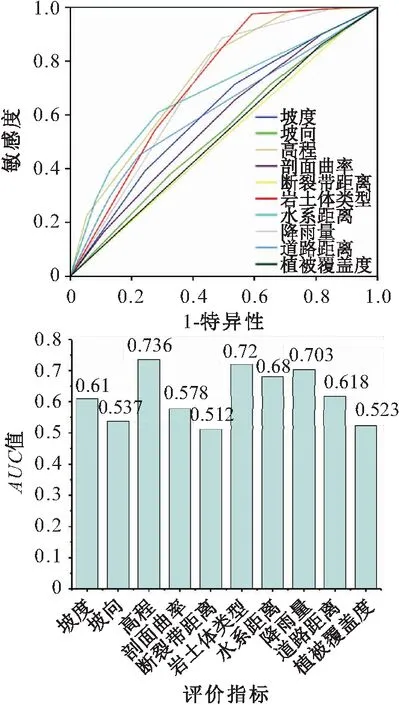
图4 研究区滑坡易发性各评价指标ROC曲线分析图Fig.4 Diagram of ROC curve analysis of each factor for landslide succeptibility evaluation of the study area

由图4可见，对研究区滑坡发育影响最大的评价指标是高程，对研究区滑坡发育影响最小的评价指标是断裂带距离。研究区滑坡易发性各评价指标重要程度的排序为高程>岩土体类型>降雨量>水系距离>道路距离>坡度>剖面曲率>坡向>植被覆盖度>断裂带距离。

首先对研究区滑坡易发性初始评价指标体系中评价评价指标按重要程度由小到大逐步剔除不重要的评价指标，并将剩余评价指标按CF值叠加计算出一次滑坡易发性评价结果；然后选取70%的滑坡作为训练样本，剩余的30%作为测试样本，并在非滑坡面上随机生成等量的非滑坡训练样本和测试样本；最后利用ROC曲线法分析各次滑坡易发性评价结果的成功率和预测率，见图5。

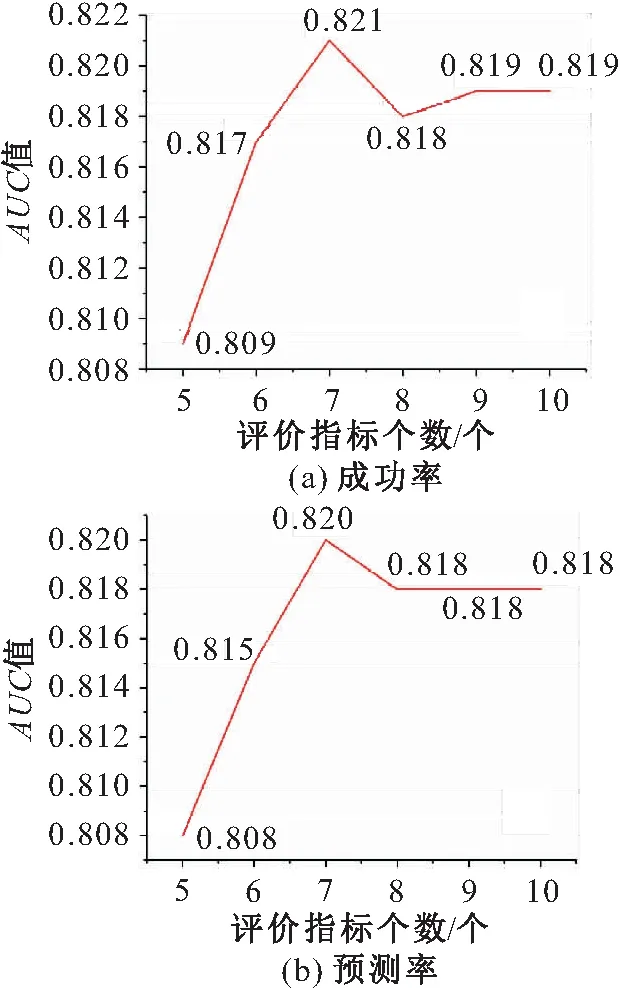
图5 研究区滑坡易发性不同评价指标体系评价 结果的精度对比图Fig.5 Comparison of accuracy of different index systems for landslide succeptibility evaluation of the study area

由图5可见，当评价指标个数为7个时，研究区滑坡易发性评价结果的成功率和预测率分别为0.821和0.820，均达到最高。因此，研究区滑坡易发性的关键评价指标体系由坡度、高程、剖面曲率、岩土体类型、水系距离、降雨量和道路距离7个评价指标构成。

3.5 基于逻辑回归模型的滑坡易发性评价

本文利用确定的滑坡易发性关键评价指标体系并基于逻辑回归模型对研究区滑坡易发性进行了评价。以70%的滑坡及等量的非滑坡作为训练样本，是否发生滑坡(发生为1，未发生为0)作为因变量，各评价指标不同状态下的归一化值作为自变量，在SPSS软件中进行二元逻辑回归分析。本文使用滑坡发生率对各评价指标进行归一化处理，其归一化处理公式如下[24]：

(6)

(7)

式中：ALij为第i个一级评价指标中第j个二级评价指标内的滑坡面积(m2)；ATij为第i个一级评价指标中第j个二级评价指标的区域总面积(m2)；dij为第i个一级评价指标中第j个二级评价指标的滑坡发生概率；n为一级评价指标总数(个)；m为二级评价指标总数(个)；Iij为第i个一级评价指标中第j个二级评价指标的滑坡发生概率的归一化值。

拟合得到的逻辑回归方程如下：

Y=-5.202+2.721X1+1.761X2+4.656X3+5.288X4+2.295X5+1.348X6+2.170X7

(8)

式中:X1～X7依次为坡度、高程、剖面曲率、岩土体类型、水系距离、降雨量和道路距离。

基于公式(2)和(3)在Arcgis中利用栅格计算器计算研究区所有栅格的滑坡发生概率，从而得到了全区滑坡易发性分区。

3.6 模型精度的对比分析

本文将利用确定性系数法和逻辑回归模型所得到的研究区滑坡易发性评价结果，采用自然断点法将其分为高易发区、较高易发区、较低易发区和低易发区4级，从而得到三峡库区奉节县滑坡易发性分区图，见图6。

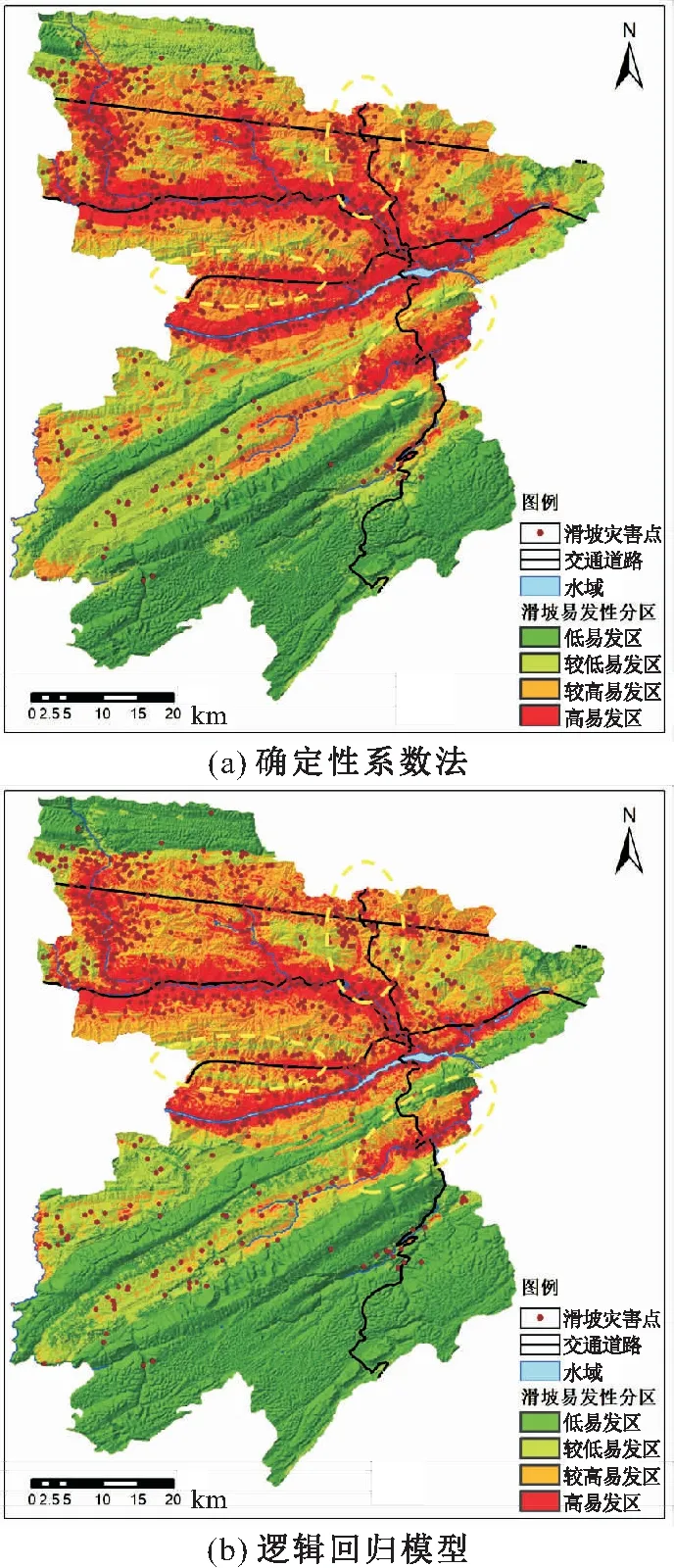
图6 三峡库区奉节县滑坡易发性分区图Fig.6 Landslide susceptibility zoning map of Fengjie County in Three Gorges Reservoir

由图6可见，研究区滑坡高易发区主要是沿水系、道路分布，与历史滑坡灾害点的分布情况一致；确定性系数法下的研究区滑坡高易发区沿道路分布的特征较逻辑回归模型更为明显(见图中标注处)。

3.6.1 模型合理性检验

本文通过统计测试样本在研究区滑坡各易发性分区中的分布，来检验模型的有效性和科学性，其统计结果见表2和图7。其中，滑坡比率Ri[25]为某滑坡易发性分区内滑坡栅格数占总滑坡栅格数的比例与该分区总栅格数占总研究区栅格数比例的比值，反映了滑坡在各个易发性分区中的强度。当Ri满足下式时，表明滑坡易发性分区图有效，且R1值越小、Rn值越大，说明滑坡易发性评价结果越理想。

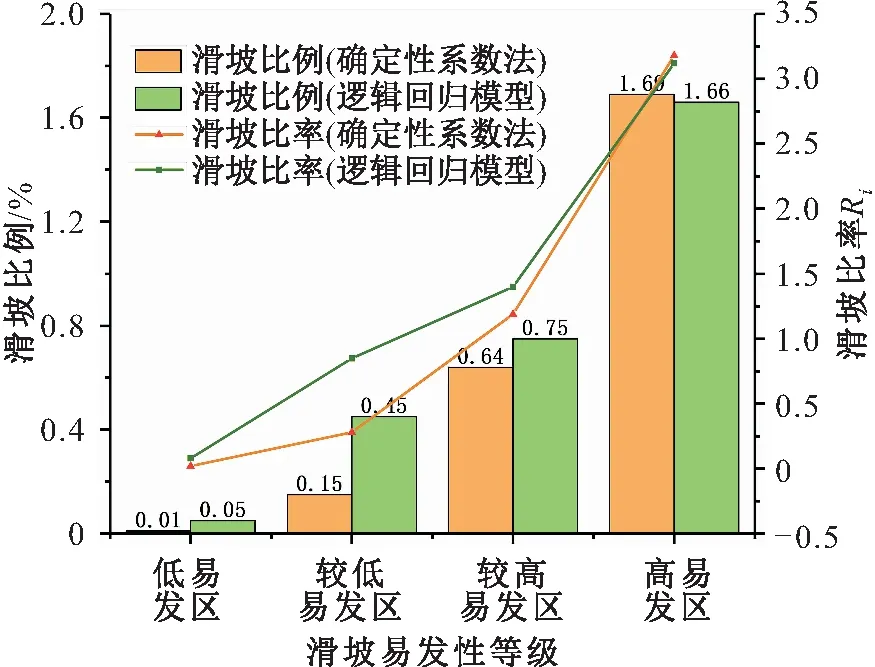
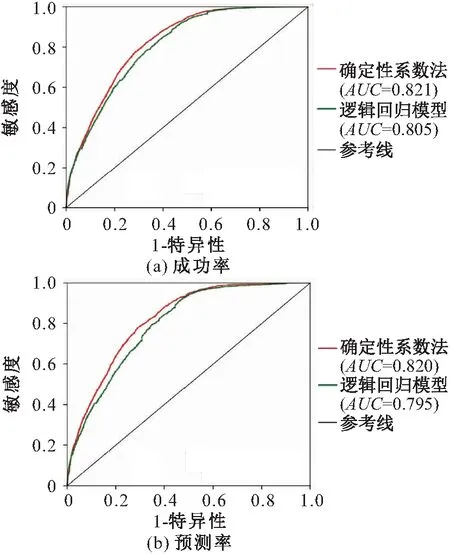
R1

(9)

其中，下标1～n表示滑坡易发性等级由低到高。

由表2和图7可知，利用确定性系数法和逻辑回归模型确定的研究区滑坡易发性分区图中滑坡比例依次增大，说明两种模型的分区均合理；确定性系数法确定的研究区滑坡低易发区的Ri值为0.02，其值小于逻辑回归模型的0.08，确定性系数法确定的研究区滑坡高易发区的Ri值为3.18，其值大于逻辑回归模型的3.12；确定性系数法中有92.24%的滑坡分布在高易发区和较高易发区，其值高于逻辑回归模型的80.65%，表明确定性系数法确定的研究区滑坡易发性分区结果更为理想。

表2 研究区滑坡栅格统计结果表Table 2 Statistical results of landslide grids of the study area

图7 两种模型的滑坡易发性等级对比Fig.7 Comparison of different levels of landslide susceptibility between two models

3.6.2 基于ROC曲线法的模型精度分析

本文在SPSS软件中对两种模型获得的滑坡易发性评价结果进行ROC曲线分析，两种模型的精度对比结果见图8。

图8 两种模型的成功率及预测率曲线对比Fig.8 Comparison of success rate curves and prediction rate curves between two models

由图8可见，确定性系数法的成功率和预测率为82.1%和82.0%，其值优于逻辑回归模型的80.5%和79.5%。

4 结 论

(1) 本文以三峡库区奉节县为研究区，结合实际场地条件和资料收集情况，选取了坡度、坡向、高程、剖面曲率、断裂带距离、岩土体类型、水系距离、降雨量、道路距离和植被覆盖度10项基本指标，建立了研究区滑坡易发性初始评价指标体系，并利用频率比法对各评价指标进行分级，计算各评价指标不同分级状态下的频率比值，在坡度为10°～20°、高程低于300 m、岩土体类型为软硬相间层状砂岩、黏土岩互层岩组时，滑坡频率比值较高，易于滑坡发育。

(2) 采用ROC曲线法剔除了断裂带距离、植被覆盖度和坡向3个评价指标，从而构建了对研究区滑坡发育影响的关键评价指标体系，按评价指标的重要程度排序为：高程>岩土体类型>降雨量>水系距离>道路距离>坡度>剖面曲率，与三峡库区滑坡多为降雨性滑坡且由于库水位动态变化、长江两岸滑坡较为发育这一实际情况相符。当剔除坡向、植被覆盖度和断裂带距离3个评价指标时，模型的预测精度最高，为0.82。

(3) 对确定的研究区滑坡易发性关键评价指标体系，分别运用确定性系数法和逻辑回归模型对研究区滑坡易发性进行评价，结果表明：确定性系数法确定的研究区滑坡低易发区的滑坡比率较逻辑回归模型更小，确定的研究区滑坡高易发区的滑坡比率较逻辑回归更大；确定性系数法中有92.24%的滑坡分布在高易发区和较高易发区，其值高于逻辑回归模型的80.65%；确定性系数法的成功率和预测率为82.1%和82.0%，其值高于逻辑回归模型的80.5%和79.5%。上述结果表明通过集合ROC曲线法和确定性系数法的优点构建的这一套简单、准确的区域滑坡易发性评价技术方法，具有可靠性和精确性，可为进一步完善滑坡灾害易发性评价理论和技术方法提供依据。