挡风墙对近地面光伏板风压的影响研究
2020-08-14张大千吴康宁
张大千,吴康宁
(沈阳航空航天大学 航空宇航学院,沈阳 110136)
我国的《建筑结构荷载规范》和美国的ASCE/SEI 7-10(American Society of Civil Engineers)针对光伏发电系统的设计只给出了极限状态下光伏板面上的体型系数,并没有详细研究不同环境和复杂风场对光伏板面风压的影响。因此,国内外不少学者采用风洞实验和计算机模拟的方法,对复杂环境下光伏板面的风压分布情况进行了研究。
文献[1]~[9]运用风洞实验技术,探究了风向角、光伏板面安装倾角、光伏阵列间距以及光伏系统上的电池组块缝隙对近地面安装的光伏系统的光伏板面的平均风压和极值风压的影响。
随着计算机运算能力的提高和CFD技术的成熟,CFD数值模拟的结果越来越准确,因此不少学者运用CFD技术对太阳能电池板面的风压进行了数值模拟。文献[10]~[15]采用k-ωSST和RANS模型,对光伏系统电池板面的风压分布情况进行了数值模拟,所得的计算结果与相应的风洞实验结果具有较好的一致性。
目前,光伏发电站中常出现光伏支架因强风损坏的情况,此时若重新设计支架系统成本很高,为此,常设置挡风墙来阻挡来流大气,以减缓作用在光伏板面上的风压。但目前针对挡风墙对近地面光伏板面风压影响的研究并不多见,为此,本文探究了不同位置和不同组合下的挡风墙,对来流大气的阻挡作用,为光伏结构抗风设计提供参考。
1 几何参数
图1为计算模型示意图,其中图1a为光伏板,图1b为光伏阵列与挡风墙,图中各符号具体解释见表1。其中模型一与文献[1]中光伏板实际尺寸相同,模型二的几何尺寸来自于某厂商提供的光伏系统。借鉴文献[14]~[15],在建模过程中忽略光伏支架,仅对太阳能电池板进行建模。结合文献[16]电池板间隙对板面风压影响的研究,忽略了模型一和模型二光伏系统的电池板间间隙,将多个单块太阳能电池板组合成的电池板面设计成一个矩形平板。光伏阵列的纵向与横向间距均按照实际情况设计,分别为3 m、1 m。
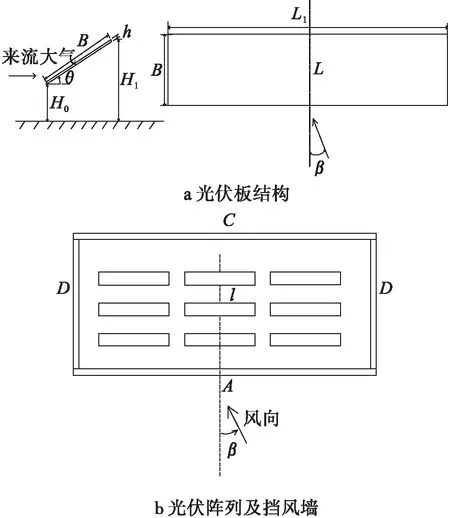
图1 计算模型

表1 计算模型符号表
图2为流场域侧视图,本文采用长方体流场域,根据文献[17]对大气边界层流场域的规定,挡风墙与光伏系统组成的几何模型距离入口24 m,距离出口72 m,距离流场域两侧边界均为45 m。几何模型在流场域横截面上的最大面积,估算为正面挡风墙,墙体长度38.9 m和高度2.4 m下的阻塞面积,约为93.36 m2,此种情况下所对应的流场域最大阻塞率为2.07%,小于文献[17]中规定的阻塞率不可大于3%的要求。
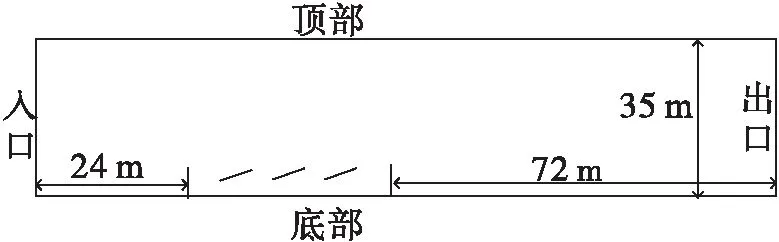
图2 计算流场域
以下工况从不同的角度探究挡风墙对光伏板面风压的减缓作用。工况1探究正面的挡风墙,工况2探究正面挡风墙与侧面挡风墙混合作用,工况3探究正面挡风墙与背面挡风墙混合作用,工况4探究四面墙体包围下的光伏板面风压分布情况。

表2 计算工况
2 边界条件与求解器设置
为更好模拟太阳能电池板面的风压变化情况,首先需要对光伏系统身处的大气边界层环境进行建模,为此需要对流场域的边界条件进行特殊的设置。具体设置情况如下:
入口边界条件:参考文献[10]~[13],要求模拟大气边界层时,在来流入口处,沿垂直于流场底面方向,平均风速要以一定的梯度变化。现国内外规范中规定的平均风速曲线有对数数律曲线和指数数律曲线两种,根据文献[18]本文选用对数数律曲线,曲线具体方程如下
(1)
y为距离流场域底部垂直高度;
U(y)为与流场域底部垂直高度为y米处的平均风速;
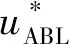
κ为卡门常数,本文取0.41;
y0为粗糙度长度,根据文献[19],B类风场取0.03 m。
因本文选用的数值模型为k-ωSST模型,为闭合方程组,还需要在入口处设置湍流强度k和比耗散率ω,根据文献[18]、[20]湍流动能k和比耗散率ω设置如下
(2)
k(y)为与流场域底部垂直高度为y米处的湍流强度;
Cμ为k-ε模型常数,本文取0.09。
(3)
ε(y)为与流场域底部垂直高度为y米处湍流耗散率。
ω=ε(y)/Cμk(y)
(4)
ω为湍流比耗散率。
出口边界条件:根据文献[10]、[11]、[18],在模拟近地面安装的光伏系统时采用的出口边界条件,本文将出口边界条件设置为OUTFLOW。出口与入口均设置一个大气压作为参考压。
流场域边界条件设置:根据文献[18],在模拟大气边界层时,需保证入口处和模型处流场域的湍流特性基本相同,为此需在FLUENT中做如下的边界条件处理。
在流场域的底部无滑移边界条件的基础上,设置如下参数:
底部粗糙度高度
(5)
Cs为粗糙度系数,根据文献[18]的建议,本文取0.7。
沿流向的剪切应力
(6)
ρ为空气密度,本文取1.293 kg/m3。
为了避免流场域顶部对各参数曲线的影响,结合文献[10]、[11]、[13]、[18],本文将流场域顶部设置为滑移壁面,速度方向与入口处速度方向相同,速度大小为24.3 m/s。
墙体和光伏板表面边界条件:结合文献[10]~[13]、[21]、[22],在模拟顿体绕流时设置的边界条件,本文在两侧流场域壁面,挡风墙和光伏系统表面采用无滑移边界条件。上述边界条件中采用的壁面函数均为标准壁面函数。
本文选用压力基隐式求解器,采用压力速度耦合SIMPLE算法,考虑到本文采用的是四面体与六面体混合网格,在光伏系统表面采用的是棱柱边界层,变量梯度采用Green-Guass Node-Based,压力采用二阶格式,动量项、湍流动能和湍流耗散率均采用二阶迎风格式。各变量的收敛级数均设置为10-6,多次迭代直至结果收敛。
图3给出了流场域中入口处于墙体处的湍流参数曲线对比图。从图3中可以看出,在流场域中平均风速具有良好的稳定性,湍流强度除流场域顶部处受壁面扰动稳定性差外,远离顶部流场域处的湍流强度也具有良好的稳定性,基本满足文献[18]提出的大气边界层模拟要求。
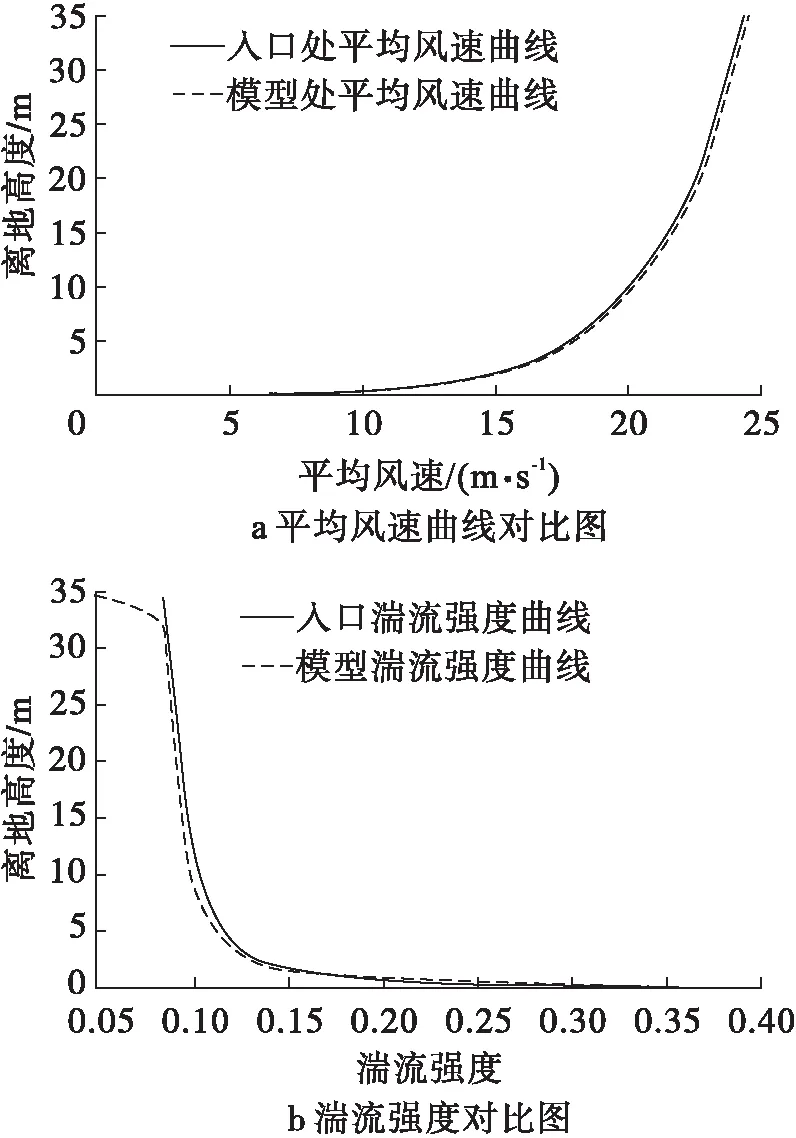
图3 入口处与模型处湍流特性对比图
3 网格划分与数据处理
本文采用混合网格进行划分,在远离模型处采用六面体网格,在模型周围采用四面体网格,并在光伏板面附近设置边界层网格。本文对光伏板面和墙体附件的网格进行了多次加密,以工况1进行网格自适应检验,第一种网格划分情况如下:挡风墙附近采用六面体网格,沿挡风墙长度方向生成60个节点,宽度方向生成3个节点,沿高度方向生成12个节点,并在挡风墙表面设置第一层高度为6 mm、增长率为1.2的10层边界层网格。在光伏板附近采用三棱柱网格,光伏板上下版面最大尺寸为0.3 m,框体表面最大网格为0.08 m,并设置第一层高度为4 mm、增长率为1.2的10层边界层网格。第二种与第三种网格划分:对上述设置参数(除边界层设置外)进行加倍处理,并以上下光伏板面风压系数为验算参考依据。通过对比发现,第一次与第二次的风压系数最大误差达到5.2%,第二次与第三次的风压系数最大误差达到1.3%。参考文献[10]~[15]的经验,选取第二种网格划分方式对后续工况进行网格划分。
数值模拟准确性验证中采用无量纲对比形式,数据具体处理情况如下
(7)
式(7)中,Cp为板面风压系数;ppi为板面网格单元i中心处的风压,风压均沿板面法向指向板面为正,背离板面为负;p0为入口处设置的参考压,U为模型离地最低高度处水平风速。
4 结果分析
4.1 数值模拟方法验证
取模型一上下板面中心线L处数值模拟结果与文献[1]相应处风洞实验结果进行对比,以验证数值模拟的准确性,对比结果如图4所示。从图4中可以看出0°风向下光伏板上板面的数值模拟结果与风洞试验的结果基本一致,而0°风向角光伏板的下表面,数值模拟与风洞试验的结果略有误差,结合风洞实验经验,推测可能是由于风洞实验中模型下表面的风压测压管扰动导致。但变化趋势相同。由此可知,采用CFD数值模拟方法,计算近地面安装的光伏板风荷载是可行的。

注:b为上板面流体网格单元中心到上板面底部边界的距离
4.2 无挡风墙下的光伏阵列
图5a、图5b为无挡风墙下的光伏阵列上板面和下板面的风压分布云图,图5c为沿中轴线截取的光伏板周围的流线图。从图5中我们可以看出,在0°风向角下,光伏阵列板面风压分布沿中轴线呈现出对称分布,这与文献[1]~[3]的风洞实验结果相一致。从图5a、图5b中可以看出,板面最大正压和最大负压均出现在第一排光伏板的底部附近,从图5c可以看出,这是由于第一排阵列与第二排阵列之间形成了一个较大的漩涡,且气流漩涡中心相对于第一阵列下板面的底部较近的缘故。而第二排与第三排阵列之间无漩涡出现,但受到第二排对来流大气的阻挡,部分近地面的气流从新回流到第三排阵列的底部附近,使得第三排阵列上板面底部附近从新出现正压 ,而后来流大气绕过第三排阵列,在其后又出现一个新的漩涡,此漩涡随着来流大气发散较快,因此第三排光伏板下板面产生的负压值相对于第一排明显较小。因此,在设置挡风墙时,应当首先考虑减缓大气来流方向对第一排光伏阵列的作用。
4.3 挡风墙A下的光伏阵列
图6a、图6b分别为上下板面风压分布云图,从图6a、图6b中可以看出,与无挡风墙相比,正面挡风墙A明显改善了整个光伏阵列风压分布的格局,其中第一排光伏阵列上板面的底部区域风压由正压变为了负压,且压强的最大值从60 Pa减小为50 Pa,而背面风压变为了正压。同时上下板面风压分布均匀,这使得作用在支架结构上的扭矩大大减小。第二排与第三排光伏阵列上下板面均呈现出正压分布,且分布比较均匀,这使得上下板面风压差形成的板面压力和支架结构上的扭矩更小,与无挡风墙相比,挡风墙的出现大大减少了来流大气作用在光伏阵列上的压力。图6c给出了沿中轴线截取的光伏板周围的流线图,与图5c相比,正面挡风墙的出现使得大量的气流绕光伏板顶部流过,再从光伏板的底部附近绕流回到墙体背面,在墙体的背面形成较大的空气漩涡,这使得气流不再直接作用在光伏板上,从而大大减缓了光伏板面上的压力。

图5 无挡风墙光伏阵列板面风压分布云图与阵列截面流线图
4.4 挡风墙AC组合
图7a、图7b分别为上下板面风压分布云图,从图7a、图7b中可以看出,与单独正挡风墙A相比,当风墙AC组合,使得第三排光伏阵列上板面的正风压向板两侧压缩,正压明显减小,且光伏阵列上板面的压强大小明显减弱。但第三排光伏阵列中,8号光伏板的下板面沿中轴线附近出现较大的正压,通过图7c我们发现,这是由于挡风墙C后出现一个较大的漩涡,使得大量的气流回流到挡风墙C的上方,同时又与来流的大气相互作用,使得大量的气流流向了8号板的下板面,因此在此处形成了较大的下板面正压分布。与此同时,通过对比图7a、图3b和图6a、图6b,我们可以发现,挡风墙C的出现,有效减小了光伏阵列板面压强的最大值,使得上下板面压强差形成的板面整体压力进一步减小,因此可以看出,单独设置一个挡风墙A是远远不够的。
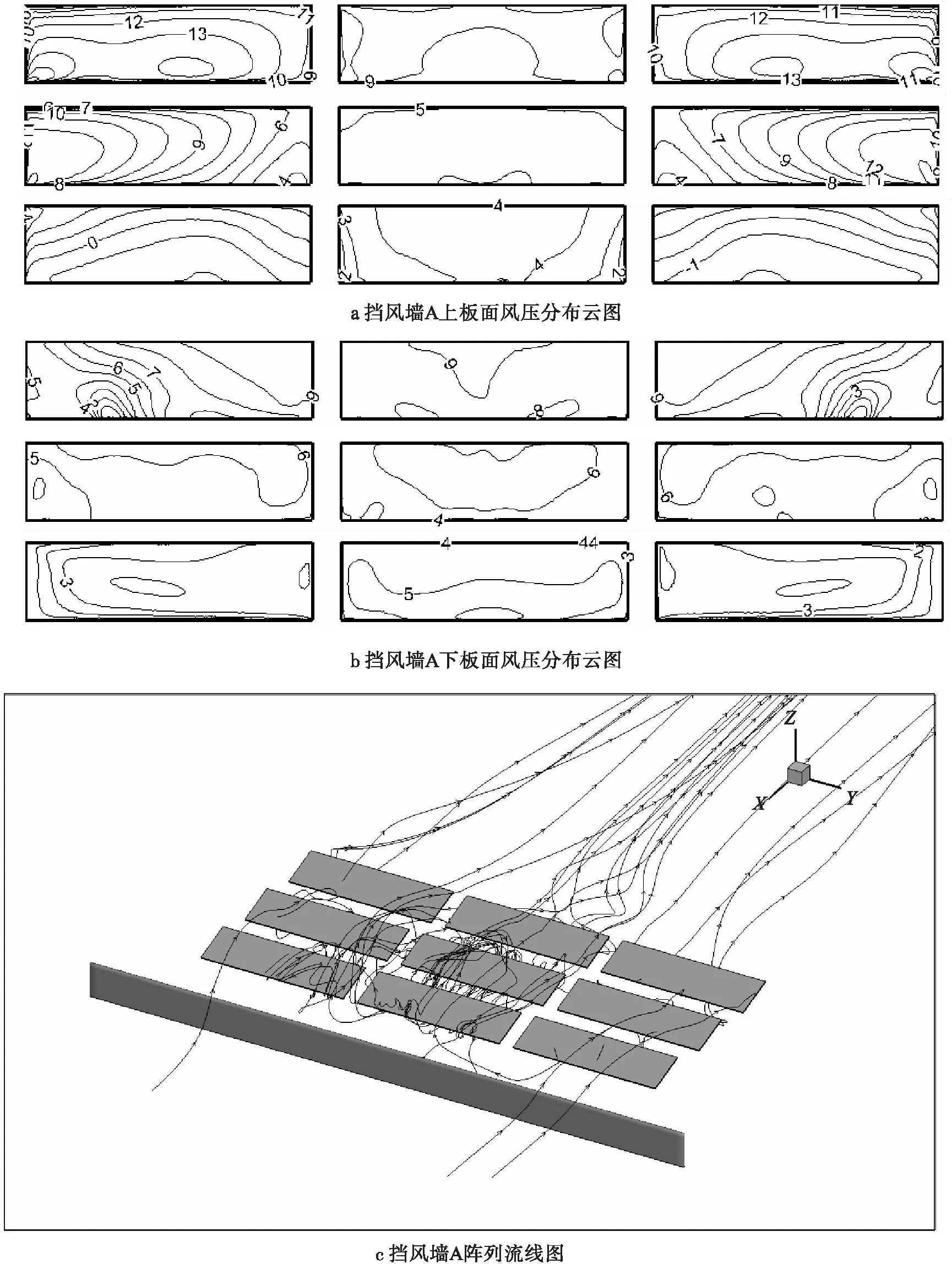
图6 挡风墙A光伏阵列板面风压分布云图与阵列截面流线图

图7 挡风墙AC光伏阵列板面风压分布云图与阵列截面流线图
4.5 挡风墙AD组合
图8a、图8b分别为上下板面风压分布云图,从图8a、图8b中可以看出,与挡风墙AC组合相比,挡风墙AD组合上下板面风压分布呈现出沿中轴线向两侧降低的趋势。与此同时,挡风墙AD组合明显降低了光伏板上下板面的压强差,这使得光伏板面作用的压力值明显降低。从图9c可以看出,由于挡风墙D的出现,使得第三排光伏阵列的上下板面附近均出现大气漩涡,而且第一排与第二排光伏阵列之间的大气漩涡明显上移,远离了光伏阵列。为此,在某些光伏发电站处于风向常年较固定的地区中,采用挡风墙AD组合进行挡风墙设置不失为一种较好的选择。但光伏阵列板面的压强最大值改善并不明显,尤其在第三排光伏阵列的两侧底部边缘附近出现了局部较大的上下板面压强差,这使得第三排光伏板阵列两侧光伏板的局部边缘处压力较大,容易造成破坏。
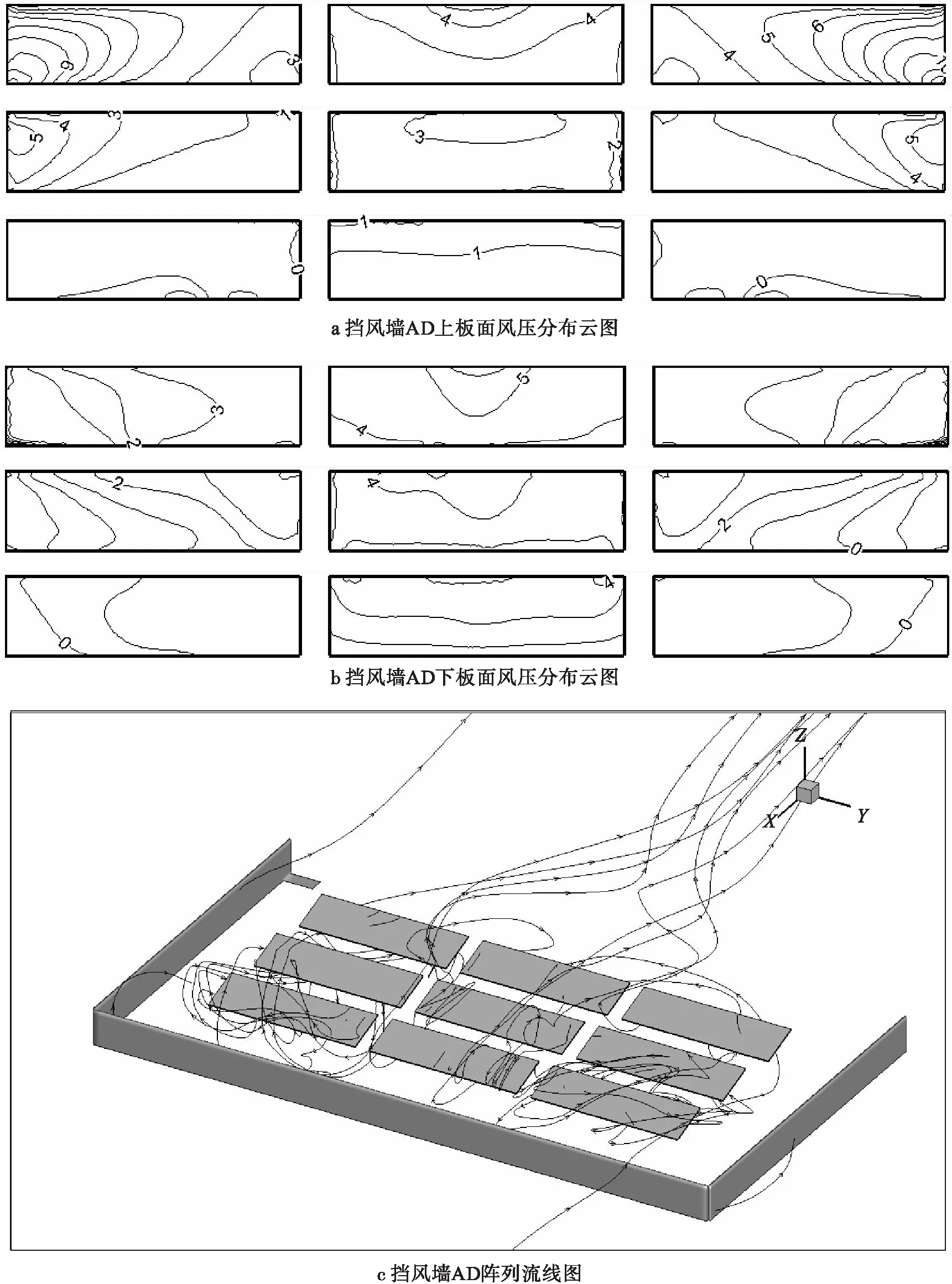
图8 挡风墙AD光伏阵列板面风压分布云图与阵列截面流线图
4.6 挡风墙ADC组合
图9a、图9b分别为上下板面的风压分布云图,从图9a、图9b中可以看出,挡风墙ABC组合明显拥有上述所有组合的特点。与此同时从图9c可以看出,挡风墙D的出现使挡风墙AC组合中出现第三排光伏板后的大气漩涡明显后移,这使得回流到第三排光伏阵列下板面的气流明显减少,与此同时,由于挡风墙C的出现,挡风墙AD组合中出现在光伏阵列顶部附近的大气漩涡明显减小,且出现多个小漩涡,这使得上板面压强大小明显减小,且避免了在光伏板阵列、两侧光伏板上板面底部边缘处出现较大的压强,对整体光伏阵列具有较好的保护作用。
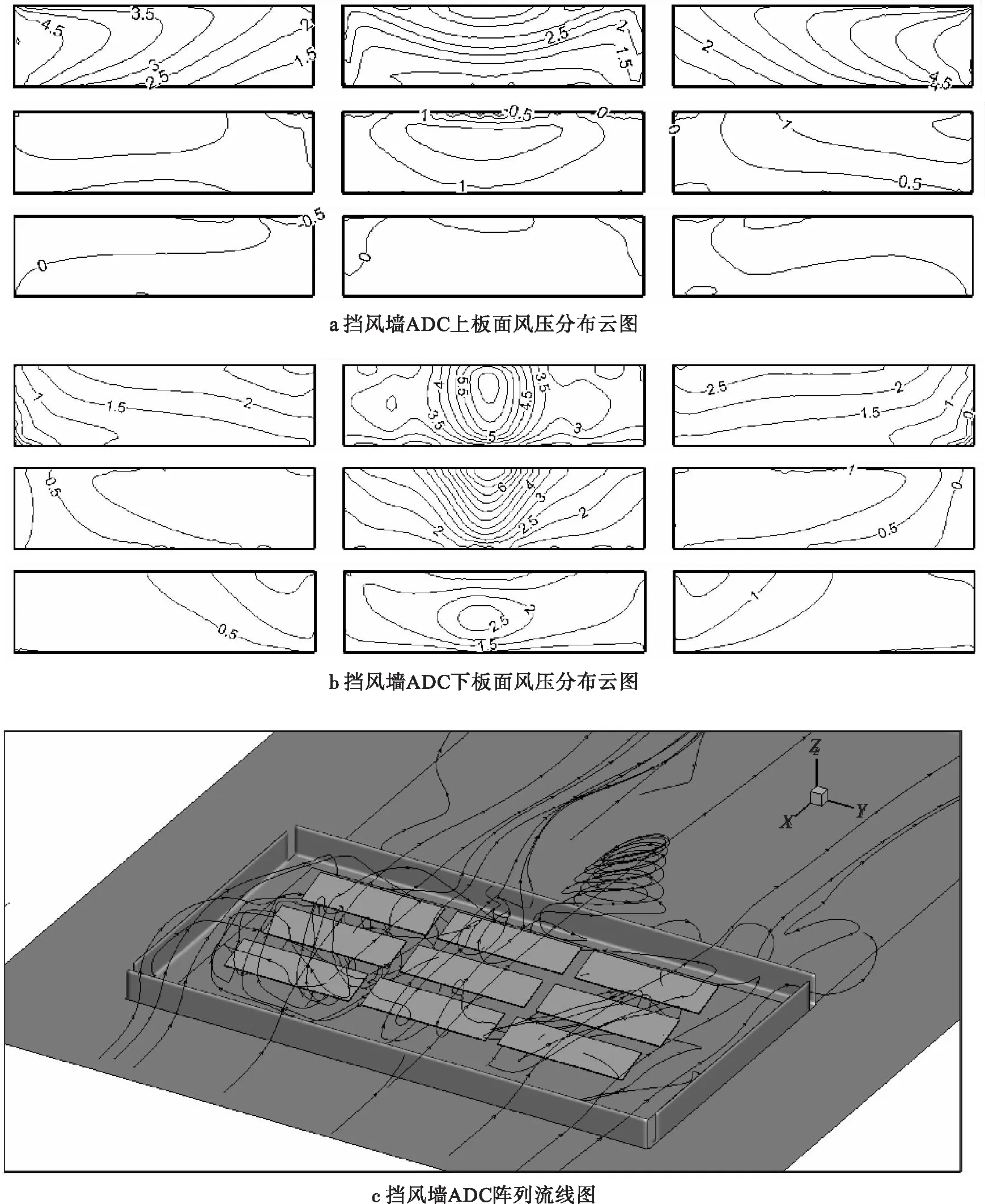
图9 挡风墙ADC光伏阵列板面风压分布云图与阵列截面流线图
5 总结
本文运用CFD数值模拟方法,通过设置不同挡风墙组合,研究光伏阵列板面风压的变化情况,得到如下主要结论:
在0°风向角下,挡风墙不会改变光伏阵列板面风压沿中轴线对称分布的情况。
(1)仅有正面挡风墙A时,第一排光伏阵列板面风压明显减小,但在挡风墙的阻挡作用下,气流回流到第三排光伏阵列,使得第三排光伏阵列风压增大。
(2)挡风墙AC组合,不仅能够对第一排光伏阵列风压起到减缓作用,还能阻挡气流回流到第三排光伏阵列,弥补了仅有挡风墙A的缺陷。
(3)挡风墙AD组合,使得光伏阵列间气流漩涡向光伏阵列顶部移动,使得作用在第一和第二排光伏阵列板面风压大大减小。但并没有限制到气流回流到第三排光伏阵列,这使得第三排光伏阵列板面风压依旧较大。
(4)挡风墙ADC组合,继承了挡风墙A,AD、AC组合的优点,弥补了缺点,对整个光伏阵列起到了风压减缓作用。
