带推力高超声速飞行器非连续点火再入轨迹研究

蔺君， 何英姿， 黄盘兴

(1.北京控制工程研究所， 北京 100190； 2.空间智能控制技术重点实验室， 北京 100190)

0 引言

高超声速飞行器再入包含飞行器控制、制导与规划等方面，是一个高度复杂的综合性问题。再入轨迹规划是分析飞行器再入能力的重要手段，是现代飞行器设计中的重要内容。特别是针对现代随控布局飞行器，轨迹规划影响着总体、气动布局、制导控制、动力和结构等多个分系统的设计。

再入轨迹规划包含直接法和间接法。直接法通过将连续的最优控制问题离散化、参数化，转化为包含优化指标及参数约束的参数优化问题，利用优化方法得到最优解。间接法则基于极值原理和变分法将最优控制变量表示成状态变量和协态变量的函数，将最优轨迹优化问题转化为哈密顿边值问题(HBVP)，通过求解该HBVP，获得相应的最优控制变量和最优轨迹[1]。

间接法求解最优轨迹问题时，协态方程与横截条件等求解过程复杂繁琐，且对初值估计精度要求较高。高超声速飞行器的非线性特性及再入过程的多种约束条件，进一步增加了间接法求解过程的复杂度[2]。无实际物理意义的协态变量加大了初值估计的难度；在含有路径约束时，必须将路径约束转化为终端约束才能解算；含隐式约束条件时，相应的Legendre乘子很难消去，进一步加大了计算量。间接法的这些局限性限制了其应用和发展。直接法根据参数化方法的不同，可分为仅离散控制变量的直接打靶法和同时离散控制变量与状态变量的配点法。单纯离散化和参数化控制输入的直接打靶法对初值较为敏感。直接配点法则同时离散化和参数化控制和状态，为了克服等距离配点易引起“龙格”现象，正交配点法(也称为伪谱法)选取全局插值多项式近似状态量和控制量[3]。

高斯伪谱法(GPM)是Benson在Legendre伪谱法基础上提出的一种改进方法[4]。GPM将状态和控制时间历程在一系列高斯点上离散化，然后用这些离散的状态与控制分别构造Lagrange插值多项式去逼近真实的状态与控制，再通过对状态量求导来代替动力学微分方程，将连续系统最优控制问题转化为受一系列代数约束的参数优化问题。GPM可保证转化得到的非线性规划问题卡罗需- 库恩- 塔克(KKT)条件均与其1阶最优性条件两点边值问题的离散形式完全等价。Huntington对Benson的工作做了进一步扩展，证明了在动力学约束和路径约束同时存在的条件下，用GPM离散得到的非线性规划问题KKT条件仍与HBVP等价[5]。

基于伪谱法的轨迹优化，已在货运飞船返回舱返回轨道设计[6]、火箭上升段轨迹优化[7-8]及在线轨迹优化和再入制导[9]、月球定点着陆[10]、制导炸弹最大射程优化[11]、高超声速飞行器再入轨迹优化[3]以及带有禁飞区[12-14]、航路点约束[15]、总吸热量约束[16]的再入轨迹优化等领域得到应用。为了提高轨迹优化的时效性，火箭返回着陆轨迹优化结合凸优化理论及方法，对推力进行无损松弛，快速得到再入优化轨迹[17]。

然而，针对高超声速飞行器再入轨迹优化这一问题，现阶段研究较多的是针对无动力再入展开。为了提高再入过程飞行器的任务灵活性和机动能力，发展带推力高超声速飞行器，可在再入过程中进行多次点火、熄火，从而改变飞行器再入轨迹和落点。本文针对再入过程中多次点火这一需求，展开带推力高超声速飞行器再入轨迹优化研究。

1 带推力高超声速飞行器再入轨迹规划建模

1.1 带推力再入运动学模型

考虑如下带推力高超声速飞行器再入动力学模型[18]：

(1)

式中：r为地心距；θ为经度；φ为纬度；v为飞行器飞行速度；γ为航迹角；ψ为航向角；T为发动机推力；α为攻角；FD为阻力，FD=ρv2CDSref2，ρ为大气密度，CD为阻力系数，Sref为飞行器参考面积；m为飞行器质量；g为重力加速度；Ω为地球自转角速度；FL为升力，FL=ρv2CLSref2，可通过国际大气数据表查得，CL为升力系数；σ为倾侧角；ce为发动机燃料质量流量。

1.2 再入约束

为了保证飞行器结构安全，飞行器再入过程需要满足如下动压、过载、热流密度等强约束条件：

动压：

Q=ρv2/2≤Qmax,

(2)

过载：

(3)

热流密度：

(4)

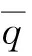
为成功保证飞行任务，飞行器接近任务终端时，需要满足终端约束条件，通常包括如下约束：

终端高度约束：

|hf-h|≤Δh,

(5)

式中：hf为终端高度；h为高度；Δh为高度允许偏差。

终端速度约束：

|vf-v|≤Δv,

(6)

式中：vf为终端速度；Δv为速度允许偏差。

落点位置约束：

|θf-θ|≤Δθ，|φf-φ|≤Δφ,

(7)

式中：θf为终端经度；Δθ为经度允许偏差；φf为终端纬度；Δφ为纬度允许偏差。

飞行器再入过程中需要考虑控制量约束，即

|α|≤αmax，|σ|≤σmax,

(8)

式中：αmax为最大攻角；σmax为最大倾侧角。

带推力再入飞行器还应满足如下发动机工作总时长约束：

(9)

式中：N为发动机点火次数；κν为第ν次点火时长；tz由发动机比冲及推进剂总量决定。

2 再入轨迹优化方法

2.1 高斯伪谱法

考虑如下一般性非线性系统：

(10)

式中：t为时间；x(t)为状态；u(t)为控制输入；t0为初始时间；tf为终端时间。

再入过程应满足的边界条件为

Υ(x(t0),t0,x(tf),tf)=0,

(11)

路径约束为

Γ(x(t),u(t),t)≤0.

(12)

对一般性的Bolza型最优控制性能指标，形如(13)式，

(13)

式中：Φ(x(t0),t0,x(tf),tf)表示初始和终端状态性能指标；G(x(t),u(t),t)表示积分性能指标。

(14)

(11)式可改写为

Υ(x(-1),t0,x(1),tf)=0,

(15)

(12)式可改写为

Γ(x(τ),u(τ),τ)≤0,

(16)

(13)式可改写为

(17)

高斯伪谱法通过选取M阶Legendre-Gauss(LG)点，并以τ0τ(0)=-1为初始节点，在LG点对系统方程进行离散[19]。

(14)式在选取的LG节点可改写为代数约束形式，即

(18)

式中：Dki为微分矩阵，由Legendre多项式递推关系及其导数计算公式迭代计算；X(τk为状态变量x在LG节点τk处的值；U(τk为输入量u在τk处的值；f(X(τk),U(τk);t0,tf)表示(10)式在LG节点τk处的值。

(17)式由高斯积分公式，可近似为

(19)

式中：τf为终端归一化时间；ωk为LG点权值；G(X(τk),U(τk),τk;t0,tf)表示积分性能指标G(x(t),u(t),t)在LG节点τk处的值。

则(14)式在终端时刻可转化为代数约束，即

(20)

同理，(15)式在LG节点离散化后，近似为

Υ(X(τ0),t0,X(τf),tf)=0,

(21)

于是(16)式变为

Γ(X(τk),U(τk),τk;t0,tf)≤0,k=1,2,…,M.

(22)

最终，(14)式～(17)式的解，可通过求解含有多种约束条件(18)式～(22)式的非线性规划来确定。

2.2 分段高斯伪谱法

带推力高超声速飞行器发动机开关机时间对再入轨迹影响显著。发动机的不连续点火将再入轨迹分割成多个阶段，再入轨迹在优化过程中需要考虑分段点处系统状态和控制输入的连接问题。

假设1每次点火时刻为tν，点火推进时长为κν，ν= 1, 2,…,N.

忽略发动机开关机的动态特性，带推力高超声速飞行器再入过程中发动机点火N次，则利用高斯伪谱法进行再入轨迹优化问题被分为2N+1段。若每段包含LG节点数均为K，则分段高斯伪谱法总的配点数为(2N+1)×(K+1)+1. 假设系统动力学方程的维度为n，系统控制输入维度为q，则分段高斯伪谱法总的优化参数量为((2N+1)×(K+1)+1)×(n+q)。

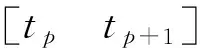
(23)

从而总的性能指标为

(24)

在各个时间区间，路径约束和边界约束为

(25)

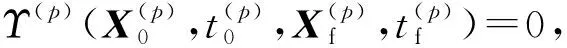
(26)

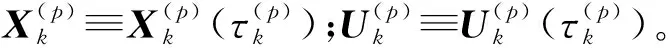
(14)式在离散高斯点转化为如下多段代数方程：

(27)

在各个时间区间内，终端状态约束为

(28)

为了保证各段区间的连续性，系统状态和时间应满足如下条件：

(29)

在各个时间节点，系统控制输入及飞行器质量还应满足如下连续性约束：

(30)

带推力高超声速飞行器采用分段GPM进行再入轨迹优化时，飞行器的控制输入选取为攻角和倾侧角。

在各个时间节点，系统控制输入及飞行器质量还应满足连续性约束。即对于采用火箭发动机在再入段进行推进以增加飞行器机动能力和飞行航程时，推进剂耗尽后，如果本级火箭推进器被抛掉，则此时飞行器总质量应满足：

(31)

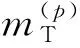
由于飞行器重量及结构限制，再入飞行器多级点火增加飞行器航程及机动能力的方式不能采用过多级的推进器。本文假设飞行器可最多进行2次点火助推，以兼顾性能提升和结构限制。

通过如上数值离散化，带推力高超声速飞行器再入轨迹优化问题即可以转化为分段高斯伪谱法求解目标函数(23)式和(24)式、路径约束(25)式、边界条件约束(26)式、系统动态过程(27)式、终端状态约束(28)式及分段高斯伪谱法连续性约束(29)式、(30)式或(31)式的最优控制问题。

3 仿真校验

以美国波音公司CAV-H高超声速飞行器为例，对再入飞行器无动力再入与带推力再入进行对比。飞行器质量m=907.2 kg，参考面积Sref=0.483 9 m2，Kn=1.65×10-8.

3.1 气动数据建模及攻角剖面

由CAV-H飞行器气动力系数，将其进行近似化处理，阻力系数和升力系数[20-21]可描述为

CD=0.024 67+0.000 714 3α2+0.325 2e-0.279Ma,

(32)

CL=-0.234 2+0.051 36α+0.294 3e-0.100 7Ma，

(33)

式中：Ma为马赫数。

由(32)式和(33)式给出的飞行器阻力系数和升力系数，可得到CAV-H飞行器最大升阻比攻角剖面，如图1所示。

图1 最大升阻比攻角剖面Fig.1 Angle of attack profile for max lift-to-drag ratio

假设CAV-H飞行器再入的初始条件和终端条件如表1所示。

表1 再入初始和终端条件

3.2 无动力再入轨迹规划

选取目标函数为横向航程最大，在选取初始航向角为90°时，最大横向航程可等效为最大纬度，即J=maxφf，φf为终端时刻纬度。在MATLAB软件仿真环境下，利用GPM进行轨迹规划，无动力再入过程优化变量为攻角和倾侧角。采用文献[20]中的方法，得到无动力再入轨迹。

仿真结果表明，再入轨迹的最大横向航程可达48.136 7°，约为5 358.4 km，纵向航程可达50.690 5°，约为5 642.7 km. 高超声速飞行器再入轨迹，包括高度、速度、航迹倾斜角、航迹方位角、终端条件均可满足，且再入攻角和倾侧角均位于控制输入边界以内；动压、过载、热流密度均小于允许的最大值。无动力再入时，高超声速飞行器再入轨迹较平滑。

3.3 再入点火时刻点火时长分析

在无动力再入轨迹优化基础上，分别在不同时刻施加发动机推力，并考虑再入过程路径约束和边界约束，研究发动机点火时刻以及点火助推时长对再入飞行器估计的影响。选取如图2所示A、B、C、D共4个时刻，分别对应再入初始时刻A、再入过程中度过最大热流密度时刻后，飞行器高度再次达到最高点时刻C、点火时刻A和点火时刻C对应中间高度时刻B，此时飞行器处于接近最大下降速度以及将近飞行器接近半程航程时刻D.

3.3.1 再入点火时刻分析

假设2发动机空质量为18 kg，推力为10 kN，发动机比冲Isp为260 s，助推时间为20 s.

发动机点火后，一次性充分燃烧推进剂，完成助推。由ce=T/(Ispg0)(g0为海平面重力加速度)可知，质量流量为3.925 2 kg/s. 由假设2可知，推进剂总质量为78.5 kg.

图2 带推力再入点火时刻Fig.2 Ignition timing of powered reentry

带推力飞行器再入初始质量为1 003.7 kg，采取与无动力再入相同的初始条件(见表1)及约束条件，在给定A、B、C、D4个时刻分别进行点火助推。带推力飞行器达到终端时刻质量为飞行器质量与发动机空质量之和，为925.2 kg. 带推力再入与无动力再入终端状态如表2所示。

图3所示为点火时刻助推轨迹。由图3可见，发动机点火助推可满足再入轨迹对终端状态的约束包括速度和高度要求。飞行器在再入初期维持大攻角，飞行器气动力达到一定临界值后，飞行器转入最大升阻比攻角飞行器，以获得最大的飞行航程和侧向航程。由图3(a)可见，发动机在时刻A和时刻B点火后，飞行器再入轨迹变化不大，基本与再入无动力轨迹类似，但飞行时间、横程、纵程较无动力明显增大。在点火时刻C和时刻D点火后，飞行器轨迹出现小幅波动。飞行器在到达时刻C之前，气动力已经产生明显作用，通过点火增加飞行器速度后，为了满足飞行器终端约束保证速度和高度要求，再入轨迹需要进行多次调整，导致轨迹出现一定波动。

表2 不同点火时刻助推及无动力再入终端状态对比

由图3仿真结果可知，带推力高超声速飞行器可大幅提高飞行器再入射程。发动机点火时间越早，飞行器射程增加越大，但飞行器飞行时间也越长，导致飞行器总的吸热量增加。飞行器在时刻A和时刻B点火需要进行攻角和倾侧角的双重调整，从大攻角调整至11°左右的最大升阻比攻角，倾侧角调整至0°，需要利用飞行器姿控发动机进行调姿，能量消耗较大。在时刻C和时刻D点火仅需要利用飞行器气动力进行操控，能量损耗小。

3.3.2 再入点火时长分析

在图2所示的4个时刻火点，分别施加不同推力大小、不同助推时长的再入点火助推形式，对飞行器最终状态进行对比，如表3所示。

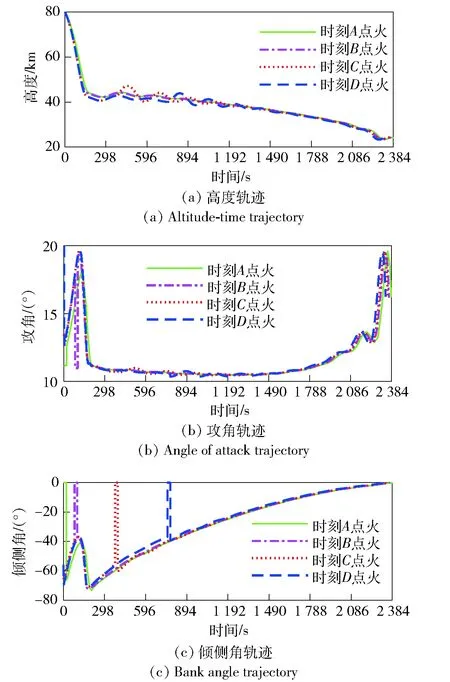
图3 不同点火时刻助推轨迹Fig.3 Powered reentry trajectories at different ignition times

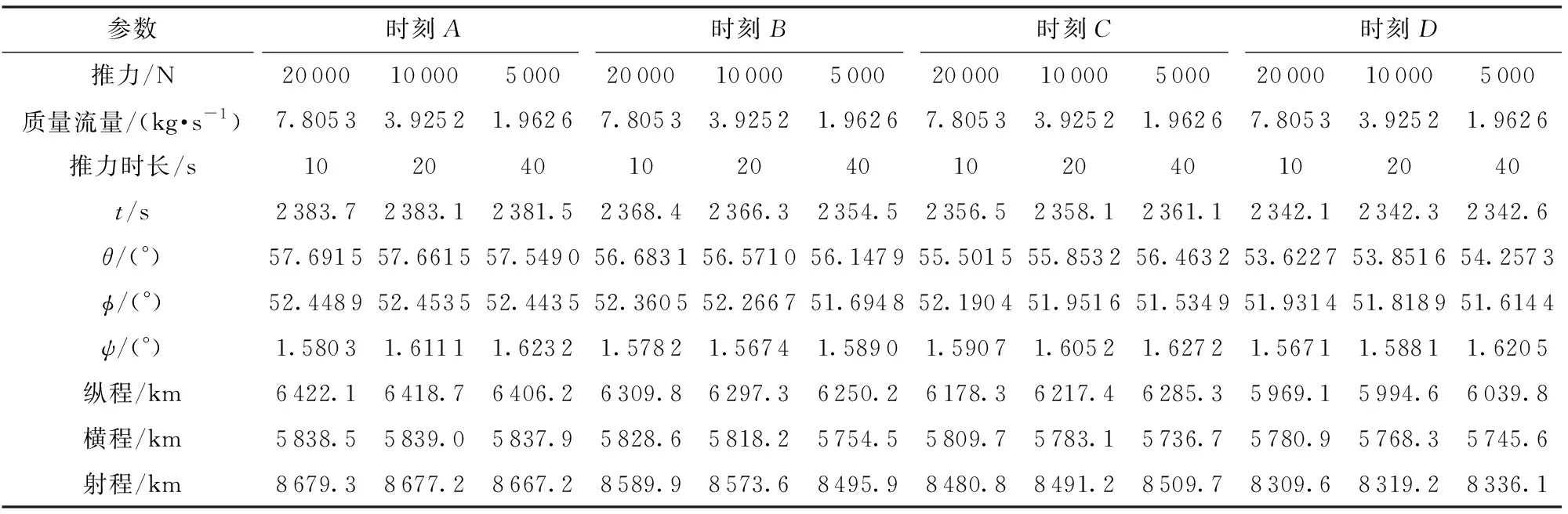
表3 不同点火助推时长终端状态对比

由表3可知：在再入初始时刻A施加不同时长的助推，相当于改变再入初始速度，对飞行器总的飞行时间有影响，但改变较小；在时刻B点火，由于飞行器气动能力不足，难以保持平衡滑翔姿态，点火助推加剧飞行器下降速度，导致再入飞行时间变短；在时刻C和时刻D，升力已足够维持飞行器平衡滑翔，点火后，飞行时间均有小幅增长。由此也可推断，在时刻C之后点火助推，飞行器飞行时间较无动力时，均会增加，且助推时间越长，总飞行时间也相应增加。在4个时刻点火，当总冲一定时，飞行器终端状态变化不大。即大推力短时间助推和小推力长时间助推，在选取最大横向航程的目标函数下，对飞行器终端改变基本一致。

3.4 带推力再入轨迹规划

为了进一步说明发动机推力在不同点火时刻的作用，将发动机推力分为两次进行点火助推，分别在时刻C和时刻D进行增程助推设计。

假设3再入过程中发动机可进行两次点火，即p=2，且点火时长均为10 s.

带推力高超声速飞行器的再入初始状态和终端状态与无动力再入时相同(见表1)，目标函数为横向跨度最大。根据假设3，完整的再入轨迹分为5段，飞行器质量为

再入过程中发动机点火时，攻角维持在最大升阻比攻角，倾侧角维持在0°. 采用分段高斯伪谱法和数值积分对带推力高超声速飞行器进行再入轨迹优化后，得到再入轨迹如图4所示。

由地面经纬图4(a)显示，带推力再入轨迹的最大横向航程可达51.754 8°，约为5 761.2 km，纵向航程可达54.054 0°，约为6 017.1 km，飞行器射程为8 330.5 km. 高超声速飞行器再入轨迹如图4(b)～图4(e)所示，包括高度、速度、航迹倾斜角、航迹方位角，且均满足终端约束条件。再入攻角和倾侧角如图4(f)～图4(g)所示，再入攻角和倾侧角均位于控制输入边界以内，在分段点处对发动机进行两次点火，分别产生推力，使飞行器速度增加，再入攻角和倾侧角对应当前环境的最大升阻比攻角和0°倾侧角。动压、过载、热流密度如图4(h)～图4(j)均小于允许的最大值。由图4(k)带推力再入三维轨迹可见，高超声速飞行器可平稳滑翔飞行。带推力高超声速飞行器质量变化如图4(l)所示。

图5所示为高超声速飞行器带推力与无动力再入轨迹对比。由图5可见：高超声速飞行器带推力较无动力再入时，经度增大约为3.363 5°，纬度增大3.618 1°，飞行距离增加约为549.907 7 km；再入过程中由于发动机两次点火以及倾侧角保持在0°，再入轨迹较无动力时，呈现一定的波动。

3.5 关于发动机点火时刻攻角和倾侧角的讨论

图6所示为高超声速飞行器不同点火时刻助推与无动力再入攻角对比。由图6可见，在点火时刻C和D，攻角基本维持在最大升阻比攻角，因此将点火后助推段的攻角剖面选择为最大升阻比攻角[22]。倾侧角维持在0°，以保持飞行器升力仅存在于飞行航迹方向，从而尽量拉升飞行器，以取得最大的航程。

图4 分段GPM带推力再入轨迹优化Fig.4 Powered reentry trajectory optimization using MGPM

图5 带推力与无动力三维再入轨迹对比Fig.5 Comparison of 3D powered and unpowered reentry trajectories

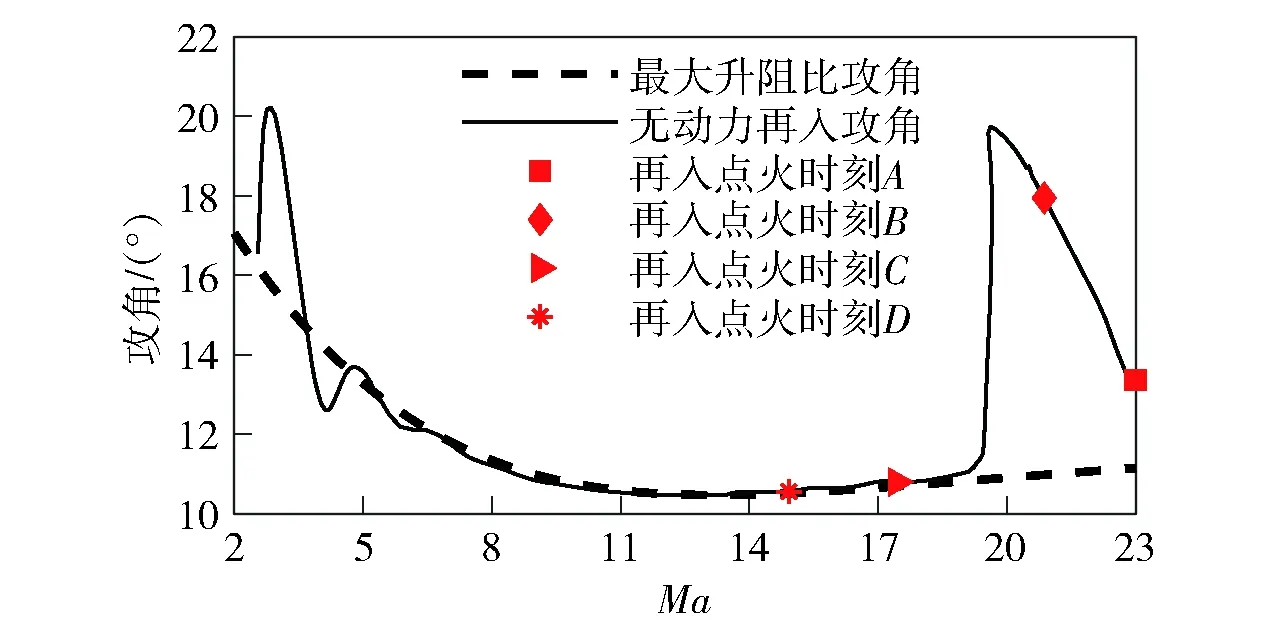
图6 不同点火时刻助推与无动力再入攻角对比Fig.6 Comparison of angles of attack at different ignition times during powered and unpowered reentries

3.6 标称轨迹下飞行器制导终端状态

利用高斯伪谱法得到的飞行器再入攻角和倾侧角指令后，飞行器利用数值积分方法可得到在标称轨迹下的飞行器飞行轨迹。表4所示为跟踪标称轨迹终端状态对比。由表4可见，带推力高超声速飞行器可较好地实现对标称轨迹的跟踪，飞行器终端状态误差很小。

表4 跟踪标称轨迹终端状态对比

4 结论

本文给出基于分段GPM和数值积分对带推力高超声速飞行器非连续点火再入轨迹进行优化。优化求解到的轨迹满足分段GPM连续性约束及过载、动压、热流密度约束。分段GPM方法将再入轨迹在发动机点火时刻进行分段，发动机关机时利用分段GPM进行轨迹优化，发动机开机后利用数值积分，计算再入轨迹。

数值算例结果显示，分段GPM和数值积分可以有效生成满足连续性约束及常规约束的再入轨迹，在总冲一定时，发动机点火时刻对再入轨迹影响明显。高超声速飞行器两次点火产生的速度增量可有效增加飞行器的纵向航程和横向航程，并有效提高飞行器再入机动能力和灵活性；分段GPM规划得到的控制输入可作为参考标称轨迹指令，辅助制导系统设计。