基于矢量路面提取道路中心线智能提取方法的实现

刘学民

0 引言

在地理信息数据中，道路网络是构成几何数据和应用分析的重要组成部分，道路网的描述，是用GIS 方法对自然界中人文影响和经济状况的表现形式。对于道路网数据采集，往往是采用人工采集和计算机辅助自动化采集两种方法。在许多GIS 平台，道路面提取中心线的原理有下面两类方法：（1）道路面按Delaunay 方法构造三角网，此方法在对路端喇叭形处生成的中心线表现为波浪折线和不正确的分叉，点数也较多，与理想形状的边线点几何形似差异较大。（2）提取道路的面填充，生成栅格位图。这种方法除了数据格式转换烦琐，还有矢量数据属性的丢失。本文将针对以上情况，对路面形状进行边线调整、路端处理后，依据科学的计算判别，在已有软件中二次开发自己的工具实现道路中心线自动提取的功能。

1 提取中心线算法原理

对道路面的边线点，按某种算法找到道路的两端封口线，从一封口中点起，沿道路一侧点顺序，根据道路边线点的相互关系，逐点查找顺序点的路边线另一侧对称点，将该点与对称点连线并取中点作为待求中心线新加点。当此点不存在时，求该点内角平分线与道路另一侧最近的实交点，将该点与求得的交点连线，取中点作为待求中心线新加点，直至道路另一封口中点为止。需要对道路面进行结构分析，找出其点坐标与这些特征的关系即相关性。

2 道路封口的确定

2.1 没有交叉口单一路面封口的确定（见图1）

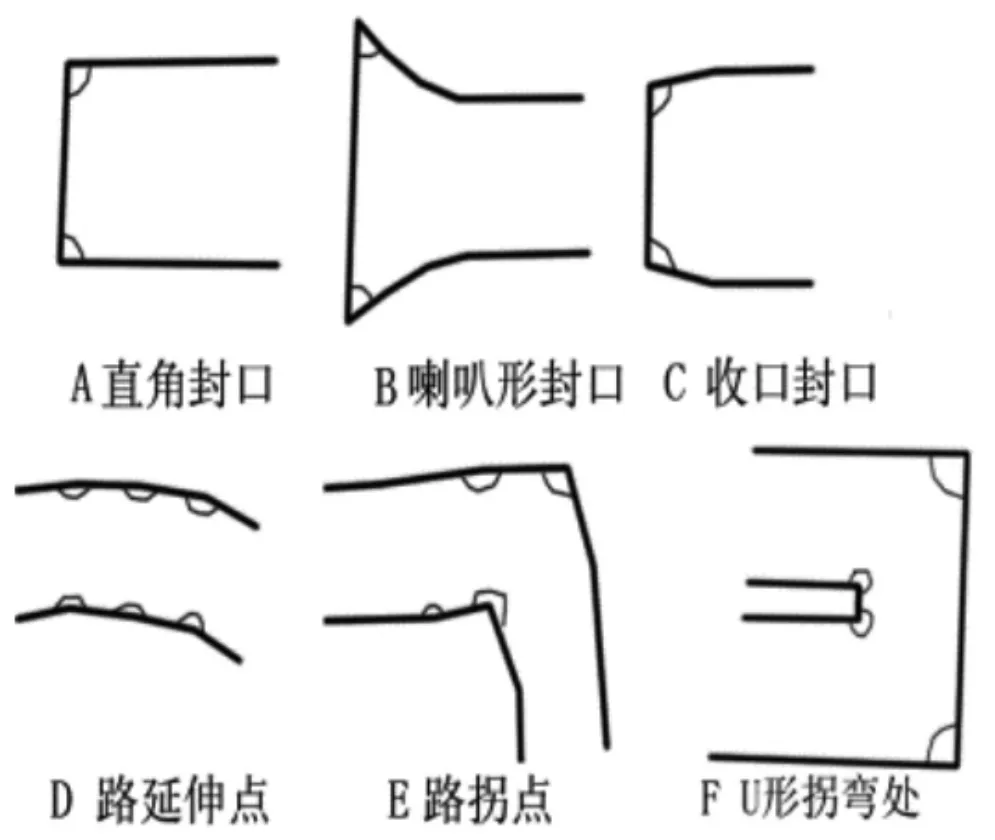
图1 路面夹角与边线关系

在确定是否封口前，首先求出道路面的所有点对应的内角值，道路面经作业人员整理后，路的端口线段两顶点夹角基本对称，或接近成直角（如图A）或呈张口喇叭状（如图B），对于收口形的（如图C）基本没有。在道路面其他非端口处的各线段，当路正常延伸时，都是远大于90 度的拐角（如图D），当有近90或小于90 度的角时，该段线如果不是封口，则另一点的内角一定与本点内角严重不相近，此时该点是道路的拐弯处（如图E），相反，如果该线段两端的内角出现了接近90 度及以下并且两角接近，那么该段线一定是封口。对于U 形路（如图F），假如U 形底处是一段直线段，此时该处内侧和外侧两线段的顶角也是角对称的，在U 形内侧边线两顶角，接近270 度，自然不会判断为封口，在U 形外侧边线两顶角，都接近90 度，但是，此线段的长度会远大于道路的平均宽度，至少在两倍以上，否则无法构成U 形路面，按接近90 对称角再加上此边的边长与平均路宽的对比条件，可以进行排除。经作业员整理后的一条道路面，原则上只有两端两个封口，这使得此法识别封口正确性达到了百分之百。

2.2 含有交叉口路面的分割与封口的确定

对于路面交叉没有断开的情况，路面可能存在多个十字路口或丁字路口，为了按2.1 中确定单一路面封口两端，必须对路面进行分割，分割可以在工具中实现，自动分割方法如下:

（1）写工具时，取消只找到两个封口的限制，对发现的可能封口全部侦测并记录。

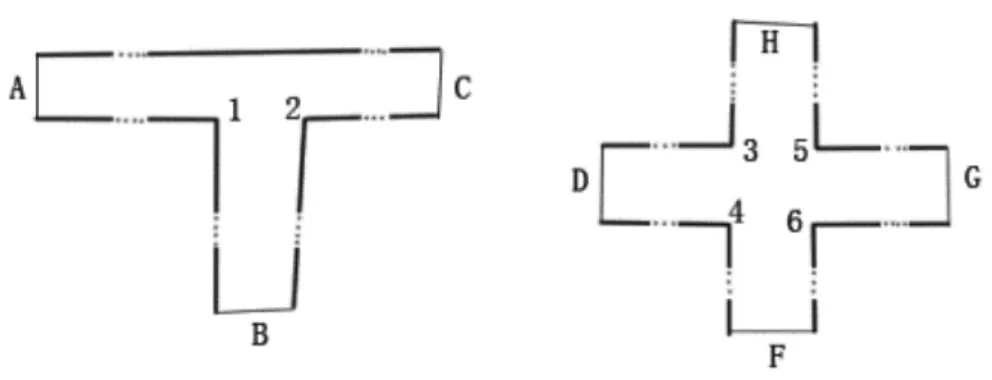
图2 交叉路口和丁字路口未断开情况示意

（2）交叉口判别，对有三个及其以上侦测封口的路面按每个侦测的封口分别沿其两侧边线逐点延长寻找，各自搜索一对两内角都近似270 并且连线距离与平均路宽接近的点，此两点即为交叉口处，将此两点作为该路面的一个结束封口，然后与出发的封口之间的点划分为一段路面。距离比较时，一定是两侧分别找到的270 度拐点之间，如图中丁字路口中，从A 封口上边线搜到2 号点与沿下边线搜到的1 号点可作为交叉口，若从C 封口开始得一样结果。若从B 封口也可搜到1 点和2 点。对于图中的十字路口，从侦测到的四个封口任意一个开始，都会搜索到符合该条件的 3 点和 5 点、5 点和 6 点、6 点和 4 点，4点和3 点其中一个，逐次分割路口。

（3）对某路面上新划分出的路段面从原面上分割下来。如图中丁字路口，沿A 封口找到1、2 号点后，分割出上面的横向路，同时还有下面的竖条路段。对于十字路口，则需要分割两次。

（4）在分割剩余的面上继续执行交叉口判别、分割操作，直到所剩封口数为不多于2 个时为止。

3 确定路连续点序边线作为搜索边

当路封口确定后，加在两封口之间的各点，构成了道路的两条边线。在这两条边线中，有一条是包含起止点即面的闭合点，另一侧不包含此点，而是顺序点号连续的系列线段。为了提取中心线时从一封口向另一封口连续进行，需要找到该点序连续的边线。如果对道路面从开始到闭合将各点依次编号，这些编号值有下面特征：利用道路两封口的端点编号计算，最大号与最小号之间包含的线段包含闭合点，中间点号不是连续的，而另一侧中间点号是连续的。本方法中心线搜索推进按点号连续一侧执行，同时，还要确定对面边的点序，在闭合点小号一侧，点号从大到小，闭合点大号一侧，是从小到大。

4 确定道路的路宽和平均路宽

在正常生产中，经作业员对道路调整后，同一路段的宽度是基本对称和均匀的，对道路面内角180±10 度即平角的点在角分线方向求取内割线的长度为当前点的路宽。确定该点路宽时，应排除该割线与封口线相交的情形。该条路所有符合条件的路宽值取平均值，可作为道路的平均宽度。

5 确定道路弦线

将近似垂直于中心线的割于道路两边线之间的线段称为弦线，弦线中点可作为求道路中心线的依据。确定最佳弦线是求得最佳道路中心线的中心思想。道路面经人工调整后，道路两侧边线往往具有明显的对称特征，其情况如图3 中作为对应的点应同时满足以下角度和距离条件。

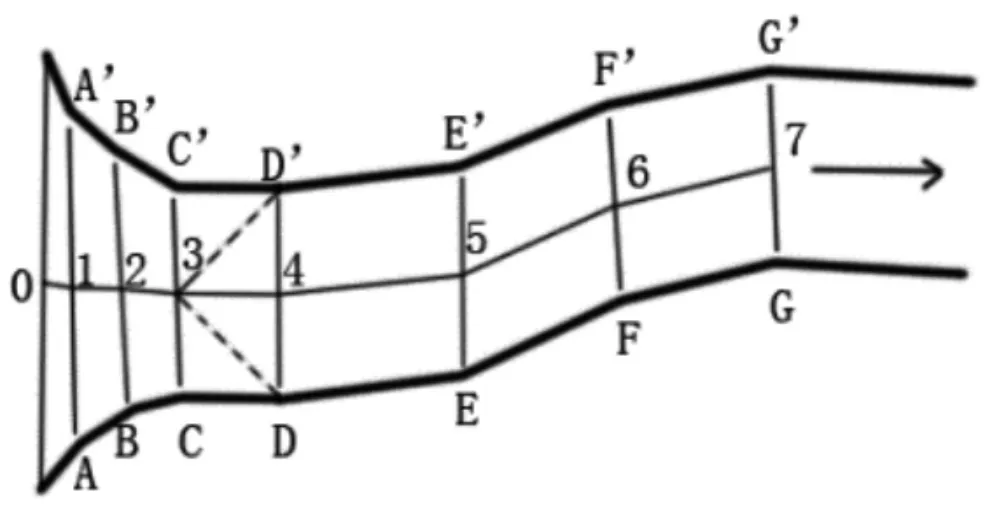
图3 道路对称点示意

（1）角度相关：（1）对称点处的内角与180 差值绝对值近似相等，且两个内角和接近 360 度；图中的 D 与 D’、E 与 E’、F 与F’、G 与 G’等处。（2）两个角均大于 180 度，此时是喇叭拐弯处；图中的 A 与 A’、B 与 B’、C 与 C’。

（2）距离相关：道路中两对称点距前一个弦线中心点的距离应近似相等如图中的D 和D’到3 点的距离近似相等。设定一个范围值，该值大小与构成对称点的对称程度相关，取决于人的作业特点；与道路宽度没有直接比例关系，但路宽度大时也应略大。本例取0.2 倍路宽，道路较宽时，比例数可适当减小。

以上满足条件的点，确定为对称点。当对面点细密时，一个本侧点可能会连续找到几个对面点都满足对称条件，此时放弃寻找对称点，采用角平分线法确定中心线点。对于找到的对面对称点，记录其已成为对称点的状态并记录两点连线为弦线，在后续查找时，搜索对称点时，应在前面所使用过的点开始向后查找，所得的新对称点间连线与前面使用的弦线均无除两端外其他实交点，防止中心线回折和交叉。当顺序点没有找到对称点时，使用该顺序点的内角平分线，求与另一侧的交点并以该交点与本点的连线作为弦线。利用对称点作为提取中心线，可以最大限度地保持中心线与原道路的形状相似。

6 结论

本方法通过实际运行，得到的中心线正确，速度快。本方法克服了一些软件提取道路中心线的波浪小折线、分叉、点数大量冗余以及运算复杂的弊端，所生成的中心线与原边线形状完美一致。在编辑软件中使用，能保证道路属性内容保留完整，直接传递。由于计算方法简单，运算速度也较快，适用于各种语言编写工具。