基于改进双种群混合遗传算法的车辆路径问题研究

何国强 李斌成 王东先

摘 要：针对传统遗传算法求解带容量约束的车辆路径问题，存在早熟收敛、易陷入局部最优等问题，设计了双种群混合遗传算法。种群I在传统遗传算法中引入模拟退火思想及变邻域搜索策略，增强算法局部搜索性能。种群II在迭代过程中，通过设定阈值判断当种群达到早熟收敛状态时，利用“移民策略”植入外部个体，达到增加种群多样性、增强算法全局搜索和开发的能力。每次迭代完成后采用“移民算子”进行种群间的信息交流。最近邻插入方法在算法迭代结束之后对求解所得最好解的各子路径进行再优化。算例验证分析可知，所提算法计算结果同算例给出的最好解之间的偏差均在-1.00%以内，求解质量优于所有对比的算法，表明所提算法能有效解决容量约束的车辆路径问题，具有可靠的全局稳定性。

关 键 词：容量车辆路径问题;双种群;混合遗传算法; 移民策略;局部搜索/全局搜索

中图分类号：TP301.6  文献标志码： A 文章编号：2096-7934（2020）07-0108-11

一、 引言

车辆路径问题（vehicle routing problem， VRP）是典型的组合优化问题，经过不断发展，在VRP问题的基础上衍生出了很多其他问题，如：带时间窗的VRP（vehicle routing problem with times windows， VRPTW）、多配送中心VRP（multiple depot vehicle routing problem， m-VRP）、容量限制的VRP（capacitated vehicle routing problem， CVRP）等。其中，容量限制的VRP（capacitated vehicle routing problem， CVRP）实用性较为广泛，因而吸引了众多学者进行研究。目前，关于CVRP的计算方法主要分三类：精确算法、启发式算法及智能优化算法。精确算法与启发式算法对于较大规模CVRP问题求解比较困难，因而，目前对CVRP问题求解方法的研究主要集中在智能优化算法上，如遗传算法（GA）[1]、模拟退火算法（SA）[2]、蟻群算法（ACO）[3]。石兆[4]通过对智能优化算法求解CVRP问题研究发现，禁忌搜索算法求解时间较短，但求解效果不稳定，禁忌规则也不易确定;模拟退火算法在牺牲时间的前提下可以计算得到相对满意的结果，但存在易陷入局部最优的缺陷;蚁群算法存在求解效率低，容易产生早熟收敛现象的缺陷。考虑到以上智能优化算法的缺点和不足，近年来，有学者提出了这些算法的改进方法，如将多种智能算法融合以及设计新的算法。

采用多种智能优化算法混合来求解CVRP问题的研究主要有：刘万锋等[5]通过引入四种局部搜索算子进行了解的合法性评估，提出利用快速多邻域迭代局部搜索算法（fast multi-neighborhood ILS， FMNILS）求解车辆路径问题，该算法在计算时间及解的满意程度等方面都表现良好。王文蕊等[6]研究了带诸多实际约束的大规模车辆路径问题，按照地理区域的不同对客户进行划分，通过改进K均值聚类法对各区域配送线路进行聚类分析，从而将问题转化为小规模的旅行商问题，但该方法对于多阶段优化算法中的K均值聚类中心点的选择方法仍需改进。姜婷[7]提出了混合差分蜂群算法，通过采用全局最优解指导邻域搜索策略来增强人工蜂群开发能力不足的缺点，并通过差分算法的交叉更新策略对所提出的算法进行局部优化，该算法缺点是求解稳定性较弱。毕志升等[8]提出了基于Pareto支配接受准则的多目标模拟退火算法，但所设计的搜索策略对多目标搜索具有偏向性，因此仍需设计更好的局部搜索策略来避免搜索策略对多目标的偏向性问题。陈亮[9]通过对传统蚁群算法计算结果质量差、收敛性弱等缺点的研究，提出了一种改进的蚁群算法来求解CVRP问题，通过引入基于DT策略的候选集来改进构建路径质量，且在迭代过程中加入GIIM算子增强了局部搜索能力，但相比于其他类似算法，并不具有很大优势，甚至很多结果都劣于类似算法的求解结果。

新设计算法求解CVRP问题的研究主要有：蒋海青等[10]提出通过化学优化算法求解CVRP问题，借鉴遗传算法交叉和变异算子设计了分子的相撞、拆解、撞墙及局部优化的合成等四种反应来实现解的改进，并利用动态变化方式对相关参数进行控制，提高了算法的求解效率及全局搜索能力。颜腾威等[11]研究了和声搜索算法在求解CVRP问题时存在搜索能力弱等缺陷，提出改进的和声搜索算法，通过改进和声音调生成策略及利用2-opt算子对新生成的和声进行优化，既约束了不可行解的产生、压缩搜索空间，又提升了搜索效率，但算例求解结果均劣于遗传算法等经典算法。周和平等[12]针对传统蚁群算法计算CVRP问题时的不足，提出了一种改进的蚁群算法，改进的算法在求解速度以及解的质量方面都有很好提升。李阳等[13]设计了一种变邻域生物共栖算法，采用三种共栖搜索算子，提高了算法全局搜索能力，该算法具有较好的全局稳定性。夏茂庚等[14]通过研究节约里程算法和蒙特卡洛模拟方法，将二者特性相结合提出了Flag-MCS-CWS算法，为车辆路径问题的求解提供了很有效的方法，该算法只对算例中30个点以内的问题进行了验证。

上述文献在求解CVRP问题时，其有效性和优越性均得到了验证，但也存在因父代的不合法使得算法搜索范围受限等问题，上述文献中所采用的验证算例多以小规模问题为主，对较大规模问题的求解是否有效还有待进一步考证。在求解CVRP问题的智能优化算法中，遗传算法作为最传统、最经典的优化算法，最适合CVRP问题的求解。因此，本文在程子安等[15]算法的基础上设计了双种群混合遗传算法（double population hybrid genetic algorithm， DPHGA ）来求解CVRP问题，期望在求解精度上有较大程度提升。

二、 车辆路径问题数学模型

其中：（1）式表示目标函数;（2）式表示每辆车载重约束;（3）式表示每个客户都被服务;（4）—（5）式表示保证每个客户只被一辆车服务;（6）式表示消除子回路;（7）—（8）式表示二元变量取值范围。

三、 双种群混合遗传算法

研究发现，传统遗传算法在求解CVRP问题时，随着迭代次数的递增，种群多样性降低，初始种群产生的随机性对解的影响巨大，造成了算法在寻优过程中存在早熟、收敛、陷入局部最优等问题。因此，文章考虑设计双种群混合遗传算法来提高算法的优化性能，种群I作为精英群体进行局部搜索，种群II作为劣势群体进行全局开发。其中，种群I结合模拟退火算法思想及变邻域搜索策略进行邻域搜索，提高局部搜索性能;种群II采用传统遗传算法，对劣势群体进行移民操作，增强全局开发能力，同时在进化过程中将种群I中最差个体同种群II中最优个体进行交换来实现两个种群的协同优化，从而提高算法计算结果的稳定性，降低计算结果的波动性。

（一）算法设计

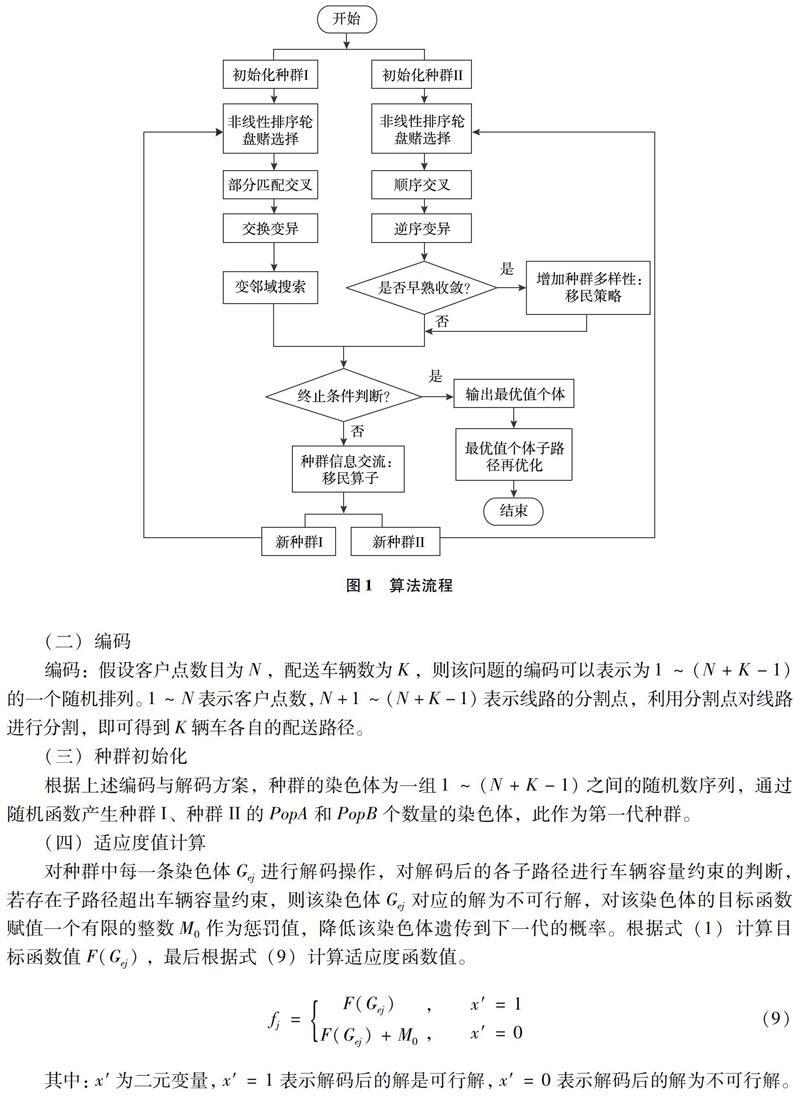
DPHGA算法求解车辆问题的流程如图1所示，种群I着重算法的局部搜索能力，种群II着重算法的全局搜索能力。

（二）编码

编码：假设客户点数目为N，配送车辆数为K，则该问题的编码可以表示为1～（N+K-1）的一个随机排列。1～N表示客户点数，N+1～（N+K-1）表示线路的分割点，利用分割点对线路进行分割，即可得到K辆车各自的配送路径。

（三）种群初始化

根据上述编码与解码方案，种群的染色体为一组1～（N+K-1）之间的随机数序列，通过随机函数产生种群I、种群II的PopA和PopB个数量的染色体，此作为第一代种群。

（四）适应度值计算

对种群中每一条染色体Gej进行解码操作，对解码后的各子路径进行车辆容量约束的判断，若存在子路径超出车辆容量约束，则该染色体Gej对应的解为不可行解，对该染色体的目标函数赋值一个有限的整数M0作为惩罚值，降低该染色体遗传到下一代的概率。根据式（1）计算目标函数值F（Gej），最后根据式（9）计算适应度函数值。

（五）遗传算子

1. 选择算子

文中选择算子采用沈斌等[16]提出的具有良好鲁棒性的非线性排序轮盘赌策略，可以克服算法过早收敛。将两种群的各自的染色体适应度值从小到大进行排序，并按式（10）分配概率。

2. 交叉算子

所谓交叉运算，是指对两个相互配对的染色体根据交叉概率按某种规则相互交换其部分基因，从而形成两个新的个体。交叉运算在遗传算法中起关键作用，是产生新个体的主要方法，在一定程度上影响着种群的多样性，为了提高搜索性能，对双种群采用不同的交叉策略，记两个种群分别为种群I和种群II。

（1）种群I交叉算子：采用部分匹配交叉算子（PMX），该交叉操作的对象是连续基因片段，基本思想源于一维线性结构的基因位置顺序，PMX操作生成新的子代个体，这些子代个体继承父代或生成新的连续优良基因的可能性较高。

（2）种群II交叉算子：采用顺序交叉策略（OX），同部分匹配交叉策略基本相同，唯一不同點是以父代中选择的基因片段为操作对象进行。

3. 变异算子

变异是指根据变异概率将个体编码串中的某些基因值用其它基因值来替换，从而形成一个新的个体。遗传算法中的变异运算是产生新个体的辅助方法，它决定了遗传算法的局部搜索能力，同时保持种群的多样性遗传算法中的变异运算是产生新个体的辅助方法，它决定了遗传算法的局部搜索能力，同时保持种群的多样性。

（1）种群I变异算子：采用两点交换变异策略，通过随机的方式，在个体任意相邻两分隔符之间选择两个不同位置的基因，将它们的基因进行交换。

（2）种群II变异算子：采用逆序变异策略，通过随机的方式，在染色体的编码序列中选择两个不同基因座之间的基因，将其逆序排列，生成一个新的编码序列。

（六）种群I局部搜索策略

种群I完成变异操作之后，对其进行变邻域搜索策略，来提高种群在进化过程中的多样性，增强算法局部探索能力，进一步提高算法搜索到满意解的概率。

1. 抖动操作

“抖动”是邻域生成的主要方法，通常采用以下三种策略进行：互换操作（swap），随机交换染色体某两个基因的位置;逆序操作（reversion），将染色体某两个基因位置之间的基因序列逆序; 插值操作（insertion），随机选择一个基因位置将其插入染色体其他位置。为了使算法能够对这三种邻域进行合理搜索，避免不必要的计算，采用易军等[17]提出的概率策略进行选择，定义在开始邻域搜索之前种群I中每个个体i适应度值为f（i）。

Step1：对三种邻域分别进行k次搜索，找出在第t种邻域下的个体最优适应度值f′（i，t），按照式（12），（13）计算第t种邻域下的奖励值η（i，t）。

Step2：按照式（14）计算各邻域的概率，利用轮盘赌选择需要搜索的邻域，一次搜索完成后即更新奖励值。

2.Metropolis 接受准则

对种群I中染色体产生的新邻域进行判断，具体步骤如下。

Step6：若满足终止条件，则更新当前最优解，结束程序;否则按照衰减函数衰减T后返回Step2。以Metropolis链长L为终止条件。

Step7：种群I所有个体完成邻域选择操作以后，更新当前最优解，并将变异完成后产生的种群与经过局部搜索策略产生的新的种群进行合并，按照目标函数值从小到大进行排序，从中选出种群I中染色体数目的个体作为下一次进化的种群。

（七）种群II移民策略

随着遗传算法迭代次数的增加，种群逐渐收敛于最适应环境的个体，种群多样性随之降低，种群群体结构趋于相似，从而降低了搜索效率，算法也会随之产生早熟收敛现象，可见改善种群多样性是解决早熟收敛问题的主要方法。因此，在算法进化的过程中，通过采用张义长等[18]“移民策略”对种群II引入外部个体，替换部分适应度值较小的个体，以此打乱群体结构来增加种群多样性，从而进一步增强种群II的全局开发以及搜索能力。

由于种群多样性的减少主要体现在群体间个体适应度值的接近程度上，即种群适应度值方差的减小，为了简化计算，利用公式（15）计算适应度方差，当E小于某一阈值时，可认为算法存在早熟收敛现象，可对其进行“移民策略”操作，阈值的取值通过算例测算后获得。

（八）种群间信息交换

双种群遗传算法，在进化过程中，各种群之间是相互独立的，不同种群之间通过“移民算子”[19]实现信息交流。移民算子将两个种群在进化过程中求得的特定个体定期引入到对方的种群中，保证种群I中精英群体进行局部搜索，种群II中劣势群体进行全局开发，从而实现种群间的信息交流和协同进化。具体流程为：用种群II中的最优个体同种群I中的最差个体进行交换。

（九）局部再优化

通常，求解CVRP问题所得结果均须采取其他措施进一步优化。文中采用最近邻插入方法[20]对求解所得最好解的各个子路径进行再优化，以此寻找比当前更优的解。最近邻插入方法是一种改进的局部搜索算法，通过反转每条子路径来实现结果的优化，对进化完成后生成的最好解对应的各子路径进行顺序调整。

最近邻插入法流程如下。

Step1：取配送中心0点为线路的起始点;

Step2：在所求得的子路径中寻找客户点l，使得c0l值最小，从而构成该子路径中的一条局部线路0-l-0;

Step3：从所求得的子路径客户点中，寻找不属于Step2中局部线路的客户点并离该局部线路最近的k点;

Step4：在局部线路上寻找使得cik+ckj-cij最小的弧线（i，j），将点k插入到（i，j）之间;

Step5：重复Step2～Step4，直到该子路径上所有客户都被访问为止;

Step6：重复Step1-Step5，直到所有子路径均优化完成为止。

四、 算例验证及结果分析

本文选取CVRP问题测试集中的SetA、SetB、SetP部分算例对DPHGA进行测试。实验环境为CPU：2.50GHz;开发环境：Matlab R2015b;在Intel（R） Core（TM） i5-2450M CPU@2.5GHZ、4GB RAM计算机和windows7平台上运行。算例参数设置为：种群I、种群II的规模NP根据所求算例规模进行动态调整;客户规模在30～50之间时，种群NP=50，迭代次数为MaxGen=1000，客户规模在51～80之间时，种群NP=80，迭代次数为MaxGen=2000;种群I交叉概率PcA=0.9，种群I变异概率PmA=0.1;种群II交叉概率PcB=0.9，种群II变异概率PmB=0.1;模擬退火变邻域选择策略初始温度t0=10，温度退化率ρ=0.99，Metropolis链长L=10;早熟收敛判断阈值经测算，取值为E=1.0e-14，不满足约束个体的适应度函数惩罚值M0=50。

实验1 选取CVRP算例集Set-B、Set-E、Set-P中16个算例，表1给出了张晓楠等[21]提出得HSSA和本文DPHGA的计算结果，*表示最优值。每个算例重复计算20次，其中BKR表示算例给出的当前最优值，Best、Worst、Average分别表示算法计算所得最好值、最差值和均值，Dev表示计算结果同最优值的偏差（Dev=（BKR-Best）/BKR×100%）。

由表1对比结果可知：HSSA可求解出所给算例集中的4个最优值，与最优值的平均偏差为-1.18%;本文DPHGA能够求出8最优解，与最优解平均偏差为-0.50%。在求解精度方面，本文DPHGA求解结果与最优值得偏差明显小于对比HSSA所计算结果，并且DPHGA能够求解到最优解的比例更高，求解稳定，优于所对比的算法。

实验2 选取CVRP算例集Set-A中24个算例，表2给出了对比Sener[22]和Ng[23]提出的LNS-ACO和EBMC-ABC同本文DPHGA的计算结果。每个算例重复计算20次，表2中的符号含义同表1。

由表2对比结果可知：LNS-ACO求解出所给出算例集中的17个最优值，与最优值的平均偏差为-0.44%;EBMC-ABC求解出所给出算例集中的17个最优值，与最优值的平均偏差为-0.17%;本文DPHGA能够求出16个最优值，与最优解平均偏差为-0.19%。在求解精度方面，本文DPHGA求解结果与最优值的偏差明显小于对比LNS-ACO所计算结果，并且与EBMC-ABC计算结果基本一致，本文算法能够求解到最优解的比例更高，求解稳定，优于所对比算法。

如图2所示，标准遗传算法（GA）、模拟退火算法（SA）和DPHGA计算算例A-n37-k5、P-n45-k5、B-n39-k5的收敛曲线对比。可知SA单独计算CVRP算例时，在求解到算例的次优解之后会陷入局部最优，收敛效果较差;相比于SA，GA收敛速度较快，经过大量迭代计算后可以逐步提升解的质量，但在20次重复计算中，很难求解到最优值;相对于SA、GA单独计算而言， DPHGA收敛曲线平缓，无早熟及陷入局部最优情况出现，三个案例均在DPHGA迭代700次左右就逼近算例已知全局最优解。可见，改进双种群混合遗

传算法在求解精度、算法收敛性等方面均得到很大提高，寻优质量较高。

综上所述， DPHGA在求解精度、算法稳定性等方面均优于所对比的5中算法，是求解CVRP问题的有效方法。

五、 结论

本文提出基于改进双种群混合遗传算法求解CVRP问题。算法采用两个种群协同进化的思想，种群II结合遗传算法全局搜索性能及移民策略思想进行算法的全局搜索及开发，扩大解方案的搜索空间，维持种群的高多样性;种群I在传统遗传算法迭代基础上，引入模拟退火思想及变邻域搜索策略，增强算法的局部探索能力。劣势种群进行全局搜索开发，精英种群进行局部探索，然后两种群通过协同进化的机制极大提高了算法搜索到全局最优解的概率。算例验证及分析表明，DPHGA可有效求解CVRP，寻优质量优于对比算法，今后可进一步改进该算法，增强算法求解大规模客户算例的性能。

参考文献：

[1]  VIDAL T， CRAINIC T G，GENDREAU M，et al. Implicit depot assignments and rotations in vehicle routing heuristics[J].  European journal of operational research， 2014， 237（1）： 15-28.

[2] PRADHANANGA R，TANIGUCHI E，YAMADA T，et al. Environmental analysis of pareto optimal routes in hazardous material transportation [J]. Procedia - social and behavioral sciences， 2014， 125（1）： 506-517.

[3] NARASIMHA K V，KIVELEVITCH E，SHARMA B，et al. An ant colony optimization technique for solving min-max multi-depot vehicle routing problem[J]. Swarm & evolutionary computation， 2013， 13（C）： 63-73.

[4] 石兆. 物流配送選址—运输路径优化问题研究[D]. 长沙：中南大学， 2014：30-33.

[5] 刘万峰，李霞. 车辆路径问题的快速多邻域迭代局部搜索算法[J]. 深圳大学学报（理工版）， 2015， 32（2）： 196-204.

[6] 王文蕊，吴耀华. 带实际约束的大规模车辆路径问题建模及求解[J]. 控制与决策， 2013， 28（12）： 1799-1804.

[7] 姜婷. 混合差分蜂群算法求解带容量约束车辆路径问题[J]. 宜宾学院学报， 2017， 17（12）： 52-56.

[8] 毕志升，蔡茗芊. 基于多目标模拟退火的带容量限制车辆路径问题[J]. 计算机与数字工程， 2017， 45（8）： 1513-1518.

[9] 陈亮，周晶晶. 求解CVRP的改进蚁群系统算法[J]. 军事交通学院学报， 2014， 16（5）： 92-95.

[10] 蒋海青，赵燕伟，冷龙龙. 基于化学反应优化算法的车辆路径问题[J]. 计算机集成制造系统， 2018， 24（8）： 2012-2022.

[11] 颜腾威，王丽侠，周杰，等. 求解CVRP问题的改进和声算法[J]. 计算机技术与发展， 2016， 26（9）： 187-191.

[12] 周和平，陈亮. 求解CVRP问题的一种改进启发式蚁群算法[J]. 后勤工程学院学报， 2015， 31（4）： 80-84，89.

[13] 李阳，范厚明. 求解带容量约束车辆路径问题的混合变邻域生物共栖搜索算法[J]. 控制与决策， 2018， 33（7）： 1190-1198.

[14] 夏茂庚，郑阳光，兰延涛，等. 有容量约束车辆路径问题的蒙特卡洛模拟算法[J]. 科学技术与工程， 2012， 12（26）： 6849-6852.

[15] 程子安，童鹰，申丽娟，等. 双种群混合遗传算法求解柔性作业车间调度问题[J]. 计算机工程与设计， 2016， 37（6）： 1636-1642.

[16] 沈斌，周莹君，王家海. 基于自适应遗传算法的Job Shop调度问题研究[J]. 计算机应用， 2009， 29（S2）： 161-164，188.

[17] 易军，李太福. 求解作业车间调度的变邻域细菌觅食优化算法[J]. 机械工程学报， 2012， 48（12）： 178-183.

[18] 张义长，杨加明，鲁宇明. 结合保优策略和移民策略的自适应遗传算法[J]. 计算机工程与应用， 2010， 46（31）： 36-38.

[19] 史峰. MATLAB 智能算法—30个案例分析[M]. 北京：北京航天航空大学出版社，2011：69-79.

[20] CROES G A. A method for solving traveling-salesman problems[J]. Operations research， 1958， 6（6）： 791-812.

[21] 張晓楠，范厚明. 混合分散搜索算法求解带容量约束车辆路径问题[J]. 控制与决策， 2015， 30（11）： 1937-1944.

[22] AKPINAR S. Hybrid large neighbourhood search algorithm for capacitated vehicle routing problem[J]. Expert systems with applications， 2016， 61：28-38.

[23]NG K K H，LEE C K M，ZHANG S Z. A multiple colonies artificial bee colony algorithm for a capacitated vehicle routing problem and re-routing strategies under time-dependent traffic congestion[J]. Computers & industrial engineering， 2017， 109： 151-168.