快速独立分量分析算法解析及其仿真

郁芸 张昕 胡杰 万程 周高信 王捷 殷悦楚楚 冯伟 王娟

[摘 要]独立分量分析（Independent Component Analysis，ICA）是在信号处理领域中关于盲源分离应用的常用方法。该文论述了独立分量分析的基本原理和分离步骤;介绍了快速独立分量分析（FastICA）的优化判据和优化算法特点;并进行了FastICA计算机程序仿真：首先混合了方波信号、正弦信号和噪声信号，再利用FastICA算法进行分离。分离结果，除了波形的波幅、次序和极性发生变化之外，源信号的波形被很好地分离还原出来，证实了FastICA的可行性和正确性。

[关键词]快速独立分量分析;算法;仿真

[基金项目]2018年度江苏省高校哲学社会科学研究项目“基于核磁共振的艾滋孤儿负性情绪研究”（2018SJA0282）

[作者简介]郁 芸（1979—），女，江苏南通人，硕士，南京医科大学生物医学工程与信息学院医学信息学系副主任，副教授，主要从事医学图像处理研究;王 娟（1981—），女，江苏盐城人，硕士，南京医科大学生物医学工程与信息学院智能计算与数学学系讲师（通信作者），主要从事医学大数据研究。

[中图分类号] TP301.6[文献标识码] A[文章编号] 1674-9324（2020）28-0381-02[收稿日期] 2019-11-29

一、独立分量分析和盲源分离

盲源分离是随着数字通信等行业的飞速发展而在信号处理领域兴起的一个新的研究方向[1]。它的主要任务就是在系统传输特性未知和输入信号未知或仅有很少的先验知识的条件下，从系统输出信号来估计系统传输特性以及系统输入信号。

独立分量分析在一个宽松的假设条件下，即假设系统输入信号矢量的各分量相互统计独立，同时允许一定的模糊性存在，即信号幅值和信号分量顺序有不确定性，就可以实现盲源分离，这使得ICA成为盲源分离的主流方法[2]（P263）。

二、ICA数学模型

ICA基本研究思路是以非高斯信号为研究对象，假设有n个未知的非高斯源信号彼此统计独立，此n个输入信号，通过一种未知的方式混合，成为m个混合输出信号。独立分量分析提供了不利用其他的先验信息就能从这m个混合的信号中把这n个未知的源信号恢复出来的方法。

设一组独立的源信号s（t）=[s1（t），…sm（t）]T，经过线性系统A混合在一起，得到一组观测信号x（t）=[x1（t），…xn（t）]T，使用矩阵符号表示为：

三、FastICA

ICA方法分离数据的步骤可归纳为：建立以分离矩阵W为变量的目标函数，目标函数反映了分离变量各分量之间的独立性，通过求目标函数的极值（优化算法），就可以实现分量间的分离。其中主要为以下两个方面：优化判据（目标函数）和优化算法。

优化判据是判断一组信号是否接近互相独立的准则，通常以统计理论、信息理论等方法建立一个目标函数J（W），若某个能使J（W）达到极大（或极小）值，该即为所需的解。

各种目标函数之间的差别主要在于它们的具体形式不同。相同的目标函数，可以采取不同的优化算法，相同的优化算法也可应用于不同的目标函数。FastICA采用了定点迭代的优化算法，具有很快的收敛速度，又称Fixed-point算法。常用的FastICA算法有由A.Hyv?rinen及E.Oja提出的基于峭度的FastICA[4]和基于负熵的FastICA[5]。FastICA算法结合投影寻踪、固定点迭代和牛顿法等快速收敛算法，不需要确定学习步长[6]，适用于各种非高斯信号，可以选择不同的非线性函数从而获得不同的性能。

四、实验仿真

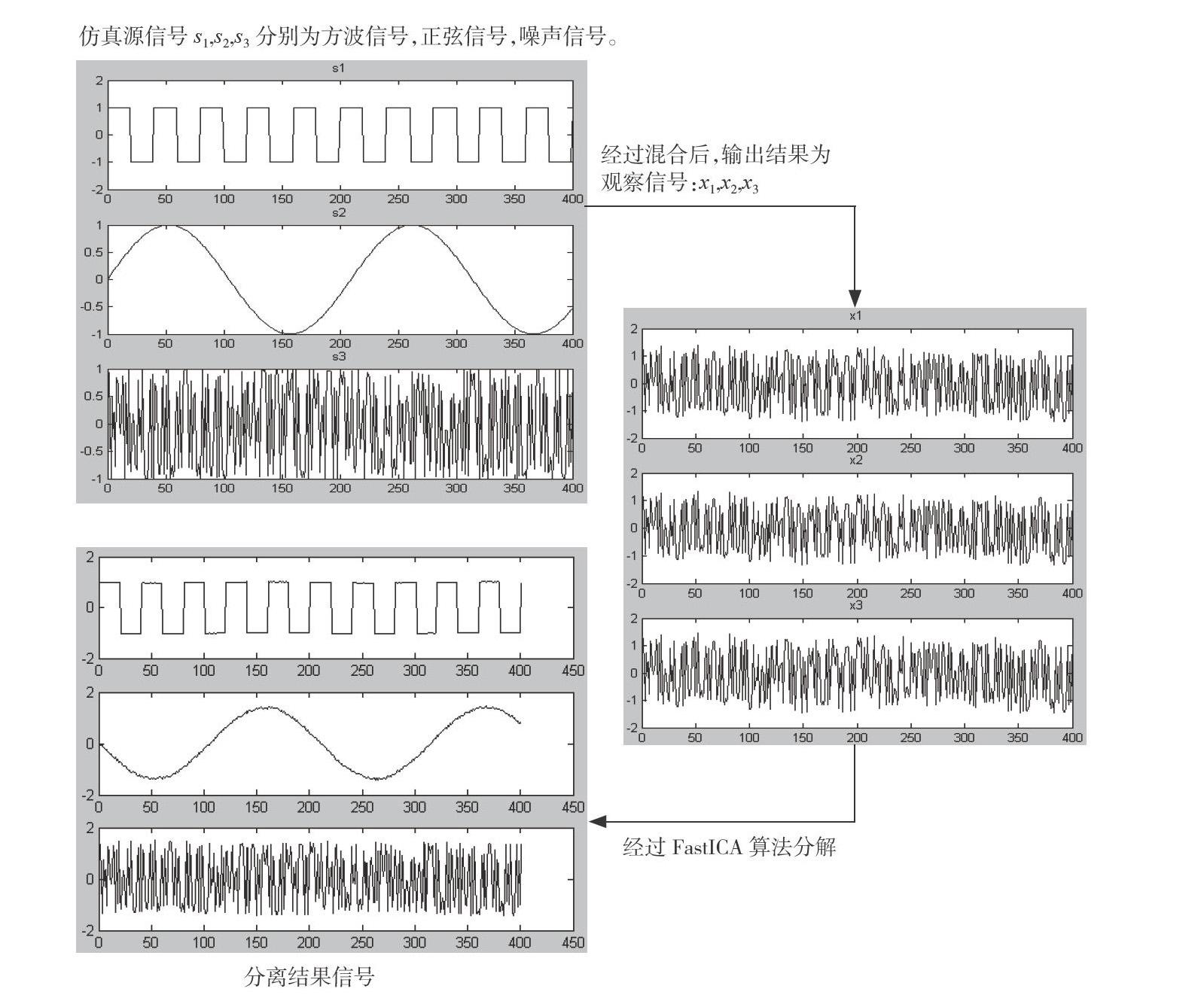
为检验FastICA算法对同时存在超高斯和亚高斯信号的线性叠加信号的分离能力，做了如下图的仿真实验。可以看出，除了波形的波幅、次序和极性发生变化之外，源信号的波形被很好地分离还原出来，同时也反映了ICA问题的不确定性。

五、小结

目前，ICA已经在很多方面获得了实际的应用。在生物医学方面，ICA可用于胎儿心电信号的分离、脑电信号的特征提取等[7]。在图像处理方面，ICA已用于图像特征提取、人脸识别、图像的消噪等方面。在无线通信方面，ICA也已在盲辨识、盲均衡等方面获得了初步的应用。在语音分离问题上，ICA目前是最好的一种技术。在金融数据分析、数据挖掘、生物信息学、机械工程学等其他许多领域中，ICA均获得了成功的应用。

参考文献

[1]Comon P.Independent component analysis，A new concept？[J]. Elsevier，1994，36（3）：287-314.

[2]张贤达.现代信号处理[M].第2版.北京：清华大学出版社， 2002：263.

[3]张旭秀，邱天爽，张润烜，等.獨立分量分析原理及其应用[J].大连铁道学院学报，2003，24（2）：64-69.

[4]Hyv?rinen，A，Oja，E.A Fast Fixed-Point Algorithm for Independent Component Analysis[J].Neural Computation，1997，9（7）：1483-1492.

[5]Hyv?rinen A.Fast and Robust Fixed-point Algorithms for Independent Component Analysis[J].IEEE Transactions on Neural Networks，1999，10（3）：626-634.

[6]杨福生，洪波，唐庆玉.独立分量分析及其在生物医学工程中的应用[J].国外医学.生物医学工程分册，2000，（03）：129-134+186.

[7]鄺亚云，王黎明，王佳琪.基于快速独立分量分析的脑电信号去噪方法研究[J].国外电子测量技术，2018，37（11）：1-4.

Analysis and Simulation of Fast Independent Component Analysis Algorithm

YU Yun， ZHANG Xin， HU Jie， WAN Cheng， ZHOU Gao-xin， WANG Jie，

YIN Yue-chuchu， FENG Wei， WANG Juan

（School of Biomedical Engineering and Informatics， Nanjing Medical University， Nanjing， Jiangsu 211166， China）

Abstract： Independent Component Analysis （ICA） is a wide-used method for blind source separation in the signal processing research field. The basic principles and separation steps of independent component analysis were discussed in the paper. The optimization criteria and optimization algorithm characteristics of Fast Independent Component Analysis （FastICA） were introduced. And the FastICA computer program simulation was carried out. Firstly， the square wave signal， sinusoidal signal and the noise signal were mixed. Then， FastICA algorithm was used to separate them. The separation result shows that except for changes in amplitude， sequence and polarity of the waveform， the source signal waveform is well separated， which confirms the feasibility and correctness of FastICA.

Key words： Fast Independent Component Analysis; algorithm; simulation