高考数学新变化速递
2020-08-13北京付永艾
◇ 北京 付永艾
2020年是实行新高考的第一年,无论是全国卷,还是自主命题省份的高考卷都将有巨大的变化.高考会更注重知识的应用性,强调知识的融会贯通,注重考查创新思维与创新意识.因此,本文主要从新题型和新考法两个方面阐述高考的新变化.
1 新题型
1.1 多选题
相较于单选题而言,多选题对能力的考查更加深入,解题思路广,涉及知识点较多,要求考生进行认真细致的思考与分析.
例1锐角△ABC的三个内角A,B,C所对应的三边为a,b,c,则下列不等式恒成立的是( ).
A.|a2-c2|<b2<a2+c2
B.sinA+sinB+sinC>cosA+cosB+cosC
C.tanAtanBtanC>1
D.tanAtanB+tanBtanC+tanCtanA>3
解析
根据余弦定理不难推出以一个锐角三角形三边平方为长度的三条线段也可以构造三角形,故选项A 正确.
根据三角形内角和定理及锐角三角形的性质不难得出,一个锐角三角形的任意两个内角之和均为钝角,即,进而得出,再根据正弦函数的单调性及诱导公式得,sinA>cosB>0,同理可得sinB>cosC>0,sinC>cosA>0;根据不等式性质不难得出sinA+sinB+sinC>cosA+cosB+cosC及tanAtanBtanC>1,故选项B和C正确.
点评
要想能比较顺利地求解此题,就要对选项逐个进行分析,要求考生对知识内涵进行挖掘,养成运用所学知识分析问题、解决问题的习惯.
1.2 材料自选题
材料自选题是指题目给出多个条件,考生选择其中一种或多种将其纳入题目已知条件之中进行解题.此类试题难度增大,思维量加大.
例2在这两个条件中任选一个,补充在下面问题中,然后解答补充完整的题.
在△ABC中,角A,B,C的对边分别为a,b,c,已知________,.
(1)求sinA;
(2)如图1所示,M为边AC上一点,MC=MB,求△ABC的面积.(注:如果选择两个条件分别解答,按第一个解答计分)
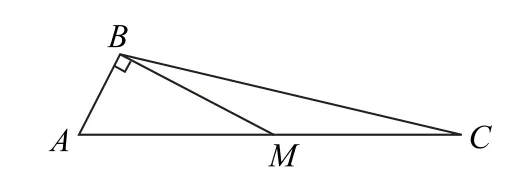
解析
若选择条件①,则答案如下.
(1)在△ABC中,由正弦定理得
3sinAsinC=4sinCcosA.
因为sinC≠0,所以
3sinA=4cosA,9sin2A=16cos2A,
所以25sin2A=16.又因为sinA>0,所以.
(2)设MB=MC=m,易知
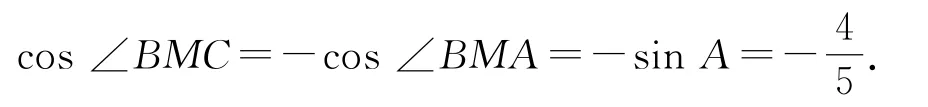
在△ABC中,由余弦定理得18=2m2-2m2·,解得m=5,所以
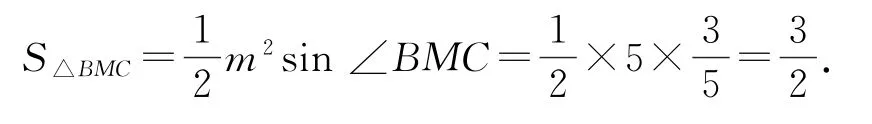
在 Rt △ABM中,,所以,所以所以.
若选择条件②,则答案如下.

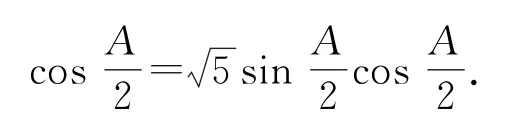
(2)同选择条件①的解析.
点评
求解此类问题时一定要看清题目“如果选择两个条件分别解答,按第一个解答计分”,以免误答、多答,浪费时间.
2 新考法
2.1 素材创新
高考数学将不再单纯考查数学知识,会逐渐创新考查素材,将考点和其他学科知识相结合,渗透德育、智育、体育、美育与劳育等知识.
例3(2019年全国Ⅱ卷)2019年1月3日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆,我国航天事业取得又一重大成就.实现月球背面软着陆需要解决的一个关键技术问题是地面与探测器的通讯联系.为解决这个问题,发射了嫦娥四号中继星“鹊桥”,鹊桥沿着围绕地月拉格朗日点L2的轨道运行.点L2是平衡点,位于地月连线的延长线上.设地球质量为M1,月球质量为M2,地月距离为R,点L2到月球的距离为r,根据牛顿运动定律和万有引力定律,r满足由于α的值很小,因此在近似计算中3α3,则r的近似值为( ).
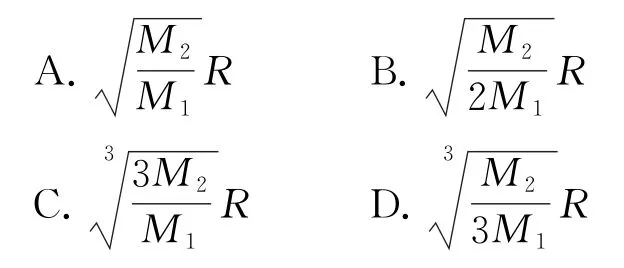
解析
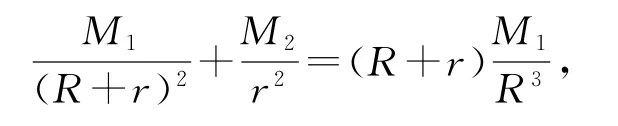
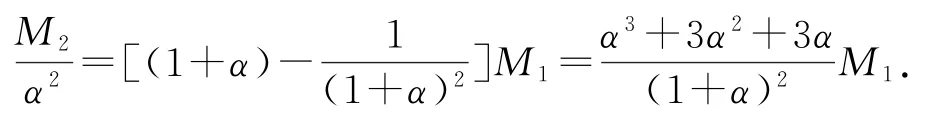
点评
此题以嫦娥四号探测器“鹊桥”有关的背景命题,结合了物理知识与天文知识,体现出不同学科之间的联系,反映了我国航天事业取得的成就.
2.2 选考题调整
从2019年开始,全国卷Ⅰ和全国卷Ⅲ就打破常规,在不等式选考题中不再考查绝对值不等式的求解,相信这样的调整会延续下去.
例4(2019年全国卷Ⅰ)已知a,b,c为正数,且满足abc=1,证明:
(2)(a+b)3+(b+c)3+(c+a)3≥24.
证明(1)因为a2+b2≥2ab,b2+c2≥2bc,a2+c2≥2ac,所以由不等式的性质得
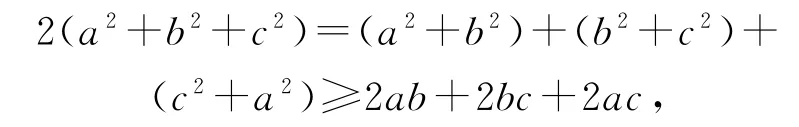
即a2+b2+c2≥ab+bc+ac,当且仅当a=b=c时取等号.
因为abc=1,所以.
(2)由三元均值不等式,可得
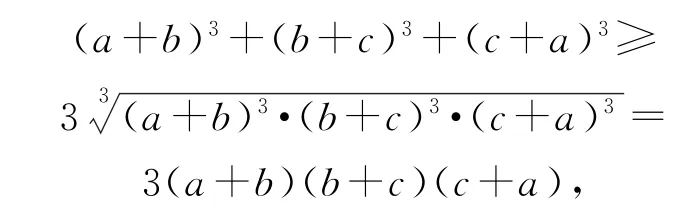
当且仅当a=b=c时取等号.
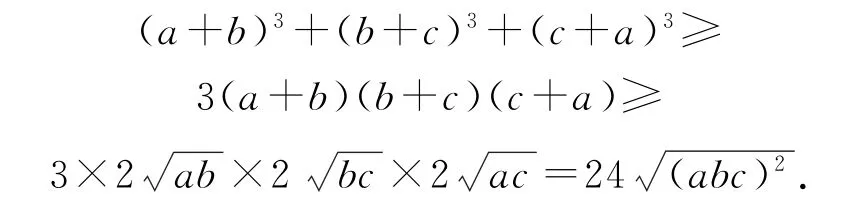
又abc=1,所以
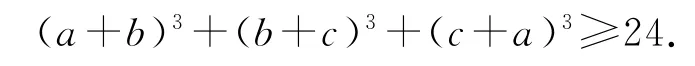
点评
本题考查了运用均值不等式或综合法求证不等式,充分体现了数学抽象、逻辑推理和数学运算等核心素养的要求.
2.3 压轴题变化
压轴题一般是指解答题的最后一道题,压轴题通常较为复杂、难度较大,以导数题居多.2019年全国卷Ⅰ首次出现以概率统计和数列交会的试题压轴,体现出知识融合的重要性.
例5(2019年全国卷Ⅰ)为治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效.为了方便描述问题,约定:对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得-1分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得-1分;若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X.
(1)求X的分布列;
(2)若甲药、乙药在试验开始时都赋予4 分,pi(i=0,1,…,8)表示“甲药的累计得分为i时,最终认为甲药比乙药更有效”的概率,则p0=0,p8=1,pi=api-1+bpi+cpi+1(i=1,2,…,7),其中
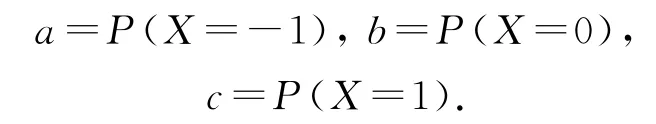
假设α=0.5,β=0.8.
(ⅰ)证明:{pi+1-pi}(i=0,1,2,…,7)为等比数列;
(ⅱ)求p4,并根据p4 的值解释这种试验方案的合理性.
解析
(1)一轮试验中甲药的得分有3 种情况:1,-1,0.
得1分是施以甲药的白鼠治愈且施以乙药的白鼠未治愈,则P(X=1)=α(1-β);
得-1分是施以乙药的白鼠治愈且施以甲药的白鼠未治愈,则P(X=-1)=(1-α)β;
得0分是都治愈或都未治愈,则P(X=0)=αβ+(1-α)(1-β).
X的分布列如表1.
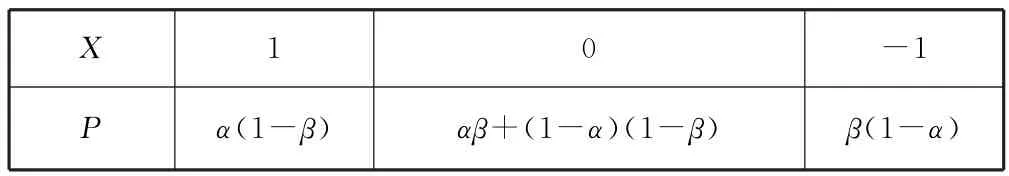
表1
(2)(ⅰ)因为α=0.5,β=0.8,则
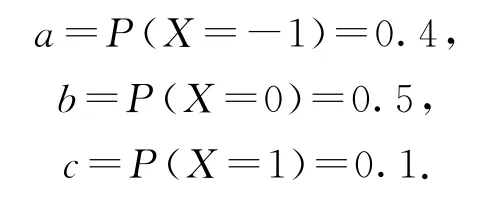
因此pi=0.4pi-1+0.5pi+0.1pi+1,则0.5pi=0.4pi-1+0.1pi+1,即pi+1=5pi-4pi-1.所以.
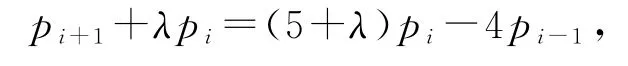

所以 {pi+1-pi}(i=0,1,2,…,7)为等比数列.
(ⅱ){pi+1-pi}(i=0,1,2,…,7)的首项为p1-p0=p1,则可得
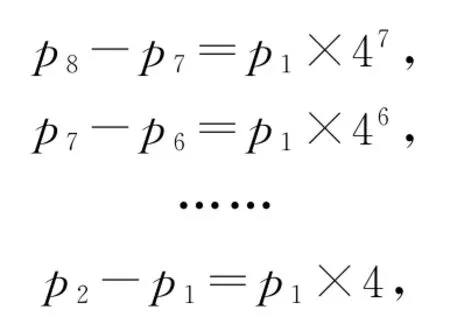
以上7个式子相加,可得
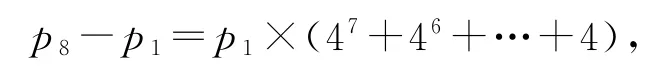
则
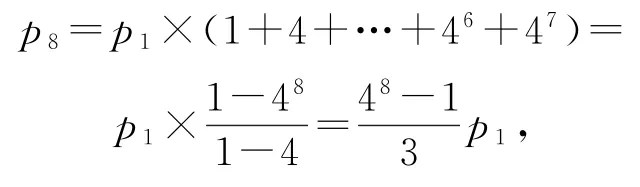
p8=1,则.
再把后面3个式子相加,得
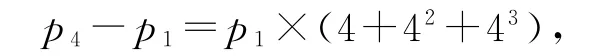
则
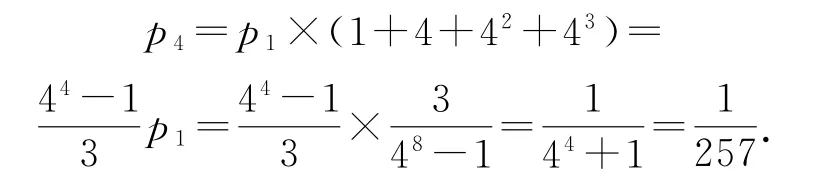
p4表示“甲药治愈的白鼠比乙药治愈的白鼠多4只,且甲药的累计得分为4”,因为α=0.5,β=0.8,α<β,则试验结果中“甲药治愈的白鼠比乙药治愈的白鼠多4只,且甲药的累计得分为4”这种情况的概率是非常小的,而的确非常小,说明这种试验方案是合理的.
点评
此题以试验新药疗效为背景,综合考查了分布列与数列的知识,要求考生具有问题分析的能力,同时需要掌握递推公式的应用.
