量子粒子群算法的柔性交流输电装置协调控制
2020-08-13王利平
徐 飞,王利平
(西京学院 信息工程学院,西安 710123)
0 引言
国内外电力电子技术的快速发展,促进了柔性交流输电技术的应用范围,增强了电网的工作效率,在可操作性、运行速度上也有很大的改善。而柔性交流输电装置(flexible AC transmission system,FACTS)逐渐成为相关领域关注的热点,大量的研究结果表明FACTS装置间出现相互作用的机率较大,更会影响FACTS的控制效果和系统的安全性,电力系统中FACTS装置协调控制是当前相关技术人员关注的热点问题。
目前针对电网的协调控制研究成果较多。文献[1]提出多FACTS元件控制变量配方法与协调投运策略,由于功率冗余大,不能进行系统的无功优化处理,导致协调能力较低。文献[2]提出送端交流电网开机容量分档控制策略,不仅保证电网安全,还提高交直流协调外送能力,但只可对同等类型控制器进行协调控制,具有一定局限性。文献[3]提出综合FACTS和HVDC协调优化的大规模风电脱网控制方法,由于该策略仅针对有功功率波动,不能全面分析控制器中阻尼比等其他稳定性控制指标,因此,协调控制结果不够理想[4]。
本文提出基于量子粒子群算法的FACTS装置协调控制方法,首先构建含动态输出反馈控制的电力系统模型,引入基于阻尼比的系统稳定条件,用于控制电力系统的平稳运行。由于FACTS装置中无功功率会降低发供电效率,因此本文使用量子粒子群算法解决FACTS装置无功优化问题,并通过FACTS装置协调控制指标有效分析控制器间的相互作用进行协调控制[5]。
1 基于量子粒子群算法的FACTS装置协调控制方法
电力系统状态为非线性,本文第一步先分析初步形成的动态模型的与动态输出反馈控制原理,在阻尼比条件下,获得稳定系统的要求,为提出基于量子粒子群算法的FACTS装置协调控制方法做基础[6]。
1.1 含动态输出反馈控制的电力系统模型
对处于平衡位置对动态系统进行线性处理,获取的形式为:
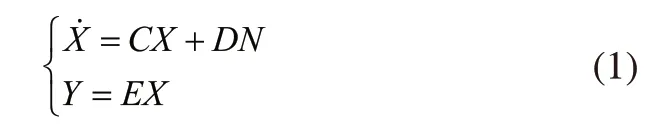
其中,X代表n维状态向量;N与Y分别代表系统的输入控制向量和输出向量;C、D、E描述的是系数矩阵。
控制向量N是根据输出向量Y获取的,如果使用动态线性输出反馈设计,则控制器结构是:
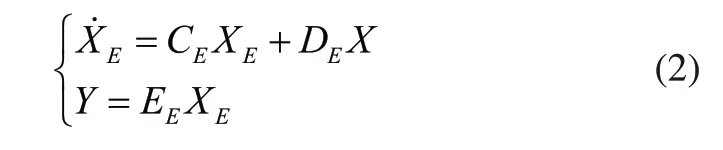
其中,XE描述的是控制器的n维状态向量;CE、DE、EE描述的是系数矩阵。
结合式(1)与式(2)可知电力系统动态状态向量为:

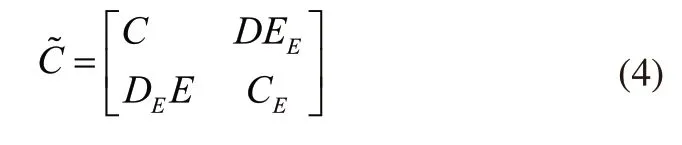
1.2 在阻尼比条件下本文系统的稳定情况
通常判别电力系统稳定性使用Lyapunov方法,对式(3)中的线性时不变系统进行计算,选用Lyapunov能量函数,e代表直径,x代表平衡点。那么系统稳定的必须条件为存在正定的对称矩阵符合线性矩阵不等式(Linear Matrix Inequality,LMI):

但式(5)的成立只可以保证式(3)是逐渐稳定的,系统运行可能会存在弱阻尼模式[7]。根据电力系统的实际需求,系统能够运行于强阻尼模式才可以符合规定。配置系统极点的方法可以在电力系统的阻尼比配置里使用[8]。电力系统里,阻尼比的阈值 ∂0通常设成0.03和0.05,阻尼比不小于这个阈值时系统是处于强阻尼模式中运行。设,便有以下定理。
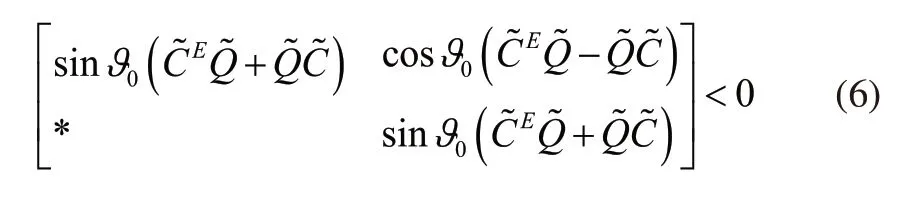
和式(5)对比,这个定理更适合用于研究电力系统的控制问题。
1.3 提高在粒子、粒子群两种算法下的功率策略
感性负荷是电力系统中占比最大的,此时线路中出现感性阻抗,因为线路两端的电压和其中的电流两者之间的相位差是90°,所以功率为0,并且有功功率也为0,而它需要和电源进行能量交换[9],便出现无功功率,会发电机、电网的作用效果会降低。因此对电力系统中的FACTS装置进行协调控制时,需要进行该装置的无功优化[10],即把高压变成低压,以此增强装置的电力传输能力与稳定运行水平。首先对决策变量(装置电压、变压分接头与无功补偿量)实行量子染色体的编码和种群初始化,然后根据解空间变换[11],完成量子染色体和决策变量的对应,最后目标函数通过潮流计算获得,并对其是否可以匹配良好进行分析,储存个体最优信息与全局最优信息,保持最新的量子门,完成种群进化。
1.3.1 初始种群的产生
依据下述三种类型判别初始点的取值范畴,本文采用初始粒子群众实行潮流计算。
1)过多节点电压大于上限,FACTS装置属于无功大量过剩状态,必须引入感性无功补偿设备、减小电压或者去除冗余无功补偿设备。
2)过多节点电压小于下限,装置属于严重缺少无功状态,必须增大电压或引入容性无功补偿设备。
3)较少节点电压小于下限或这大于上限,剩下的每个节点电压稳定,装置处于无功基本平衡状态。
产生初始种群的标准是:分布节点时必须大于目前值的范畴内。
1.3.2 状态变量的处理
FACTS装置电压:以连续量处理,初始运行值按照电压特定的上下边界范畴里随机初始化。优化时,其值更新于边界范畴里;有载变压元件与电容元件:进行离散变量处理,初始运行值产生于规定的上下限里。优化时采用映射编码与取整的形式对离散变量实行处理。针对一个变化调节范畴在[Onmin,Onmax]之间,一共含有n个单位分接头的变压器,调节步长是Ostep={Onmax-Onmin/(n-1),假定第n维控制变量A[n],那么让A[n]的取值范围与分接头的档数相同,则1≤A[n]≤1。根据On=Onmin+[A[n]-1]Ostep把A[n]变换成对应的变比值带入目标函数实行计算,其中[.]代表取整。
1.3.3 FACTS装置无功优化步骤
使用基于量子粒子群算法对FACTS装置实施无功优化的流程是:
1)设置控制变量的维数和其范围,设置量子粒子群算法的种群数量、最大迭代代数、惯性权重、自身因子和全局因子;
2)初始潮流计算,按照无功优化的本质依据倾斜分布方式产生原始粒子种群,同时设置目前进化代数ietr=1;
3)概率幅的初始化;
4)进行解空间变换后计算种群适应度,假设粒子自带的最优位置没有当前所处位置合理,那么使用当前位置代替;如果当前全局最优位置比已经记载的全局最优位置好,那么使用当前全局最优位置代替;
5)更新粒子状态;
6)判别是否到达最大迭代次数,如果是,程序结束。反之回到第4)步。
1.4 FACTS装置协调控制指标
如果电力系统里N台FACTS控制器都可以稳定的进行操作,系统的操纵变量向量和输出变量向量分别用a、y来描述;j代表行数,j∈{1,2,…,n};ai、yi分别为第i行操控变量和输出变量;代表去除第j列元素的输出向量;针对任意操纵变量aj和yj组成的回路,从aj至yj的开环传递函数是zij;代表去除控制器因子zij后的第i行向量和第j列向量。
设定随意两台阻尼控制器zCi和zCj,在zCi开环,zCj闭环状态下,有:

定义下述指标对FACTS阻尼控制器相互作用风险,并进行对比总结,使控制器zCi可以和控制器zCj协调稳定运行。
指标一:设定多FACTS阻尼控制器相互作用风险因子是:
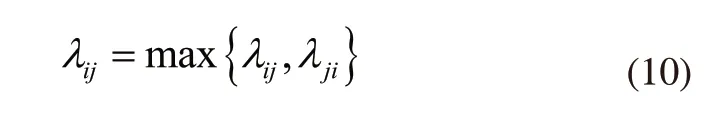
此指标能够对任两个FACTS阻尼控制器间的相互作用的风险高低进行对比分析,它的特征是:
1)λij=1代表控制器间相互作用风险非常大,必须协调控制器;
2)0.8<λij<1代表控制器间相互作用风险很大,需要协调控制器;
3)0.5<λij<0.8代表控制器间相互作用风险较大,提议协调控制器;
4)λij<0.5代表控制器间相互作用风险不大,不用协调控制器。
指标二:多FACTS阻尼控制器交互因子的计算公式是:
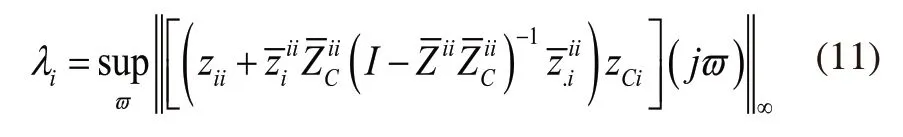
1)λi=1或者邻近1的时候控制器之间的相互作用明显,需要处理;
2)λi=0或者邻近0时控制器之间的相互作用不大,不必处理;
3)λi=0.8代表控制器之间存在相互作用,而系统没有异常,不用处理;
4)λi≥0.8代表控制器之间的相互作用非常大,必须处理。
上述两指标加在一起,便能分析控制系统里随机几个阻尼控制器间的相互作用,有利于对FACTS装置进行全面协调控制。
2 仿真实验
2.1 相同类别 FACTS 协调控制的相互作用分析
送电设备具有距离远、带电量大的特点,所以会产生比较明显的低频振荡问题,本文实验以两机系统为例,验证本文提出的基于量子粒子群算法的FACTS装置协调控制方法的有效性,在两机系统中装置FACTS控制器,分析该两机系统一起运行时存在的交互影响现象。图1是典型的两机系统结构图。
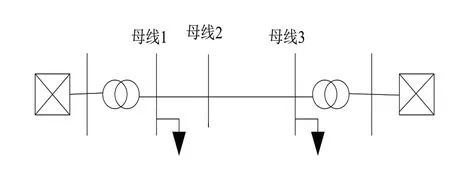
图1 典型两机系统
在图1系统中的两个位置上分别配置SVC,分析本文方法在相同类型FACTS控制器相互作用影响下工作效果。SVC1配置在母线1上,SVC2配置在母线2上。图2和图3中描述的是SVC1和SVC2装置本文方法控制下FACTS控制器后,在有阻尼控制器和无阻尼控制器下的协调控制结果。采用本文方法控制下2台SVC间的相互作用的结果用图4来描述:
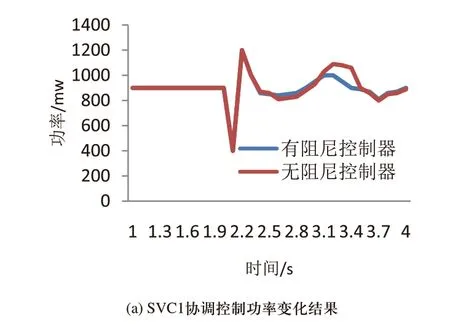
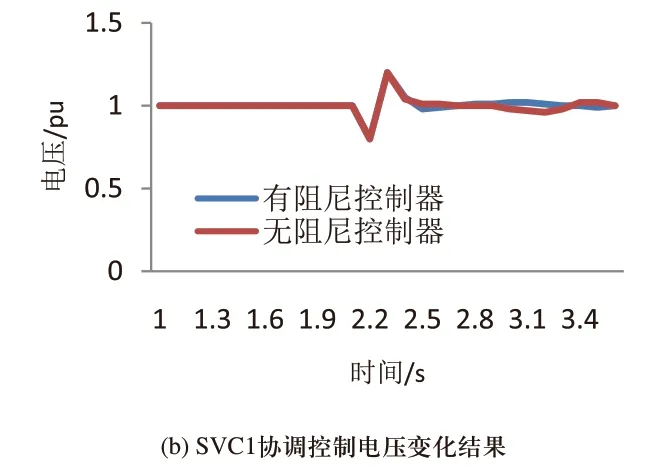
图2 SVC1协调控制结果
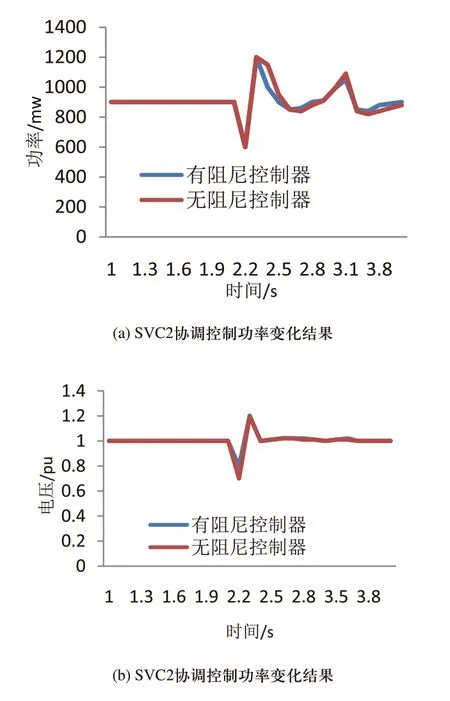
图3 SVC2协调控制结果
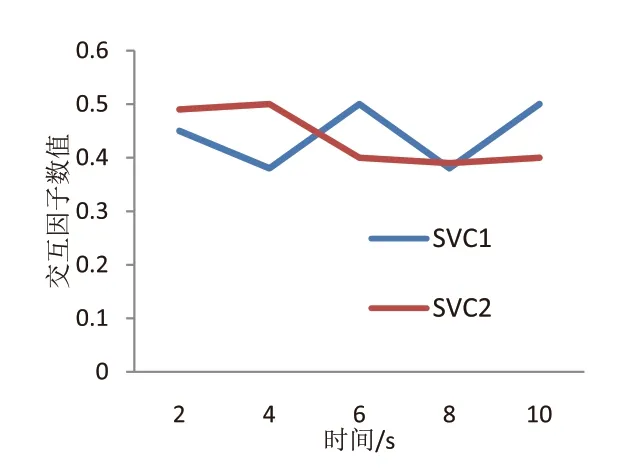
图4 基于本文方法的SVC1和SVC2相互作用
分析图2和图3可知,在装置本文方法控制下FACTS控制器后,SVC1和SVC2在有无阻尼的状况下都可以正常运行,功率和电压走势未出现异常差距波动,说明本文方法控制下得FACTS控制器可确保SVC1和SVC2正常运行,验证了本文方法的有效性。
分析图4可知,在两个组合后的SVC阻尼控制器运行10s后,SVC1的交互因子数值最大值为0.5,最小值为0.38,SVC2的交互因子数值最大值为0.5,最小值为0.39,根据本文方法提出的FACTS装置协调控制指标分析可知,控制器间相互作用风险不高无须再进行协调控制。
在SVC1与SVC2两个阻尼控制器中加入本文方法控制下的FACTS附加阻尼控制器,则构成了控制器1和控制器2,采用本文方法进行控制后两种组合阻尼控制器之间的协调控制结果,结果如表1所示。
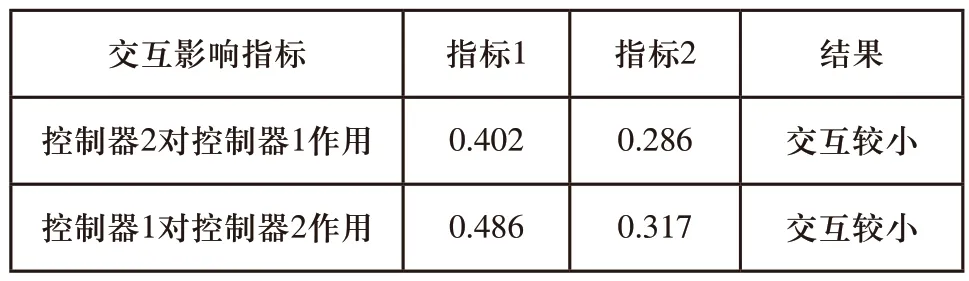
表1 本文方法控制下两种组合阻尼控制器间的相互作用结果
分析表1可知,装置FACTS控制器后的2台SVC的交互影响指标数值都小于0.5,说明控制器1和控制器2间交互效果较小,无需进行协调控制,说明本文方法可实现相同类型FACTS装置的协调控制。
2.2 不同类型FACTS协调控制的交互影响分析
将FACTS装置在不同位置的SVC与STATCOM上,分析基于本文方法的两种不同类型控制器协调控制时相互作用。SVC配置在母线1上,STATCOM配置在母线2上,分析结果如图5与表2所示。
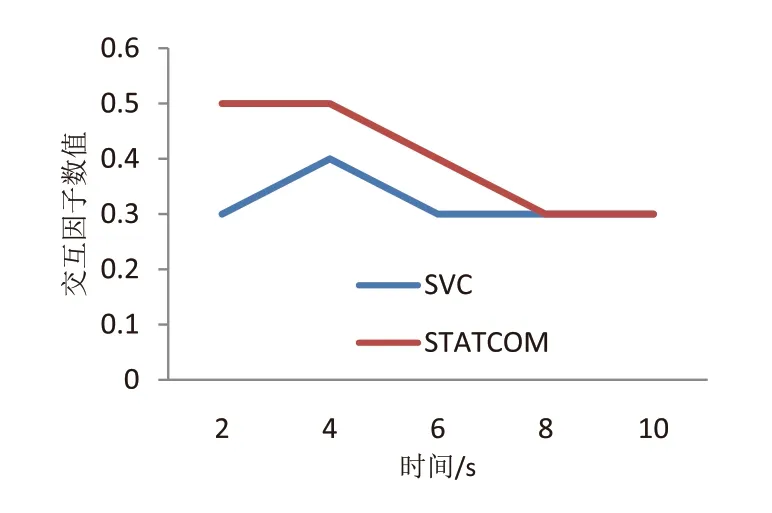
图5 本文方法的SVC 和STATCOM 间相互作用分析
分析图5可知,本文方法下采用FACTS装置后的SVC和STATCOM运行10s后,控制器间的交互因子数值最大值分别是0.5和0.4,都不大于0.5,因此可知基于本文方法的SVC和STATCOM 2台控制器间相互作用较小,两者能够协调运行。
本文方法的SVC和STATCOM间相互作用分析结果如表2所示。分析表2可知,本文方法下采用装置FACTS控制器后的SVC和STATCOM的交互影响指标数值都小于0.5,说明控制器间相互作用风险不高,不需要进行协调,由此可知本文方法可实现不同类型FACTS装置的协调控制问题。
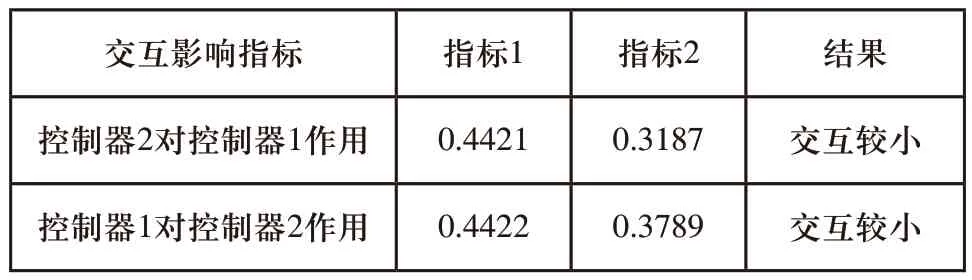
表2 本文方法的SVC和STATCOM间相互作用分析结果
3 结语
提出了基于量子粒子群算法的FACTS装置协调控制方法,分析动态模型的基本形成与动态输出反馈控制原理,导入基于阻尼比的系统稳定条件,可有效控制系统平稳运行;采用基于量子粒子群算法的无功优化策略,使得FACTS装置中的有阻尼控制器和无阻尼控制器平衡运行,变压器把高压变成低压,增强装置的电力传输能力与稳定运行的水平;最后通过FACTS装置协调控制指标分析使用本文方法后电力系统中控制器的相互作用,判断电力系统的安全性。实验结果表明,本文方法对相同类型的控制器和不同类型的控制器协调控制后控制器的交互因子值均不大于0.5,说明本文方法控制效果好,具有较高的使用价值。
