NARX神经网络在电缆绝缘厚度滞后控制系统中的应用与仿真
2020-08-13周克良张宇龙杨国炜
周克良,张宇龙,杨国炜
(1.江西省赣州市江西理工大学 电气工程与自动化学院,赣州 341000;2.江西省赣州市江西理工大学 机电学院,赣州 341000)
0 引言
本文将对电线电缆产品的制造进行研究,确切来说,是对与产品规格书中明确规定的绝缘电缆厚度值进行研究。电线电缆是我国重要产业[1],对于其塑料涂层的控制是一个典型的挤出过程控制问题,其中对塑料绝缘厚度的要求是产品质量的主要指标之一。在过去的几十年中,工业界运用了非常多的方法对挤压模具对聚合物的挤出进行了控制[2~11],但很少有论文对于绝缘电缆厚度的控制及其在控制期间将出现的强滞后问题进行研究。
在日常的控制领域中,对于绝缘电缆厚度控制最经典的方法就是PID控制,该方法普遍运用于大多数生产车间中,但是该方法在对电缆线径及厚度要求更加精密的现代精度要求已经难以匹配。首先,对于PID三个参数的设置就是一个难点,并且鲁棒性较低。其次,对于绝缘电缆这种强滞后系统,只能通过挤出行程以及挤出速度来计算滞后时间,因此而导致响应速度慢,超调量大。以下是一部分学者对于电缆线径或电缆绝缘厚度的控制方法研究:
文献[12]提出了一种结合级联控制和前馈控制的优点,实现附加效益的组合控制策略。组合控制系统将弥补模型中的各控制方法单独控制系统的缺陷;此外,它将减少不可测扰动的影响。该方法可推广到其他生产线,如轧钢机生产线、橡胶生产线等。但是该方法是根据当前测得的线径值对挤出速度进行控制,在滞后系统中控制精度将大大降低。
文献[13]提出了ACO-KF-PID算法,采用蚁群算法寻找PID算法在滞后情况下的最优参数,并进行在线调整,同时引入卡尔曼滤波算法对工作中的噪声和扰动进行抑制。该方法在一定程度上有效抑制了滞后对于控制系统的影响。
文献[14]提出了一种改进Smith预估器对传递函数中的滞后项进行处理,该方法在Smith预估控制方案的基础上,利用模糊PID对线径进行控制。该文献在一定程度上能完全解决滞后性问题,但是会对传递函数产生一定的影响,导致控制系统出现一定的偏差。
由于近些年来机器学习以及人工智能的高速发展,机器学习的应用领域被普及到了各个领域。若是可得出更为精确的离散化模型,可将模型代入人工智能中进行预测与决策。本文拟采用NARX神经网络(Nonlinear Auto-Regressive Neural Network)建立当前电缆线径的离散化数学模型,得出与当前输出值相关的因素与历史输入量以及它们的相关性,并通过相关的性能参数对神经网络的性能进行评估。
1 电缆挤出工艺分析
绝缘挤出生产线作为电线电缆制造行业的生产工艺,设备组主要包括:放线机构、挤出机、线径测试仪、冷却装置、牵引装置、收卷机构等。其工艺流程图如图1所示。
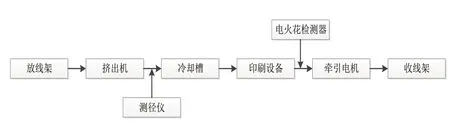
图1 绝缘挤出生产线工艺流程图
在一定的情况下,电缆的线径主要取决于绝缘层的厚度,而绝缘层的厚度主要取决于两个因素:即挤压和牵引速度。绝缘材料的挤出流量由挤出机的工作原理决定,系统的主要牵引速度主要由牵引设备决定。
挤出机的工作原理是利用螺杆旋转机构,包括进料斗运送均匀的绝缘熔融材料到加热桶内,绝缘材料的熔化状态连续传输到机头模具的内部,将绝缘材料挤压成绝缘层所需的形状,挤压在导体上。
本文主要研究的滞后问题,产生的原因在于测径仪一般安装在离机头较远处的位置,而传统的车间一般采用当前测得的线径值反馈给控制器,来控制当前的推挤速度,这样就导致了在若干个时间点之前的线径值对当前的推挤速度进行了控制,从而出现控制偏差。其中,在稳定的牵引速度下,滞后时间的求解公式为:

其中l为测径仪到机头的距离,Vtraction为牵引速度。文献[15]通过机理建模,从而建立了线径控制系统的非线性微分差分数学模型,并分析了该模型的稳定性,本文的研究通过该文献建立的模型的挤出上进行:
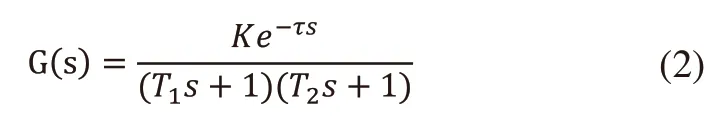
其中K为比例系数,又称放大因子,T1和T2分别为大小惯性时间常数,τ为滞后时间常数。则输入控制量(推挤速度)与输出值(线径)之间的关系为:
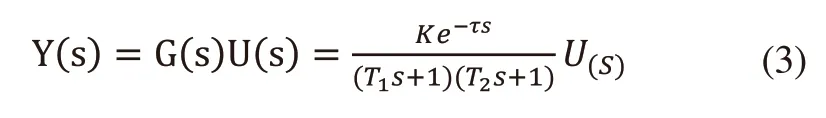
由于式(3)为连续模型,需要将其离散化以便通过迭代以及拟合,确定各滞后项的系数,故将其按照取样周期T来进行离散化:
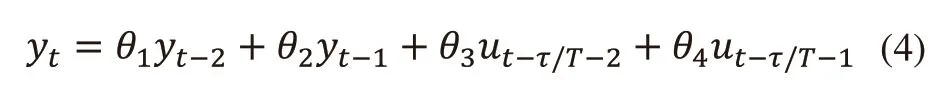
在式(4)中,系统t时刻的输出yt,仅与系统t-2时刻的输出yt-2、系统t-1时刻的输出yt-1、系统t-τ/T-2时刻的输入ut-τ/T-2、系统t-τ/T-1时刻的输入ut-τ/T-1有关,线性系数分别为θ1、θ2、θ3、θ4。但根据第1章所述,在传统离散化模型中,当前电缆绝缘厚度输出值精度不够,故需要对更多的输出值历史量进行代入与拟合。
而在实际生产中,由于一部分外界影响因素是无法控制的,根据文献[12]所提出的模型,电缆绝缘厚度还与以下外部因素决定:
-挤出机工作区的温度和挤出机模具的温度;
-模具几何形状;
-螺杆转速;
-聚合物涂层的物理和流变特性;
-收卷驱动单元的线速。根据以上对于工业中的变量分析,可得出以下数学模型式:
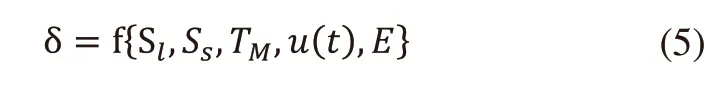
其中,δ为电缆的绝缘厚度,Sl代表收线单元的卷线速度,Ss是螺杆速度、TM表示一个描述挤出机工作区域温度和挤出机模具温度的函数,u(t)代表挤出机模具的挤出速度,E是一个常数,取决于聚合物涂层的物理和流变特性。
由于外部影响因素较多,在该情况下,需要引入对模型要求不高的算法,对其进行训练与验证以及预测,这就考虑到了神经网络算法,得出的拟合结果将与离散化结果(4)进行对比验证。
2 NARX神经网络
2.1 NAR神经网络算法
从神经网络的特点来分析,动态神经网络对于线径控制这类由时间序列模型。典型的时间序列神经网络包括NAR与NARX神经网络。
NAR神经网络中,时间序列y(t)仅与历史值相关,根据历史值来进行预测。其关系如下所示:

式中,t表示为时间,n为时间序列的延迟阶数。
NAR神经网络一般由三层神经网络构成,其分别为输入层、隐含层与输出层,其基本构成如图2所示。

图2 NAR神经网络结构示意图
而本文函数逼近方式为梯度下降法,其数学定义式如下:

令J(θ)最小化,即模型预测线径值理想线径值之间的误差达到最小值。
而本文所得到的差分方程得出线径输出值与其历史值以及滞后时间之前的输入(即挤出速度)值的有关,这就表明需要在NAR的输入基础上附加一个外部变量输入项,而这就需要使用NARX神经网络,即在一维时间序列线径值中插入外部输入挤出速度。
2.2 NARX神经网络算法
对应NAR神经网络,NARX神经网络中,时间序列y(t)不仅与y(t)的历史值有关,同时还引入另外一个时间序列x(t),用以构建y(t)与y(t)历史值以及x(t)历史值得数学模型,该类形式的预测被称为具有外部输入的非线性自回归,其数学表达式为:
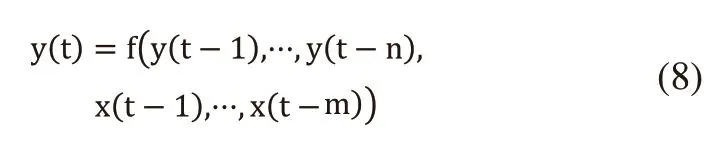
式中,m表示外部输入时间序列x(t)的延迟阶数。
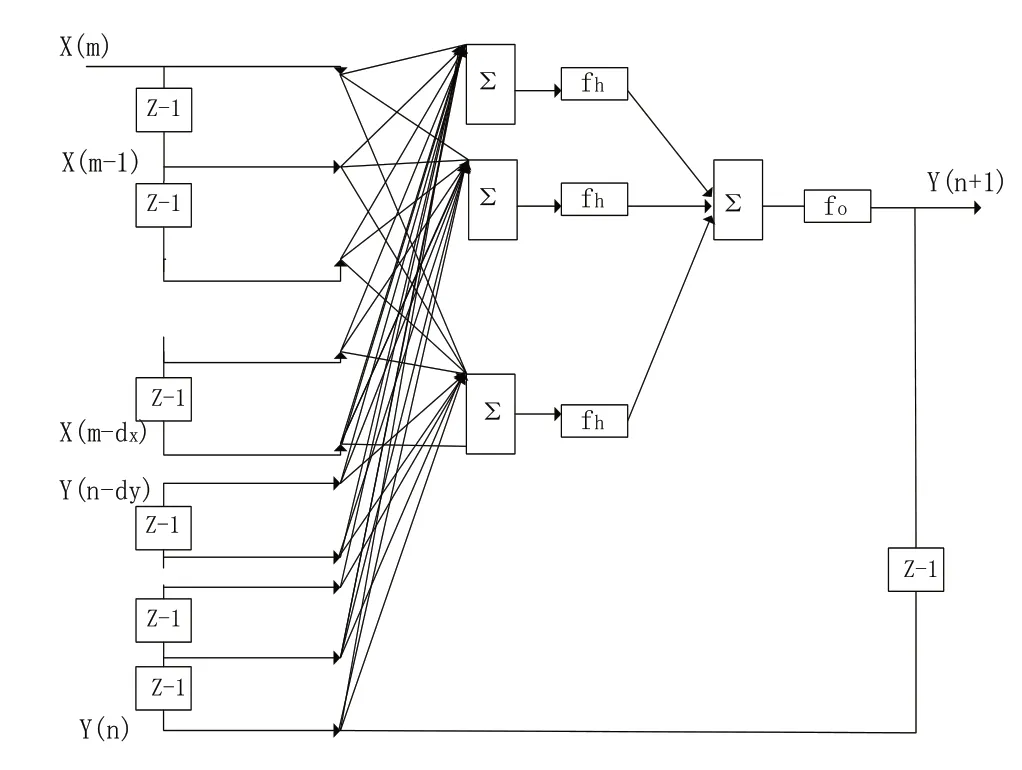
图3 NARX神经网络结构示意图
图3为NARX神经网络的结构示意图,其中Z-1为延迟层。可以直观地得出,NARX在NAR神经网络输入时间序列上附加了一个或多个外部输入变量,再将外部输入变量时间序列通过延迟层进行差分,然后进入神经网络中进行训练,拟合出对于y(n)时间序列的数学模型,同时对y(n+1)时间序列进行预测。
在使用NARX比较外部变量的相关性过程中,常用输入变量选择的方法有灰关联分析法、主成分分析法、遗传算法等方法,其中,灰关联分析法简单且稳定性好。本文采用人工观察筛查结合灰关联分析法进行模型输入变量的初步选取。灰关联分析法通过计算比较序列与参考序列样本数据的灰色关联度值,判断二者之间相对变化趋势,从而确定二者之间的关联程度。常用的灰关联分析关联度有邓氏灰色关联度、相对变化速率关联度、斜率关联度。描述事物发展过程比较合理的指标一般采用相对变化速率,若相对变化速率基本一致,则可认为2个序列有较高的相关程度。因此,本文采用灰关联分析法中的相对变化速率关联度确定输入变量。
2.3 数据预处理及参数调整
本文通过收集赣州某电缆制造公司车间所读取的数据,以及工艺流程中的传递函数完成本次实验。其中,数据包括收卷速度,螺杆速度,挤出速度,挤出模具温度以及电缆绝缘厚度值。而所选取的输出值与挤出速度之间的传递函数为:
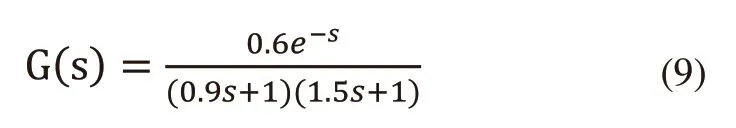
式中,滞后时间τ=1s,选取采样周期为0.1s,故有滞后阶数为τ/T=10。根据式(4)所得模型可得出,-(τ/T+2)=-12。则根据离散化模型可知电缆绝缘厚度仅与y(-11,y(t-12)相关。本文实验中将把现场所测得的实时数据分为各个一维时间序列代入神经网络中进行拟合。
3 实验结果及其效果验证
本文选用软件以及平台为MATLAB中Neural Net Time Series工具箱,该工具箱在研究时间序列输入方面具有较强优势,可灵活选取隐含层数,延迟层数,以及学习率与函数逼近方式,其用户界面友好,这都是本文选择该平台作为线径滞后系统拟合工具的原因。硬件设施都是在PC中完成,处理器为Intel Core I7@3.4GHz,内存8GB。
将数据集引入工具箱中进行神经网络训练与测试,以下为实验过程与仿真结果图。
表1为经过神经网络训练前,经过NAR神经网络以及NARX神经网络训练后的实验结果,该实验选取隐含层数为默认值1层。
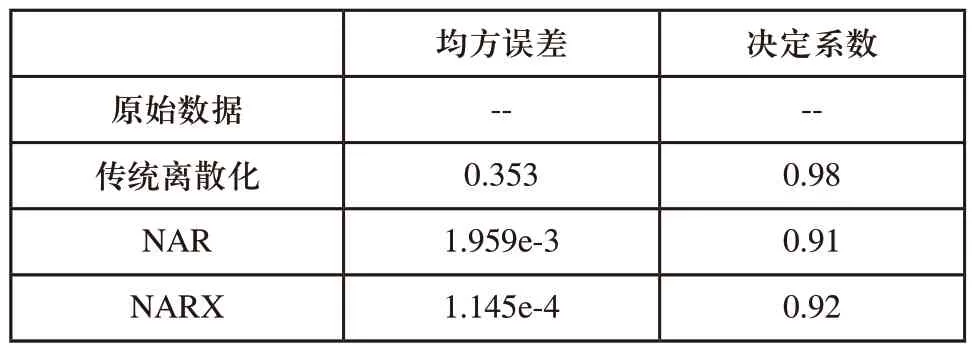
表1 时间序列神经网络性能参数
表1中,均方误差(MSE)为神经网络的默认性能参数,其数学计算公式为:
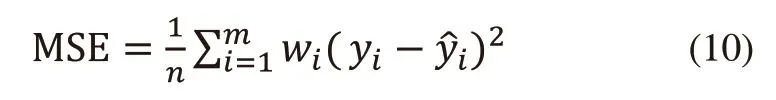
式中,m为样本个数。而决定系数R2代表神经网络输出值与实际值之间的相关系数,其数学计算公式为:

为了确定滞后深度对于控制的影响,本文将利用控制变法对延迟层进行递增,通过每一次拟合的MSE以及R2的变化率以确定离散化传递函数模型。根据第2章工艺分析可知,输入时间序列仅与最近的输入值有关,故延迟层数不需设置过大,以防进入第二个滞后周期进行拟合控制,并且可以减小不必要的计算复杂度。表2为输出延迟层从1到τ/2T的拟合均方误差以及决定系数。
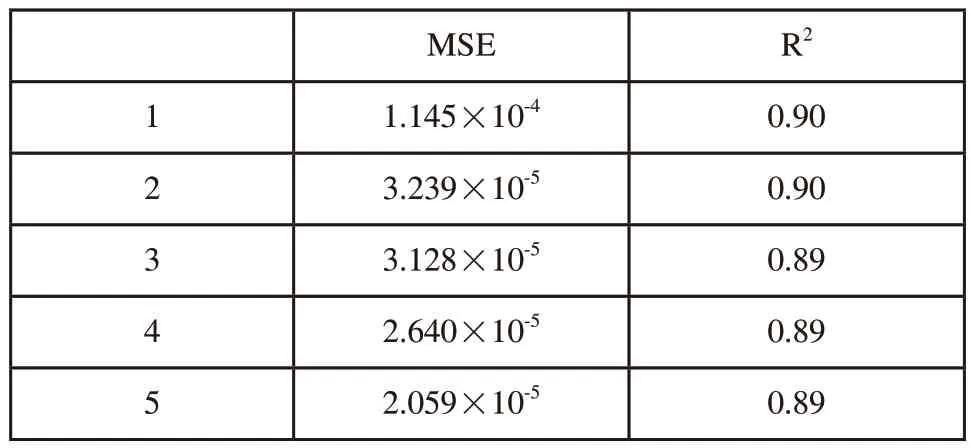
表2 各输出延迟层对应的神经网络性能参数
根据表1与表2可以直观地得出,输出时间序列yt与yt-1以及yt-2的相关性比较大,在延迟层继续向上增加时,误差下降速率大幅度下降,但下降速率还在与加入yt-1与yt-2在一个数量级上,而在训练时间上也在可进行预测控制的范围以内,故若需进行更为精确的控制,yt-3,yt-4,yt-5也可以代入离散化传递函数中进行处理。
在3.3章中已经得出,根据对于工艺流程的分析,输入历史值至少在滞后阶数为τ/T=10之上才能对当前输出值y(t)进行控制。故本文选取延迟层为10~15层。表3为选定延迟层数为τ/T至15层的神经网络性能参数(选定输出延迟层为5的情况下)。
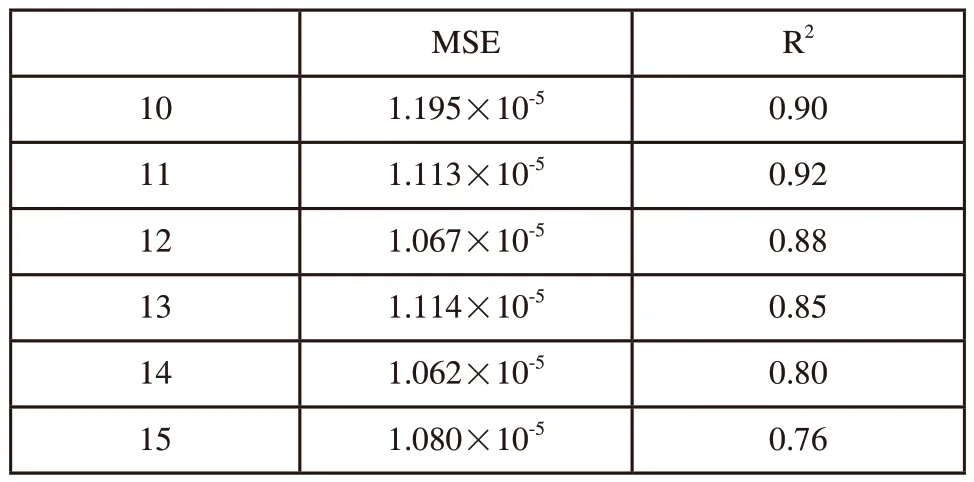
表3 各外部输入延迟层对应的神经网络性能参数
根据表3可得,当外部输入延迟层选取为11层时,性能比较其他为最佳。当延迟层大于11层时,决定系数将大幅度降低,换句话说,拟合曲线与原数据曲线的关联性大幅度降低,神经网络的拟合效果变差。故实验选取外部延迟层数为11层为最佳。
当选取好外部输入延迟层以及输入延迟层后,本文就可以对电缆绝缘厚度以及其外部各项输入量进行训练,拟合,从而达到预测和控制的效果。
根据第二章式(5)所示,确定将挤出机模具的温度、螺杆转速以及收卷驱动单元的线速作为除传递函数中输入值挤出速度外的另外三个输入变量,将挤出速度标记为序号1,其余3个变量根据顺序标记为序号2,3,4。下表为输入多变量时NARX神经网络模型计算误差值以及决定系数。
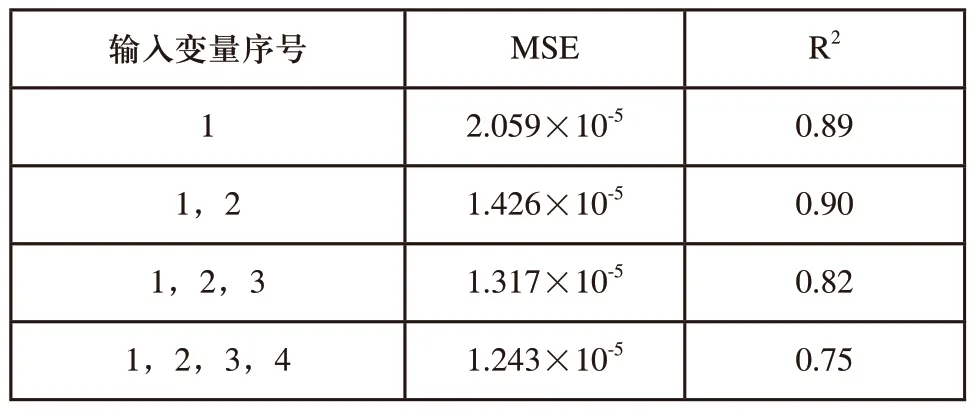
表4 输入多变量时NARX神经网络模型计算误差
根据上表结论,以及灰关联速率分析法结论,电缆绝缘厚度与温度还有较高的关联性,而决定系数R2也证明了该相关性。将上述确定的输入变量的结论取出,分别与初始数据,NAR神经网络拟合数据以及NARX输入变量为挤出速度与挤出模具温度,部分对比结果如图4所示。

图4 各方法的实验结果仿真图
根据图4可直观得出,在选取上述神经网络参数后的NARX回归拟合模型对比原始数据以及NAR的效果出色。
在得到对比传统离散化模型更为精确的数学模型之后,将该离散化模型作为传递函数代入PID控制中(选用输入为阶跃函数,阶跃值为1),得出的控制曲线如图5、图6所示。

图5 τ=0时PID控制曲线
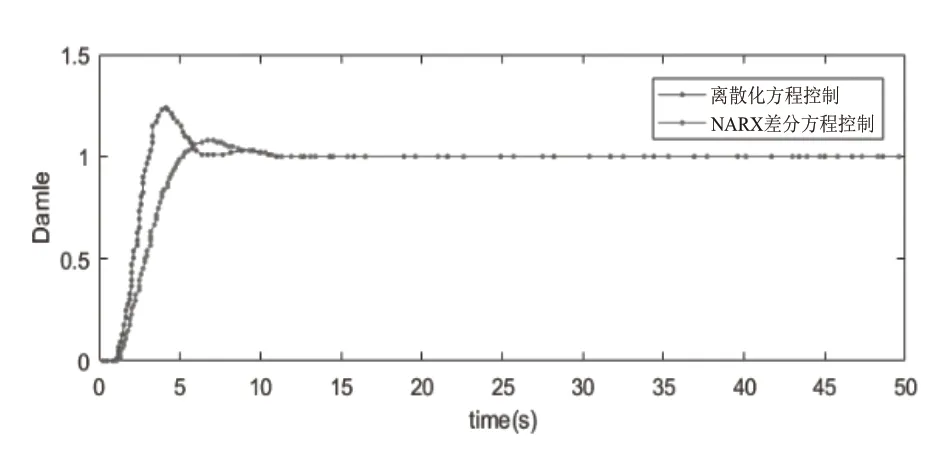
图6 τ=1时PID控制曲线
由图5、图6可以得出,当延迟时间τ=0时,即控制系统为非延迟系统时,采用传统离散化差分方程与NARX神经网络拟合差分方程运用PID控制的效果相差无几。而当延迟时间上升,采用τ=1时,采用NARX神经网络的超调量,稳态时间,振荡幅度等控制性能参数都要全面优于传统离散化方程所得到的差分方程。
4 结语
针对具有滞后特性的电缆绝缘挤出机,本文设计了一种基于NARX神经网络方法,构造出对于现场而言更为精确的差分方程,并代入PID控制器里面进行仿真控制,并在不同滞后时间下,与传递函数离散化形成的差分方程进行了仿真对比实验,结果表明NARX神经网络构造的差分方程进行控制具有响应速度和收敛速度快,超调量小等优点,能够轻松应对像电缆绝缘挤出机一样,内部环境未知并且又有滞后的控制系统,因此该算法该可以推广到类似的具有该特性的控制系统。
