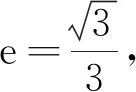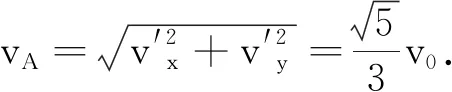紧扣物理规律 着重思维训练 培养物理建模能力——以碰撞模型为例

李 惠

(株洲市第二中学 湖南 株洲 412000)

【例题】水平光滑大桌面上有一质量为M的均匀圆环形细管道，管道内有两个质量同为m的小球A和B位于管道同一直径的两端.t=0时刻管道静止，小球A和B沿着切线方向有相同的初速度v0，如图1所示.不计一切摩擦.

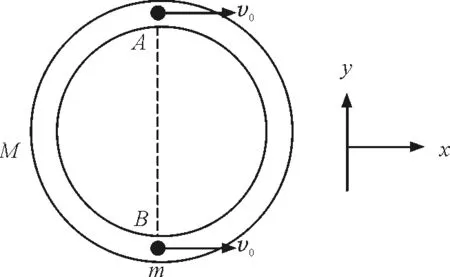
图1 例题题图

(1)两个小球在管道内第一次相碰前瞬间的相对速度大小.

(2)设两个小球的碰撞是弹性的，分析两小球碰后能否在管道内返回初始时刻相对管道的位置？

(3)若能，再通过计算确定两小球到达这个位置时相对于大桌面的速度方向.

这是2008年北京大学自主招生考试的最后一题.笔者选择这道题作为讲解完一维对心碰撞模型后的一道习题对学生做竞赛培训，在培训中，为了让学生能进一步深化物理规律，笔者在此题的基础上，设计了3处改动，着重对学生思维能力的训练，以期能够在较短时间内建立起正确而适合的物理模型来解决新的问题.本文把这一培训过程展现出来.

1 参照一维碰撞模型 紧扣物理规律 引导学生提炼“新”情境中的“旧”规律

我们来回顾一维碰撞模型，为了更直观地“看到”碰撞这一极短时间内的内力作用过程，我们可以在参与碰撞的两个小球之间添加一根轻质弹簧，弹簧只与其中一个小球焊接，观察弹簧的形变就可以了解碰撞过程中内力的作用规律(其实，在弹簧弹力作用的时间内，这就是一个复振子系统).如图2所示.他们之间对应的联系如表1所示.碰后1球和2球的速度分别用v′1和v′2表示.

图2 一维碰撞模型分析

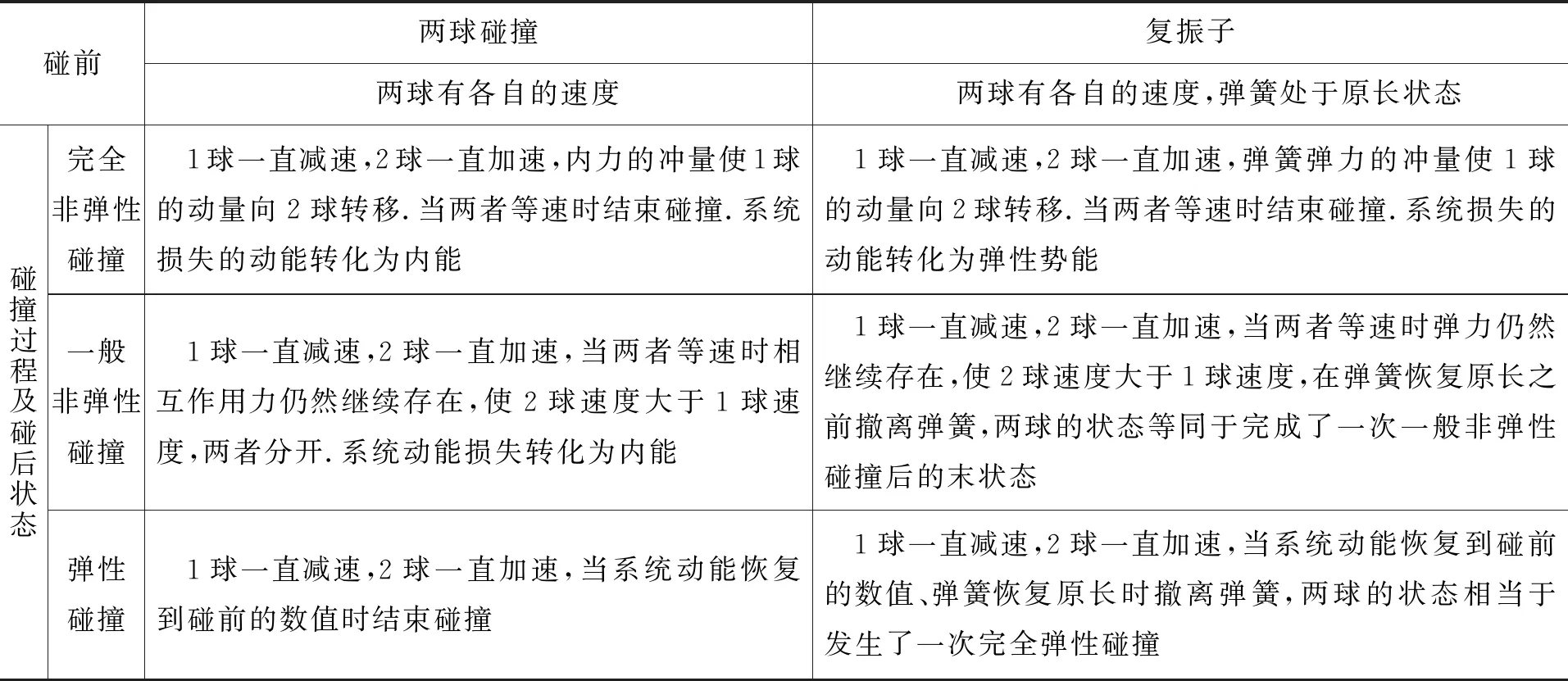
表1 两球碰撞与复振子系统之间的联系

1.1 新情境“新”在何处？

有3个物体参与相互作用，且运动是二维运动.

1.2 新情境中蕴含“旧”规律

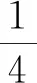
所以，两小球第一次碰前相对速度大小为

原题第(1)问得解.

假设两小球碰后能回到与初始时刻一样的相对大圆环的位置，则小球相对大圆环的速度是x轴方向，大圆环相对大桌面的速度也沿x轴方向，所以系统不存在y轴方向速度，则整个过程相当于一次x轴方向的完全弹性碰撞，代入公式得小球碰后速度

可以看到，若2m>M，则小球相对大桌面的速度朝右，若2m

综上所述，物理有助于我们在新的物理情境中更清晰、快速地找到其内在的物理规律，返璞归真，体会到物理规律的逻辑美.

2 深挖物理内涵 创设各种角度 引领学生做思维训练

笔者不改变题干设定，适当改变设问的方式和角度，启发学生去思考.

(1)小球能否发生第二次、第三次碰撞?

这个问题主要是引导学生探究t=0时刻之后很长一段时间内的运动规律.引导学生去分析为什么大圆环和两小球构成的系统质心会一直做匀速直线运动，而在质心系中两小球每碰撞2次之后，3个物体就会回到与t=0时刻一样的相对位置.可见，在质心系中，三者的运动是周期往复的.

这个问题主要在于引导学生对非弹性碰撞模型和弹性碰撞模型的特点进行比较.

解析：从t=0时刻开始到第一次碰撞前瞬间，x轴方向完成了一次完全非弹性碰撞，如上所述，A,B球碰前的相对速度为

三者的x轴方向达到共速

已知恢复系数，可求碰后相对速度大小为

(3)假设圆环形细管道与A,B小球质量相等均为m，且有两个对称的缺口P1和P2，如图3所示，位置已经由方位角φ标定，A，B球将在缺口处穿出，在大桌面上某处相碰.求相碰时两球与管道中心O之间的距离以及两球从缺口穿出后到小球相碰的过程中圆环形细管道经过的路程[1].

图3 圆环形轨道的两个对称缺口

这个问题旨在引导学生在不同的参考系中观察物体的运动.先以细管为参考系，设小球穿出前的运动看成是随圆环形细管以u的速度的同时相对大圆环做速度为v的圆周运动，A，B球相对大圆环从缺口处穿出后三者都做匀速直线运动，如图4所示.所以，两小球会在Q点碰撞，此时Q与O之间的距离为

图4 两球从缺口处穿出在Q点碰撞

设小球穿出缺口到相碰经历时间t，小球相对管道经过路程为

Rcotφ=vt

接下来我们回到实验室参考系，在上述这段时间内，圆环形细管相对大桌面经过的路程为

又穿出前系统动量守恒、机械能守恒

mu+2m(vcosφ+u)=2mv0

以上就是笔者在实际的物理竞赛培训时对一道习题的处理方式，可操作性强，学生积极性很高，思维训练量大，学生能紧扣物理内在规律，建模能力得到了非常明显的提高.